Карагандинский технический университет имени Абылкаса Сагинова
Кафедра ЭС
Расчетно-графическая работа №2
Дисциплина: Теоретические основы электротехники
Выполнил: студент Сорокина Ю.В
группы:ЭЭ-21-4
Проверил: ст.преподаватель
Биличенко.Е.Н
2022
Расчетно-графическая работа №2
1.Исходные данные для выполнения расчётно-графической работы
Таблица 1
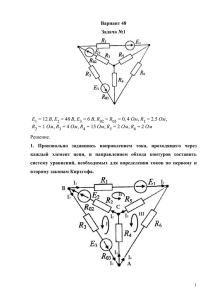
Вариант
39
Вариант
Рису- L1 L2 L3
нок
мГн
1,22
0
0 50
Рисунок
C1
1
C2 C3
мкФ
0
0,4
e'1
R1
R2
R3
25
0
f
Гц
800
Ом
0
e"1
e'2
e"2
e'3
e"3
0
0
705cos(ωt+90˚)
0
В
39
1,22
620sin(ωt+54˚)
538cos(ωt+22˚)
Рисунок 1 - исходная схема
Так как e2'=0, e2''=0, e3''=0, то схему можно упростить, исключив из нее
эти элементы. Для дальнейшей работы выбираем направления обхода
контуров по часовой стрелке.
Рисунок 2-Преобразованная схема
Для определения сопротивлений необходимо найти угловую частоту.
Угловая частота:
𝜔 = 2 ∙ 𝜋 ∙ 𝑓 = 2 ∙ 𝜋 ∙ 800 = 5026,54825
рад
с
Сопротивления реактивных элементов в схеме:
𝑋𝐿3 = 𝜔 ∙ 𝐿3 = 5026,54825 ∙ 50 ∙ 10−3 = 251,327 Ом
𝑋𝐶1 =
𝑋𝐶3 =
1
1
=
= 198,944 Ом
𝜔 ∙ 𝐶1 5026,54825 ∙ 1 ∙ 10−6
1
1
=
= 497,359 Ом
𝜔 ∙ 𝐶3 5026,54825 ∙ 0,4 ∙ 10−6
Задание 1. На основании законов Кирхгофа составить в общем виде
систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух
формах: а) дифференциальной; б) символической.
а) дифференциальная форма
𝑖1 − 𝑖2 + 𝑖3 = 0
1
∫ 𝑖1 𝑑𝑡 + 𝑖2 𝑅2 = 𝑒1′ + 𝑒1′′ .
𝐶1
𝑑𝑖3 1
−𝐿3
− ∫ 𝑖3 𝑑𝑡 − 𝑖2 𝑅2 = −𝑒3′
𝑑𝑡 𝐶3
{
б) символическая форма:
𝑖1 − 𝑖2 + 𝑖3 = 0
{𝑗(−𝑋𝐶1 ) ∙ 𝐼1̇ +𝐼̇ 2 ∙̇ 𝑅2 = 𝑒1′ + 𝑒1′′
−𝑗(−𝑋 ) ∙ 𝐼 − 𝐼 ̇ ∙ 𝑅 = −𝑒 ′
𝐶3
3
2
2
3
Задание 2. Определить комплексы действующих значений токов во всех
ветвях цепи, воспользовавшись одним из методов расчета линейных
электрических цепей.
В первую очередь необходимо от мгновенных значений ЭДС перейти к
комплексам действующих значений ЭДС.
𝑒1′ = 620sin(ωt + 54˚) =>
620𝑒 𝑗54
√2
0
0
≈ 438,4𝑒 𝑗54 ≈ 438,4 ∙ (0,5877 + 𝑗0,809)
= (257,6476 + 𝑗354,6656) В
𝑒1′′
= 538 cos(ωt + 22˚) => 538 sin(ωt + 112˚) =>
538𝑒 −𝑗68
0
√2
≈ 380,42345 ∙ (0,3746 − 𝑗0,9271) = (−142,5066 + 𝑗352,6905)В
𝑒3′ = 705cos(ωt + 90˚)
= 705 sin(ωt + 180) =
705𝑒𝑗180
√2
= −498,51028 B
Комплексные сопротивления ветвей:
0
= 498,51028 ∙ (−1 + 𝑗0)
𝑍1̇ = −𝑗(𝑋𝐶1 ) = −𝑗198,9436 Ом
𝑍2̇ = R2 = 25 Ом
𝑍3̇ = 𝑗(𝑋𝐿3 − 𝑋𝐶3 ) = 𝑗(251,327 − 497,359) = −𝑗246,031 Ом
Комплексные проводимости ветвей:
𝑌1̇ =
1
1
=
= 𝑗0,00502 См
−𝑗198,9436
𝑍1̇
𝑌2̇ =
𝑌3̇ =
1
1
=
= 0,04 См
25
𝑍2̇
1
1
=
= 𝑗0,00406 См
−𝑗246,031
𝑍3̇
По методу двух узлов расчитаем 𝑈𝑓𝑘̇ :
̇ =
𝑈𝑓𝑘
=
(𝐸1′ + 𝐸1′′ ) ∙ 𝑌1̇ + 𝐸 ′ 3 ∙ 𝑌3̇
𝑌1̇ + 𝑌2̇ + 𝑌3̇
((257,6476 + 𝑗354,6656 − 142,5066 + 𝑗352,6905) ∙ 𝑗0,00502) + ((−498,51028) ∙ 𝑗0,00406)
(𝑗0,00502 + 0,04 + 𝑗0,00406)
= −92,34753 − 15,192745𝑗
𝐼1̇ =
=
̇
(𝐸1′ + 𝐸1′′ ) − 𝑈𝑓𝑘
𝑍1̇
(((257,6476 + 𝑗354,6656) + (−142,5066 + 𝑗352,6905))) − (−92,34753 − 15,192745𝑗)
(−𝑗198,9436)
= −3,63215 + 1,043145𝑗
𝐼2̇ =
𝐼3̇ =
̇
𝑈𝑓𝑘
(−92,34753 − 15,192745𝑗)
=
= −3,693901 − 0,60771𝑗
25
𝑍2̇
̇
𝐸 ′ 3 − 𝑈𝑓𝑘
((−498,51028) − (−92,34753 − 15,192745𝑗))
=
(−𝑗246,031)
𝑍3̇
= −0,061751 − 1,650855𝑗
Проверка по первому закону Кирхгофа:
𝑖1 − 𝑖2 + 𝑖3 = 0
(−3,63215 + 1,043145𝑗) − (−3,693901 − 0,60771𝑗)
+ (−0,061751 − 1,650855𝑗) = 0
Задание 3.
По результатам, полученным в пункте 2, определить
показание ваттметра.
𝑃𝑤 = 𝑅𝑒[𝑈𝑤̇ ∙ 𝐼1̇ ]
𝑈𝑤 = 𝐼1̇ ∙ 𝑍1̇ = (−3,63215 + 1,043145𝑗) ∙ (−𝑗198,9436)
= 722,59299 − 207,52702𝑗
𝑃𝑤 = 𝑅𝑒[(722,59299 − 207,52702𝑗) ∙ ((−3,63215 + 1,043145𝑗))]
= 𝑅𝑒[−2624,5661 + 1507,5385𝑗 − 216,48077𝑗 2 ]
= 𝑅𝑒[1291,05773𝑗 − 2624,5661] = −1333,50837 Вт
Задание
4.
Построить
топографическую
диаграмму
напряжений,
совмещенную с векторной диаграммой токов, приняв равным нулю
потенциал точки а.
Рисунок 3 - контур для построения топографической диаграммы
𝜑𝑎̇ = 0.
𝜑𝑓̇ = 𝜑𝑎 + 𝐸 ′1 = (257,6476 + 𝑗354,6656)
𝜑𝑘̇ = 𝜑𝑓 − 𝐼2 ∙ 𝑅2
= (257,6476 + 𝑗354,6656) − (−3,63215 + 1,043145𝑗) ∙ 25
= 167,280018 + 417,632627𝑗
𝜑𝑏̇ = 𝜑𝑘 + 𝐸 ′′1
= (167,280018 + 417,632627𝑗) + (−142,5066 + 𝑗352,6905)
= 24.770886 + 417.632627𝑗
𝜑𝑎 = 𝜑𝑏 + 𝑗𝑋𝐶1 𝐼1
= (24.770886 + 417.632627𝑗)
+ (198,944𝑗 ∙ (−142,5066 + 𝑗352,6905)) ≈ 0 𝐵
Для построения векторной и топографической диаграммы необходимо на
координатной плоскости расположить ось действительных значений (ось
абсцисс) и ось мнимых значений (ось ординат). Нужно учитывать, что
значения тока и потенциалов сильно различаются, в следствии этого
необходимо подобрать масштаб.
В нашем случае масштаб соответствует: I ̇×30, φ ̇:10
Рисунок 4. Топографическая диаграмма напряжений, совмещенная с
векторной диаграммой токов
Задание 5. Построить круговую диаграмму тока в одном из сопротивлений
цепи при изменении модуля этого сопротивления в пределах от нуля до
бесконечности. Сопротивление, подлежащее изменению, показано на схеме
стрелкой.
Расчет
для
построения
круговой
диаграммы
ведем
по
методу
эквивалентного генератора.
Разрываем ветвь с изменяющимся сопротивлением ХC1 и определяем
напряжение в месте разрыва - напряжение холостого хода Uxx.
Рисунок 5 - схема с разрывом во второй ветви
𝑈𝑥𝑥̇ определяем по методу двух узлов при 𝑌1̇ = 0.
(180,7199 + 𝑗85,0657) ∙ (−𝑗0,04169)
𝐸 ′1 ∙ 𝑌1̇ + 𝐸 ′′ 3 ∙ 𝑌3̇
𝐸 ′′ 3 ∙ 𝑌3̇
̇ =
𝑈𝑐𝑑
=
=
(−𝑗0,04169) + (0,01538)
𝑌1̇ + 𝑌2̇ + 𝑌3̇
𝑌2̇ + 𝑌3̇
(−7,5342𝑗 − 3,5463𝑗 2 )
=
0,01538 − 0,04169𝑗
=
(3,5463 − 7,5342𝑗) ∙ (0,01538 + 0,04169𝑗)
(0,01538 − 0,04169𝑗) ∙ (0,01538 + 0,04169𝑗)
=
0,0545 + 0,0319𝑗 + 0,3141 0,3686 + 0,0319𝑗
=
0,000236 + 0,001738
0,001974
= 186,7274 + 16,16𝑗
Сопротивление эквивалентного генератора
𝑍̇экв представляет собой
сопротивление паралельно включенных комплексных сопротивлений 𝑍2̇ и 𝑍3̇ .
𝑍̇экв =
𝑍2̇ ∙ 𝑍3̇
((𝑗23,9828) ∙ 65)
(1558,882𝑗) ∙ (65 − 𝑗23,9828)
=
=
(65 + 𝑗23,9828) (65 + 𝑗23,9828) ∙ (65 − 𝑗23,9828)
𝑍2̇ + 𝑍3̇
=
101327,33𝑗 + 37386,3552 37386,3552 + 101327,33𝑗
=
4225 + 575,1746
4800,1746
= 7,7885 + 21,109𝑗
𝐼кз1
𝑈̇ 𝑥𝑥 (186,7274 + 16,16𝑗)
=
=
̇
(7,7885 + 21,109𝑗)
𝑍экв
=
(186,7274 + 16,16𝑗) ∙ (7,7885 − 21,109𝑗)
(7,7885 + 21,109𝑗) ∙ (7,7885 − 21,109𝑗)
=
1454,3263 − 3815,7665𝑗 + 341,1214
60,6607 + 445,5898
=
1795,4477 − 3815,7665𝑗
= 3,5465 − 7,5373𝑗
506,2505
𝜓 = 𝜓𝐶1 − 𝜓𝑍экв = −90° − 21° = −111°
Рисунок 6. Круговая диаграмма токов.
Задание 6. Полагая, что между двумя любыми индуктивными катушками,
расположенными в разных ветвях заданной схемы, имеется магнитная связь с
взаимной индуктивностью М, составить в общем виде систему уравнений по
законам Кирхгофа для расчета токов во всех ветвях схемы, записав ее в двух
формах: а) дифференциальной, б) символической.
Рисунок 7 - схема для выполнения задания 6
а) дифференциальная форма:
𝑖1 − 𝑖2 + 𝑖3 = 0,
1
𝑑𝑖2
𝑑𝑖3
∫ 𝑖1 𝑑𝑡 + 𝐿2
−𝑀
+ 𝑖2 𝑅2 = 𝑒1′′ + 𝑒1′
𝐶1
𝑑𝑡
𝑑𝑡
𝑑𝑖2
𝑑𝑖3
𝑑𝑖3
𝑑𝑖3 1
𝐿2
−𝑀
+ 𝑖2 𝑅2 + 𝐿3
−𝑀
+ ∫ 𝑖 𝑑𝑡 = 𝑒3′ .
{ 𝑑𝑡
𝑑𝑡
𝑑𝑡
𝑑𝑡 𝐶3 2
б) символическая форма:
𝐼1̇ − 𝐼2̇ + 𝐼3̇ = 0,
̇
𝑗(−𝑋𝐶1 ) ∙ 𝐼1 + [𝑅2 𝑗] ∙ 𝐼2̇ − 𝑗𝑋𝑀 ∙ 𝐼3̇ = 𝐸̇1′ + 𝐸̇1′′
{
[(𝑅2 + 𝑗(𝑋𝐿2 − 𝑋𝑀 )] ∙ 𝐼2 + 𝑗(𝑋𝐿3 − 𝑋̇ 𝐶3 − 𝑋𝑀 ) ∙ 𝐼3̇ = −𝐸3′ .
Вывод: Выводом для данной расчетно-графической работы может
служить то, что я научилась выявлять законы Кирхгофа в символической и
дифференциальной формах, так же изучила метод двух узлов, и в дополнение
научилась составлять векторные и круговые диаграммы токов,