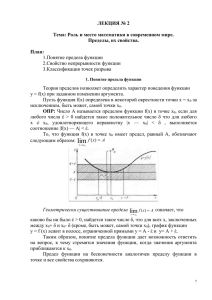
Продолжение. Точки разрыва функции и их классификация.
реклама

ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ Точки , в которыхнарушается непрерывность функции,называются точками разрыва функции. Если х=х0-точка разрыва функции у=f(х),то вней не выполняется по крайней мере одно из условий первого определения непрерывности , а именно: 1.Функция определена в окрестности точки х0, но не определена в самой точке х0 Например,функция у 1 не определена в точке х0=2 х2 2.Функция определена в точке х0 и ее окрестности, но не существует предела f(х) при x x0 . Например, функция : f(х)= х 1, если 1 х 2, 2 х, если 2 х 5, Определена в точке х0=2 (f(2)=0), Однако в точке х0=2 имеет разрыв (см.рисунок) т.к. эта функция не имеет предела при x 2 : lim f ( x) 1, lim f ( x) 0. x 2 0 x 2 0 3.Функция определена в точке х0 и ее окрестности, существует lim f ( x) ,но x x0 f ( x) f ( x0 ) этот предел не равен значению функции в точке х0 : xlim x 0 sin x Например, функция g ( x) , если х 0 x 2, еслих 0 sin x 1, а g(х0)=g(0)=2 (см.рис.) x 0 x Здесь х0=0 – точка разрыва: lim g ( x) lim x 0 Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы),т.е lim f ( x) A1 и lim f ( x) A2 xx0 0 xx0 0 При этом: а) если А1=А2, то точка х0 называется точкой устранимого разрыва б)если A1 A2 то точка х0 называется точкой конечного разрыва Величину A1 A2 называют скачком функции в точке разрыва первого рода. Точка разрыва х0называется точкой разрыва второго рода функции y=f(x),если по крайней мере один из односторонних пределов (слева или справа ) не существует или равен бесконечности. 1.Обратимся к функцииy 1 x2 , х0=2 – точка разрыва второго рода. 2.Для функции f(x)= х 1, если 1 х 2, 2 х, если 2 х 5, Х0=2 – точка разрыва первого рода , скачок функции равен 3. Для функции sin x g ( x) x 2 1 0 1. ,x 0 ,x 0 Х0=0 является точкой устранимого разрыва первого рода. Положив g(x)=1 (вместо g(x)=2) при х=0, разрыв устраниться,функция станет непрерывной. x3 Пример: Дана функция f ( x) x3 Найти точки разрыва,выяснить их тип. Решение: Функция f(x) определена и непрерывна на всей числовой оси,кроме точки х=3. 1 ,x 3 Очевидно ,f(x)= 1 , x 3 Следовательно,lim x30 f ( x) 1, а lim f ( x) 1. x30 Поэтому в точке х=3 функция имеет разрыв первого рода.Скачок функции в этой точке равен 1-(-1)=2.