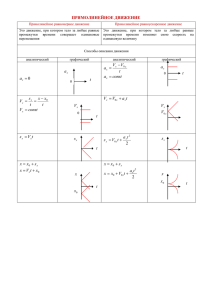
Интегрирование одномерного уравнения движения точки

ДИНАМИКА
ТОЧКИ
ЛЕКЦИЯ 2:
ИНТЕГРИРОВАНИЕ ОДНОМЕРНОГО
УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ
1. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
МАТЕРИАЛЬНОЙ ТОЧКИ
Пусть материальная точка движется вдоль оси x. Тогда во время движения y=z=0.
my  Fy
Fy  0
mz  Fz
Fz  0
необходимые условия
движения по прямой
Эти условия не достаточны! (см. пример)
Для того, чтобы материальная точка двигалась по прямой необходимо и достаточно,
чтобы действующая на нее сила была все время параллельна начальной скорости
движения точки.
Д-во достаточности: Ось x направим по начальной скорости, а начало координат
совместим с начальным положением точки.
Fy  Fz  0
y0
z 0
y  C1 , y  C1t  C3
z  C2 , z  C2t  C4
y (0)  0, y (0)  0
z (0)  0, z (0)  0
C1  C3  0
C2  C4  0
2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ:
РЕШЕНИЯ В КВАДРАТУРАХ
В силу нелинейности дифференциального уравнения,
определение его решения в общем случае возможно только
численно (приближенно).
Однако существуют частные случаи, в которых нахождение
решения уравнения при выполнении начальных условий
сводится к квадратурам – взятию интегралов.
Выделим три таких случая:
F  F (t );
F  F ( x);
F  F ( x)
3. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
F(t)
mx  F (t )
dx 1
 F (t )
dt m
x
x
1
F (t )dt  C1

m
1 
F (t )dt  dt  C1t  C2



m
4. ПРИМЕР: ГАРМОНИЧЕСКИ
ИЗМЕНЯЮЩАЯСЯ СИЛА
mx  F (t )
x(0)  x(0)  0
F (t )  P cos t
F (t )  P sin t
x(t )  
P
sin t  C1t  C2
2
m
x(t )  
P
cos t  C1t  C2
2
m
12
P
m
P
x(t ) 
t  sin t 
m 2
F=P sin( t)
10
C2 
8
2
m  x/P
C2  0, C1 
F=Pcos( t)
6
x(t ) 
4
2
0
0
P
, C1  0
2
m
2
4
t
6
8
10
P
1  cos t 
m 2
5. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
F(x)
mx  F ( x)  x
mxx  F ( x) x
m d  x
mxx 
2 dt
2
F ( x) x 
 x 
2
d
dt
  F ( x)dx 
2
F ( x)dx  C1

m
dx
2

F ( x)dx  C1

dt
m
dt  
t

dx
2
F ( x)dx  C1

m
 C2
dx
2
F ( x)dx  C1

m
t    x; C1 , C2 
x    t; C1 , C2 
6. ПРИМЕР : ПАДЕНИЕ ЗЕМЛИ НА
СОЛНЦЕ
x
x
fM
x2
x(0)  x0
x(0)  0
x0  1.5 1011 м
м3
11
f  6.6 10
кг  с 2
M  2 1030 кг
1 d
fM
d 1
2
x


x

f
M
 
 
2 dt
x2
dt  x 
1 1 
1  dx 
   fM  
2  dt 
 x x0 
2
1 1 
dx
 2f M  
dt
 x x0 

x
dx
x 1  x01
 x
x
x 
2 f M t  x03/ 2 
1   arcsin
 
x0
x0 2 
 x0
1
0.8
0.6
x/x0
t

t0
0.4
0.2
0
0
2 f Mt 
x0
0.5
1
t/t0
1.5
2
x
x
x 
1   arcsin

x0
x0
x0 2
x03
t0 
 42 дня
2f M
t fin 

2
t0  2 мес.
7. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
F(dx/dt)
СПОСОБ 1
vx
mx  F ( x)
x    (t , C1 )dt  C2
mv  F (v )
x   (t , C1 )
dv
dt

F (v ) m
t  ( x, C1 )
dv
t

C

 F (v ) 1 m
СПОСОБ 2
mx  F ( x)
t
x
dv dv dx
dv

v
dt dx dt
dx
dx
 C2
 ( x, C1 )
x   ( x, C1 )
mvdv
 dx
F (v )
x  m
vdv
 C1
F (v )
8. ПРИМЕР: ПАДЕНИЕ ТЕЛА С
КВАДРАТИЧНЫМ СОПРОТИВЛЕНИЕМ
Точка массы m падает на Землю из состояния покоя под действием постоянной
силы тяжести. Найти скорость и закон движения точки, если сила сопротивления
пропорциональна квадрату скорости ( R  k 2 mv 2 , где k — постоянная).
v  g k v
g  kv
1
dv
ln
 t  C1
 dt
2 2
2k g
g  kv
g k v
k gt
 k gt
v (0)  0
d
e

e
1
dt  2
k
ek gt  e  k gt
g e2 k gt  1
g ek gt  e k gt
dx 
dt 
2 k gt
k e
k ek gt  e k gt
1
1
x  2 ln e k gt  e  k gt  C2
k
1
x(0)  0  C2   2 ln 2
k
1
1
 e t / t0  e  t / t 0 
x
x

,
t

 ln 
0
0

k2
k g
x0
2


g
ln 2
Приближенное
t t0  x 
t 2
решение
k
k




2
x/x0
mx  mg  mk 2 x 2
2 2
Exact
Approximation
1
0
-1
0
1
2
t/t0
3
9. БЕЗРАЗМЕРНЫЕ
ПЕРЕМЕННЫЕ
Исходная задача
Единицы измерения
x  g  k 2 x2
x (0)  x(0)  0
x  м t c 
x  cм t  ч 
x  миля  t сут 
g  м c 2  k 2  м-1 
 g см ч 2  k 2 см-1 
 g  миля сут 2  k 2  миля -1 
Численное значение констант g и k зависит от единиц измерения. Нельзя ли
выбрать «родные» для задачи единицы, так, чтобы она стала максимально простой?
t  t t0
x  x x0
dx d  x0 x  x0 d x



dt d  t0 t  t0 d t
d 2 x x0 d 2 x

dt 2 t02 d t 2
2
2
2
d x 
x0 d 2 x
d 2 x t02
2 x0  d x 
2
 2


g

k

g

k
x
0



t0 d t 2
t02  d t 
d t 2 x0
d
t


t02
1
Черточки над x и t для
g  1, k 2 x0  1  x0  k 2 , t0 
x  1  x2
x0
k g
простоты записи опущены
Исходная
задача
10. ПРЕИМУЩЕСТВА
БЕЗРАЗМЕРНЫХ ПЕРЕМЕННЫХ
Проще решать. Не нужно таскать константы,
труднее ошибиться
 Задачу нужно решить лишь один раз, а не для
каждого набора параметров. Все остальное
делается простым растяжением координат x и t
 Свойства изучаемого процесса проще
анализировать если решение есть функция одной
переменной


x  k 2 F k gt

лучше чем
x  F  t, k 2 , g 
11. ПРИМЕР: ПАДЕНИЕ ТЕЛА С
ЛИНЕЙНЫМ СОПРОТИВЛЕНИЕМ
Та же задача, но R  k 2mv , где k — постоянная.
mx  mg  mk 2 x x (0)  x(0)  0
Можно было бы решать как и предыдущую. Но рассматриваемое уравнение имеет
огромное достоинство: оно принадлежит классу линейных диф. уравнений с
постоянными коэффициентами. Метод их решения чрезвычайно прост и общ.
Рассмотрим вначале однородное диф. уравнение второго порядка с постоянными к-ми
x  ax  bx  0
Для построения его общего решения достаточно найти два частных решения.
Если x1 (t )и x2 (t )-такие решения, то в силу линейности C1 x1  C2 x1 -общее решение.
Частные решения легко предъявляются.
x  et  x  ax  bx  et  2  a  b  0    1,2 -корни квадратного ур-ния
Общее решение однородного уравнения
x  C1e1t  C2e2t


Для построения общего решения неоднородного уравнения x  ax  bx  f (t )
достаточно найти какое либо его частное решение x0 (t ) . В силу линейности
t
t
общим решением будет x  x0 (t )  C1e 1  C2e 2 . Общий алгоритм построения x0 (t )
будет дан в курсе ДУ. Но во многих случаях x0 (t ) просто угадывается
12. ПРИМЕР: ПАДЕНИЕ ТЕЛА С
ЛИНЕЙНЫМ СОПРОТИВЛЕНИЕМ
mx  mg  mk 2 x x (0)  x(0)  0
1) Переходим к безразмерным переменным
t  t t0
x0 d 2 x
2 x0 d x
 2

g

k
t0 d t 2
t0 d t
x  x x0
x  x 1
d 2 x t02
2 d x

 g  k t0
d t 2 x0
dt

t0  k  2
x0  gk 4
По-прежнему черточки над x и t для простоты записи опущены
2) Угадывем частное решение
x0 (t )  t
3) Решаем характеристическое уравнение
 2    0  1  0, 1  1
x (t )  x0 (t )  C1e1t  C1e2t  t  C1  C2e  t
4) Выписываем общее решение
5) Находим произвольные константы из начальных условий
x  F (t )  t  1  e  t
6) Выписываем окончательный результат
x
g
F ( k 2t )
4
k