Графический метод

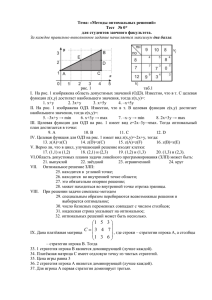
Графический метод.
I. Дана целевая функция некоторой задачи линейного программирования f(x)= c0 +c1 x1+
c2 x2. Верно утверждение:
1. если c0=3, c1=5, c2= – 3, то в направлении вектора i  2 j функция f(x) убывает
2. если c0= – 5, c1=18, c2= 19, то в направлении вектора 7i  6 j функция f(x) возрастает
быстрее всего
3. если c0=1, c1= – 3, c2=2, то в направлении вектора 6i  9 j функция f(x) не изменяется
4. если c0= – 5, c1=4, c2= – 3, то в линии уровня функции f(x) параллельны вектору
5i  4 j .
II. Пусть имеется целевая функция f(x) некоторой задачи линейного программирования.
Верно утверждение:
51. если grad f ( x)  21i  17 j , то приращение Δf(x), соответствующее приращениям
переменных Δx1 = – 3 и Δx2 = – 4, меньше нуля
6. если grad f ( x)  45i  27 j , то линии уровня функции f(x) перпендикулярны
прямой 3x1 + 5x2 – 1=0
7. если grad f ( x)  12i  17 j , то в направлении вектора 2i  3 j приращение функции
Δf(x)=0
8. если grad f ( x)  18i  24 j , то в направлении вектора 3i  4 j скорость
возрастания функции f(x) наибольшая
III. На рис. изображена область допустимых значений (ОДЗ). Известно, что в т. C целевая
функция z(x,y) достигает наибольшего значения, тогда z(x,y)=
9. x
10. x-y
11. y
12. -2x+y
IV. На рис. изображена ОДЗ. Известно, что в т. A целевая функция z(x,y) достигает
оптимального значения, тогда z(x,y)=
13. 4y → min 14. 3x+2y → min
15. x+y → max
16. x-4y → max
V. Целевая функция для ОДЗ на рис. 1 имеет вид z=y→min. Тогда оптимальный план
достигается в точке:
17. F
18. B
VI. Целевая функция для ОДЗ на рис. 1 имеет вид z(x,y)=-3y, тогда:
19. z(A)=z(F)
20. z(D)<z(A)
21. z(A)=z(B)
22. z(B)>z(E)