Графический метод

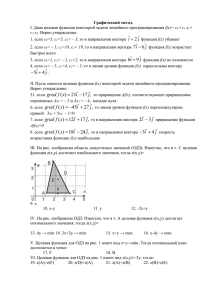
I. Дана целевая функция некоторой задачи линейного программирования f(x)= c0 +c1 x1+
c2 x2. Верно утверждение:
1. если c0=3, c1=5, c2= – 3, то в направлении вектора i  2 j функция f(x) убывает
2. если c0= – 5, c1=18, c2= 19, то в направлении вектора 7i  6 j функция f(x) возрастает
быстрее всего
3. если c0=1, c1= – 3, c2=2, то в направлении вектора 6i  9 j функция f(x) не изменяется
4. если c0= – 5, c1=4, c2= – 3, то в линии уровня функции f(x) параллельны вектору
5i  4 j .
II. Пусть имеется целевая функция f(x) некоторой задачи линейного программирования.
Верно утверждение:
5. если grad f ( x)  21i  17 j , то приращение Δf(x), соответствующее приращениям
переменных Δx1 = – 3 и Δx2 = – 4, меньше нуля
6. если grad f ( x)  45i  27 j , то линии уровня функции f(x) перпендикулярны
прямой 3x1 + 5x2 – 1=0
7. если grad f ( x)  12i  17 j , то в направлении вектора 2i  3 j приращение функции
Δf(x)=0
8. если grad f ( x)  18i  24 j , то в направлении вектора 3i  4 j скорость
возрастания функции f(x) наибольшая
III. На рис. изображена область допустимых значений (ОДЗ). Известно, что в т. C целевая
функция z(x,y) достигает наибольшего значения, тогда f(x,y)=
9. x
10. x-y
11. y
12. -2x+y
IV. На рис. изображена ОДЗ. Известно, что в т. A целевая функция f(x,y) достигает
оптимального значения, тогда f(x,y)=
13. 4y → min 14. 3x+2y → min
15. x+y → max
16. x-4y → max
V. Целевая функция для ОДЗ на рис. 1 имеет вид z=y→min. Тогда оптимальный план
достигается в точке:
17. F
18. B
VI. Целевая функция для ОДЗ на рис. 1 имеет вид f(x,y)=-3y, тогда:
19. f(A)=z(F)
20. f(D)<z(A)
21. f(A)=z(B)
22. f(B)>z(E)
VII. Дана система ограничений и целевая функция:
ìï 8x + 2x - 23 ³ 0
2
ïï 1
ïï
ïï 3x 1 - 10x 2 + 29 ³ 0
ï 2x - x - 9 £ 0
, f (x ) = c 0 + c1x 1 + c2x 2
í 1
2
ïï
ïï 6x 1 + 8x 2 - 27 ³ 0
ïï
ïï x 1, x 2 ³ 0
ïî
23. план x=(7;5) может быть точкой минимума при некотором выборе коэффициентов
целевой функции f(x)
24. планы x=(2;7/2) и x=(5;1) одновременно могут быть оптимальными при некотором
выборе коэффициентов целевой функции f(x)
25. план x=(11/3;4) является единственной точкой максимума при некотором выборе
коэффициентов целевой функции f(x).
VIII. Задана симплекс-таблица некоторой задачи линейного программирования:
баз. x1 x2 x3 x4 x5 x6 b0
1
0
-2 4
2
0
16
0
0
2
7
5
1
d
0
1
3
-3 3
0
9
f(x) 0
0
a
b
c
0
4
таб. 1
26. Если a, b, c положительны, то решение оптимально.
27. Если d = 0, то решение вырождено.
Часть II
Задана симплекс-таблица некоторой задачи линейного программирования
баз. x1 x2 x3 x4 x5 x6 b0
1
0
-2 4
2
0
16
0
0
2
7
5
1
8
0
1
3
-3 3
0
9
f(x) 0
0
3
6
-5 0
4
таб. 2
1. Укажите изменение целевой функции таб. 2 после её улучшения:
А).
Б).
В).
Г).
2. В таб. указана ЗЛП, тогда базисными переменными являются:
А). x2, x6, x1
Б). x2, x5, x3
В). x1,x2, x3
С). x6, x5, x4
3. Если в базис ввести x5, то значение целевой функции
А). увеличится
Б). уменьшится
В). не изменится
Г). эту переменную вводит в базис нельзя
Часть III.
I. 1. Дана задача линейного программирования. Необходимо
ïìï 2x 1 + x 2 ³ 2
ïï
ï x2 £ 3
f (x 1, x 2 ) = 2x 1 + 8x 2 ® max, ïí
ïï 4x 1 + 3x 2 £ 12
ïï
ïï x 1, x 2 ³ 0
î
решить графическим методом. В ответ укажите оптимальное значение целевой функции.
II. Решить симплекс-методом задачу линейного программирования:
ïìï 2x 1 + x 2 ³ 2
ïï
ï x 2 + 2x 3 £ 6
f (x 1, x 2 , x 3 ) = 2x 1 + 3x 2 + 5x 3 ® max, ïí
ïï 4x 1 + 3x 2 + x 3 £ 12
ïï
ïï x 1, x 2 , x 3 ³ 0
î
2. Вычислить максимальное значение f(x1, x2, x3)
3. Вычислить сумму компонент оптимального плана.
Важно! Экзаменационный тест может отличаться от предлагаемого как по содержанию,
так и по и по количеству задач.