Нормальные напряжения при изгибе

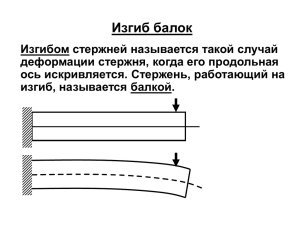
Нормальные напряжения при изгибе
В теории плоского изгиба, для упрощения решения задачи определения
нормальных напряжений, на основании натурных испытаний, приняты
следующие допущения:
•При изгибе продольные сечения балки искривляются по дуге окружности;
•Поперечные сечения плоские до изгиба, остаются плоскими и после изгиба;
•Поперечные сечения пересекаются с продольными волокнами под прямым
углом.
Задача определения нормальных напряжений при изгибе является
статически неопределимой и для ее решения необходимо рассмотреть три
стороны задачи
Статическая (ССЗ)
Геометрическая (ГСЗ)
Физическая (ФСЗ)
Синтез
Статическая сторона задачи
2 участок
1 участок
а
l
 m F   F a  l   R l  Fa  0
 mB Fк   F (a  l )  RAlB  Fa  0
a
RB
RA
F
z1
Опорные реакции
3 участок
A
к
B
F a  l   Fa
F a  l   Fa
 F RB 
F
l
F
l
Проверка  Fкy  F  RA  RB  F  F  F  F  F  0
RA 
Эпюры поперечных сил и изгибающих моментов
z2
1 участок 0 ≤ z1 ≥ a
z3
Q1  F
M1  F  z1 При z1=0, М1(0)=0
При z1=а, М1(а)=F·a
2 участок a ≤ z2 ≥ (a+l) Q2  F  RA  F  F  0
Эпюра поперечных сил
F
M 2  F  z2  F z2  a При z2=а, М2(а)=F·a
При z2=а+l, М2(а+l)=F·(a+l) -F(a+l-a)=Fa
Эпюра изгибающих моментов
Fa

Fa
F
3 участок (a+l) ≤ z3 ≥ (2a+l)
Q3  F  RA  RB  F  F  F   F
M 3  F  z3  F z3  a   F z3  a  l 
При z3=а+l, М3(а+l)=F·(a+l) -F(a+l-a)=Fa
При z3=2а+l, М2(2а+l)=F·(2a+l) -F(2a+l-a)=0
Статическая сторона задачи
Если к балке приложен положительный изгибающий момент, то в этом случае, верхние
ее волокна укорачиваются, а нижние удлиняются. Длина нейтрального волокна
остается неизменной.
Нейтральный слой
RB
F
x
y
RA
F
y
Нейтральный линия
dA
z
Совокупность волокон, не меняющих своей
длины при изгибе балки, называется
нейтральным слоем.
Линия, по которой поперечное сечение
балки пересекается с нейтральным слоем
балки, называется нейтральной линией
сечения.
Qy    dA  0
A
M x   s  y  dA  0
A
x
s
Нейтральный слой
Мx
M y   s  x  dA  0
A
Геометрическая сторона задачи
Длина отрезка на нейтральном слое
Центр
изгиба
a0b0  dz  
Длина отрезка на слое удаленном от нейтрального
на расстояние y
a1b1    y 
Удлинение отрезка после деформации


 ab  a1b1  a0b0    y     y
Относительная деформация
dz
F
a0
a1
b0
b1
F
y
a1b1  a0 b0 y


a0 b0

Физическая сторона задачи
При чистом изгибе в поперечных сечениях балки действуют единственный силовой
фактор изгибающий момент, поперечные силы отсутствуют, а следовательно
отсутствуют и касательные напряжения.
Под действием нормальных напряжений часть волокон балки удлиняется, другая
часть укорачивается и для них можно записать закон Гука при растяжении
a1b1  a0 b0 y


a0 b0

sс
y
x
sр
Нейтральная линия
s  E
s E
y

y
2
Синтез
dA  I x
M x   sydA  
A
Осевой момент
инерции
ССЗ
A
A
ФСЗ

y dA 
2
M x   s  y  dA  0
A
1
ГСЗ
E
a b a b
y
 11 0 0 
a0 b0

s  E
s E
y


s
Ey

E


y 2 dA
A
Mx 
E

M x  EI x
Ix
s
Ey
Mx
s
Ix y
Нормальные напряжения при изгибе
Величина момента инерции характеризует влияние размеров и формы поперечного
сечения балки на ее способность сопротивляться деформации (искривлению).