Лекция 9-12

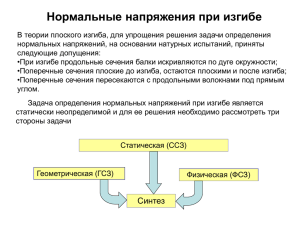
Лекция 9
ИЗГИБ
Общее понятие о деформации изгиба. Типы опор и
балок
1
В настоящей главе рассмотрим деформацию прямого
изгиба стержней, имеющих продольную плоскость
симметрии и прямую ось. Если к прямому стержню
приложить силы, направленные перпендикулярно к его
оси, (или пары сил) так, чтобы их плоскость действия
(силовая .плоскость) совпадала с плоскостью симметрии,
то стержень будет испытывать прямой изгиб (рис. 60, а).
рис. 60
2
При растяжении, сжатии и кручении прямых стержней их
оси сохраняют свою прямолинейную форму. В отличие от этих
видов деформаций изгиб является такой деформацией, при
которой ось прямого стержня теряет свою прямолинейную
формуй делается изогнутой (рис. 60,6). В результате волокна,
параллельные оси, у вогнутой стороны укорачиваются, а у
выпуклой удлиняются. Так как по условию силовая плоскость
совпадает с плоскостью симметрии, то изгиб оси стержня
будет происходить в этой плоскости, т. е. изогнутая ось будет
представлять собой плоскую кривую, лежащую в плоскости
действия сил. Поэтому изгиб называют прямым (см.рис. 60, б).
Стержни, испытывающие деформацию изгиба, называют
балками. Балки являются наиболее часто встречающимися
элементами конструкции. Они воспринимают усилия от одних
элементов и передают их другим. Все внешние силы,
действующие на балки, можно разделить на заданные нагрузки
и их уравновешивающие реакции опор, которые обычно
неизвестны. Заданные нагрузки приводят к сосредоточенным
силам, парам сил и нагрузкам, распределенным по длине
балки.
3
Для выяснения характера реактивных усилий, возникающих
в связях опорных закреплений, рассмотрим основные типы
опор. Наиболее распространены опоры следующих трех
типов: шарнирно-подвижные, шарнирно-неподвижные и
защемление (рис. 61 а, б, в).
рис. 61
4
Шарнирно-подвижная опора (см. рис. 61, а) препятствует
перемещению конца балки в поперечном направлении и
допускает свободный поворот вокруг шарнира опоры и
свободное перемещение вдоль оси.Реакция Ra такой опоры
представляет собой силу, лежащую в плоскости действия
заданных сил и проходящую через центр шарнира
перпендикулярно к оси балки.
5
Шарнирно-неподвижная опора (см. рис. 61, б)
препятствует перемещениям в поперечном и продольном
направлениях и допускает свободный поворот вокруг
шарнира опоры. В этом случае реакцию опоры, лежащую в
плоскости действия заданных сил и проходящую через
центр шарнира, разлагают на две составляющие: Rа —
направленную перпендикулярно к оси, и Hа —
направленную вдоль оси.
При защемлении конец балки (см. рис. 61, в) не может ни
перемещаться, ни поворачиваться в плоскости действия
внешних сил.. В этом случае со стороны опоры на
защемленный конец могут действовать три реактивных
усилия: Ra —сила, направленная перпендикулярно к оси, Hа
—сила, направленная вдоль оси, и момент Мa. Все эти
реактивные усилия уравновешивают заданные нагрузки, а
следовательно, лежат с ними в одной плоскости
В зависимости от типа опор балки разделяют на
консольные и двухопорные
6
Консольной называют балку, у которой один конец защемлен,
а другой свободен (см. рис. 61, г). Двухопорной или
однопролетной называют балку, у которой один конец имеет
шарнирно-неподвижную, а другой — шарнирно-подвижную
опору (см. рис. 61, д).
Если у двухопорной балки одну из опор или обе сдвинуть к
середине (см. рис. 61, е, ж), то у нее появятся
свешивающиеся концы, называемые консолями, сама же
балка в таком случае будет называться соответственно
двухопорной балкой с одной или двумя консолями.
Расстояние между опорами обычно называют пролетом
балки, а длину консольного конца — вылетом консоли
7
Определение поперечной силы и изгибающего
момента
Рассмотрим двухопорную балку, нагруженную в плоскости
симметрии так, как это показано на рис. 62, а. Неизвестные
реакции опор Ra, Ha и Rв могут быть определены из
уравнений статики. При этом реакция Ha=0, так как все
заданные силы перпендикулярны к оси балки.
Чтобы определить внутренние усилия, возникающие в
каком-либо поперечном сечении рассматриваемой балки,
используем метод сечений. Для этого плоскостью А,
проходящей через выбранное сечение, мысленно рассекаем
балку на две части—I и II (см. рис. 62, б) и отбрасываем одну
из них, например, вторую. Так как оставшаяся первая часть
ранее находилась в состоянии равновесия, то для сохранения
этого равновесия при плоской системе сил к сечению
необходимо приложить поперечную силу Q и изгибающий
момент Му (см. рис. 62, в), которые заменят собой действие
отброшенной части. В дальнейшем изгибающий момент Му
будем обозначать Ми.
8
Из третьего уравнения системы (1) поперечная сила,
возникающая в каком-либо сечении,
Q   пр z P
т. е. численно равна алгебраической сумме проекций всех
внешних сил, действующих на рассматриваемую часть
стержня, на ось z.
При изгибе внешние силы, действующие на
рассматриваемую часть балки, параллельны оси z и их
проекции на нее численно равны самим силам, поэтому
поперечная сила будет численно равна алгебраической
сумме этих сил
Q   P
9
При этом условимся считать поперечную силу положительной
от внешней силы. вызывающей сдвиг вверх, если
рассматривается левая часть балки, и вниз, если — правая и
отрицательной от внешней силы, вызывающей
противоположные сдвиги. В этом случае вектор для
положительной силы Q совпадает с направлением внешней
нормали к сечению, повернутой на 90о по часовой стрелке, для
отрицательной — против часовой стрелки.
рис. 62 а
10
рис. 62 б
11
рис. 62 в
12
Из пятого уравнения системы (1) изгибающий момент,
возникающий в каком-либо сечении,
M y  M И   m y P
т. е. численно равен алгебраической сумме моментов всех
внешних сил, действующих на рассматриваемую часть
стержня, относительно оси у.
При изгибе внешние силы, действующие на
рассматриваемую часть балки, лежат в продольной
плоскости симметрии, а ось у перпендикулярна к ней и
проходит через центр тяжести сечения, поэтому
изгибающий момент будет численно равен алгебраической
сумме моментов этих сил относительно центра тяжести
(точки О) взятого сечения.
M И   m0 P 
13
рис. 63 а,б
14
рис. 63 в,г
15
При этом условимся считать изгибающий момент
положительным ют момента внешней силы, изгибающей
рассматриваемую часть балки относительно взятого сечения
выпуклостью вниз, и отрицательным — выпуклостью вверх—
правило дождя — (см. рис. 63, в и г). В таком случае вектор для
положительного момента Mи будет проходить перпендикулярно
плоскости действия сил и направлен к нам, при рассмотрении
левой части, и от нас, при рассмотрении правой части балки.
С целью удобства определения направления изгиба, который
вызывает та или иная нагрузка, рекомендуется мысленно
защемить рассматриваемую часть балки со стороны взятого
сечения, а действие опор заменить реакциями.
В общем случае поперечная сила и изгибающий момент зависят
от положения сечения по длине балки и будут функциями от
абсциссы х. :т. е.
Q  f1 x 
M И  f 2 x 
16
Лекция 11
Эпюры поперечных сил к изгибающих
моментов
При изгибе характер изменения Q и Ми по длине балки
обычно изображают в виде эпюр поперечных сил и
изгибающих моментов. Эпюра поперечных сил — это
графическое изображение закона изменения величины
поперечной силы по длине балки. Ординаты этой эпюры
Q в выбранном масштабе выражают величины
поперечных сил в соответствующих поперечных
сечениях балки.
17
Эпюра изгибающих моментов — это графическое изображение
закона изменения величины изгибающего момента по длине
балки. Ординаты эпюры Ми в выбранном масштабе выражают
величины изгибающих моментов в соответствующих
поперечных сечениях балки
рис. 64
18
рис. 64
19
При построении эпюр поперечных сил и изгибающих
моментов балку разбивают на отдельные участки, в
пределах которых функции Q и Mи и непрерывны.
Границами таких участков являются характерные сечения,
которые совпадают с местами приложения
сосредоточенных сил, пар сил, начала и конца действия
распределенной нагрузки и концами балки. Ось эпюры
обычно располагают параллельно оси балки и на нее сносят
характерные сечения. Условимся на эпюре поперечных сил
ординаты положительных Q откладывать вверх, а
отрицательных— вниз. Что касается эпюры изгибающих
моментов, то здесь, наоборот, ординаты положительных Ми
будем откладывать вниз, а отрицательных—вверх. При этом
эпюра Ми оказывается со стороны растянутых волокон.
20
Рассмотрим построение эпюр поперечных сил и
изгибающих моментов для балки АВ, лежащей на двух
шарнирных опорах и нагруженной силой Р в точке С (рис.
64, а).
Со стороны опор А и В на балку действуют неизвестные
реакции Ra и Rв, которые определяют из уравнений
равновесия. При составлении уравнений равновесия
используют приемы и правила теоретической. механики.
Так, для определения неизвестных реакций Ra и Rв составим уравнения моментов относительно точек А и В (рис.
64, а)
 R A l  Pb  0
 M B  0,
M
A
 0,
RB l  Pa  0
откуда неизвестные реакции
RB 
Pa
l
RA 
Pb
l
21
Проверка полученных результатов
Y  0;
RA  RB  P  P
b  a   P  0
l
Следовательно, реакции Ra и Rв определены верно. Такую
проверку нужно производить всегда, так как ошибка в
определении реакции неизбежно поведет к ошибкам и в
построении эпюр.
Теперь можно приступить к построению эпюр. Как видно из
рис. 64, а, балка АВ имеет два участка: I—АС=а и II—СВ=b, в
пределах которых Q и Ми непрерывные функции х. Построение
эпюр будем производить последовательно по участкам, причем
сначала для Q, а затем для Ми.
В поперечном сечении 1—1 первого участка на некотором
расстоянии х1 от конца А (см. рис. 64, а) при рассмотрении левой
части балки поперечная сила
Qx1   R A 
Pb
l
22
Здесь реакция Ra принята с плюсом, так как вызывает
сдвиг вверх. Выражение для Q(x1) справедливо при
О ≤ х1 ≤ а. Таким образом, в любом поперечном сечении от
A до С поперечная сила постоянна и равна Pb
l
Поэтому эпюра Q ограничена прямой, параллельной оси
(см.рис. 64, б). Следует заметить, что и знак и величина
поперечной силы останутся теми же, если вместо левой
рассмотреть правую часть балки. Действительно, в этом
случае
Pa
 l  a  Pb
Q x1    RB  P  
 P  P

l
l
 l 
23
Здесь реакция Rв, вызывающая сдвиг вверх, принята с
минусом, а сила Р, вызывающая сдвиг вниз—с плюсом, так
как рассматривается правая часть балки. Таким образом,
при определении поперечных сил можно рассматривать
любую часть балки. Обычно рассматривают ту, к которой
приложено меньше сил. Это позволяет получить более
простое выражение для Q.
В поперечном сечении 2—2 второго участка на
некотором расстоянии x2 от С (см. рис. 64, а) при
рассмотрении левой части балки поперечная сила
Pa
a
bl 
Q x 2   R A  P  
 P  P
  P
l
l
 l 
24
Здесь сила Р принята с минусом, так как она в отличие от
реакции Ra вызывает сдвиг вниз. Выражение для Q(х1)
справедливо при О ≤ х2 ≤ b. Таким образом, в любом
поперечном сечении от С до В поперечная сила постоянная
Pb
равна  . Следовательно, эпюра Q для второго участка
l
будет расположена под осью и ограничена прямой, ей
параллельной. Как видно из рис. 64, б, в точке,
соответствующей характерному сечению балки под силой Р,
на эпюре поперечных сил получается скачок, равный в
принятом масштабе внешней силе Р. Такие скачки будут
всегда в местах, соответствующих сечениям балки с
внешними сосредоточенными силами.
В поперечном сечении 1—1 участка АС (см. рис. 64, а)
при рассмотрении левой части балки изгибающий момент
M И  x1   R A x1 
Pb
x1
l
25
Момент инерции Ra относительно центра тяжести сечения
1—1, равный Raх1, принят с плюсом, так как Ra стремится
выгнуть эту часть балки относительно сечения 1—1
выпуклостью вниз. Выражение для Ми (x1) справедливо
при О ≤ х1 ≤ a. Таким образом, на участке от А до С изгибающий момент изменяется по закону прямой
Pbа
линии. Причем Ми (х1=0)=0, а Ми (х1=а)=
l
Следовательно, эпюра Ми будет расположена под осью
(ординаты для положительных Ми откладываем вниз) и
ограничена прямой наклонной линией с ординатой в точке
под сечением А, равной нулю, и в точке под сечением С,
Pbа
равной в принятом масштабе
(см. рис. 64, в).
l
Если вместо левой рассмотреть правую
Pa
l  x1   Pa  x1 
M И  x1   RB l  x1   Pa  x1  
l
26
Здесь момент реакции Rв относительно центра тяжести
сачення 1—1 равный Rв (ι—х1), принят с плюсом, а силы Р,
равный Р(а—x1),—с минусом, так как Rв относительно
сечения 1—1 стремится изогнуть рассматриваемую часть
балки выпуклостью вниз, а Р—выпуклостью вверх.
Pa
Pb
Преобразовывая, получим M И x1   l  x1   Pa  x1   x1
l
l
т. е. и знак и величина изгибающего момента остаются
теми же, если вместо левой рассматривать правую часть
балки. Поэтому при составлении выражения для Ми
обычно рассматривают ту часть балки, на которую
действует меньше внешних сил.
В поперечном сечении 2—2 участка СВ (см. рис. 64, а) при
рассмотрении левой части балки изгибающий момент
M И  x 2   R A a  x 2   Px2 
Pb
a  x2   Px2
l
27
В этом выражении момент реакции Ra относительно
центра тяжести сечения 2—2, равный Ra(a+x2), принят с
плюсом, а силы Р, равный Рх2.—с минусом, так как Ra
стремится изогнуть рассматриваемую часть балки
относительно сечения 2—2 выпуклостью вниз, а Р— выпуклостью вверх. Выражение для Ми(х2) справедливо при
О ≤ х2 ≤ b. Таким образом, на участке балки от С до В
изгибающий момент изменяется по закону прямой линии.
При этом
Pba
M И x2  0 
l
Pb
a  b   Pb  0
M И x2  b  
l
28
Следовательно, эпюра Mи будет расположена под осью и
ограничена прямой наклонной линией с ординатой в точке
Pba
под сечением С, равной в принятом масштабе
(см.
l
рис. 64, в).
Как видно из рис. 64, в, эпюра изгибающих моментов
представляет собой треугольник с вершиной под сечением,
где приложена внешняя сила Р.
Эпюры Q и Mи, изображенные на рис. 64, б, в, дают
наглядную картину распределения поперечных сил и
изгибающих моментов по длине балки и позволяют указать
те поперечные сечения, в которых Q и Ми имеют
наибольшие по абсолютной величине значения. У
призматических балок такие сечения называют опасными.
29
Лекция 11
Определение напряжений при чистом изгибе
При чистом изгибе в поперечных сечениях балки возникает
только постоянный изгибающий момент Ми, который
является равнодействующим моментом внутренних усилий,
распределенных по всему поперечному сечению. Чтобы
выяснить вид и закон распределения внутренних усилий,
рассмотрим чистый изгиб балки, один конец которой
защемлен, а к другому приложена пара сил с моментом М
(рис. 67, а). Нанесем на поверхности балки до ее деформации
две поперечные риски 1—1 и 2—2, представляющие собой
следы поперечных сечений (см. рис. 67, б), и между ними две
продольные риски а—b и с—d, изображающие продольные
волокна. Первая риска расположена близко к верхнему, а вторая близко к нижнему краю. Очевидно, до деформации
аb=сd.
30
Опыт показывает, что после изгиба под действием момента
М (см. рис. 67, в) поперечные риски 1—1 и 2—2, оставаясь
прямыми и сохраняя свое нормальное положение к
продольным волокнам, повернутся вокруг некоторых осей,
проходящих через точки Q1 и Q2, и займут положение 1'— 1'
и 2'— 2', образуя между собой некоторый угол ∆Ө . Из этого
можно сделать вывод, что не только риски 1—1 и 2—2
(следы сечений), а и сами сечения, оставаясь плоскими
(гипотеза плоских сечений) и нормальными к продольным
волокнам, поворачиваются вокруг тех же осей, одно
относительно другого па угол ∆Ө.
31
Риски а—b и с—d, представляющие собой соответственно
верхние и нижние продольные волокна между сечениями
1—1 и 2—2, после деформации займут положения a1—b1 и
c1—d1. При этом отрезок a1b1 будет меньше ab, а c1d1 больше
cd, т. е. верхние волокна получают укорочения, а нижние —
удлинения. На некотором уровне между волокнами a1—b1 и
c1—d1 находятся волокна, которые не получают ни
укорочения, ни удлинения, их длина остается неизменной.
Слой волокон, не изменяющих своей длины, называют
нейтральным слоем балки. По одну сторону от нейтрального
слоя имеет место укорочение волокон, а по другую —
удлинение. Каждое поперечное сечение балки пересекается с
нейтральным слоем по прямой, которую называют
нейтральной линией сечения.
32
рис. 67
33
Так как изменение длин волокон происходит за счет поворота
поперечных сечений, то, очевидно, волокна, проходящие
через их оси вращений (на рис. 67, в—это О1, О2), образуют
нейтральный слон, а следовательно, нейтральные линии
будут являться осями поворотов поперечных сечений. Балка
симметрична относительно плоскости действия сил, поэтому
ее деформация будет симметрична относительно этой
плоскости. Отсюда следует, что удлинение (укорочение)
волокон не зависит от их положения по ширине балки, а
нейтральные линии как линии, через которые проходят
волокна с одинаковой нулевой деформацией, будут
перпендикулярны к плоскости действия сил.
34
Таким образом, деформацию чистого изгиба можно
рассматривать как взаимный поворот поперечных сечений
вокруг нейтральных линий, перпендикулярных к плоскости
действия сил, сами же сечения остаются плоскими и
нормальными к продольным волокнам.
Рассмотрим элемент балки длиной dx, заключенный
между некоторыми поперечными сечениями т—т и n—n
(рис. 68, о). В этом элементе на некотором расстоянии z—а
от нейтрального слоя (здесь а— расстояние от нейтральной
линии до оси у, проведенной через центр тяжести сечения)
выделим элементарное продольное волоконо е—f (см. рис.
68, а).
35
рис. 68 а,б
36
рис. 68 в,г
37
При деформации чистого изгиба под действием изгибающих
моментов Ми поперечные сечения т—т и п—п, оставаясь
плоскими и нормальными к продольным волокнам, повернутся
вокруг своих нейтральных линий 0101 и 0202 на угол ∆Ө (см. рис.
68, б). В результате все продольные волокна между сечениями т—
т и n—n, расположенные ниже нейтрального слоя, в том числе и
волокно е—f, получат удлинения, а выше—укорочения. Волокна
же нейтрального слоя, сохраняя свою длину, только изогнутся по
дуге радиуса ρ. Предполагают, что при чистом изгибе между
продольными волокнами нет сил взаимодействия, поэтому
волокно е—f испытывает деформацию растяжения и его можно
уподобить элементарному призматическому стержню длиной dх,
площадью поперечного сечения dF , к концам которого
приложены только растягивающие элементарные силы dN (см.
рис. 68, б). Следовательно, в точках е и f поперечных сечений т—
т и n—п будут возникать только нормальные напряжения
dN
 
dF
38
Волокно е—f и сечения т—т и п—п взяты произвольно,
поэтому во всех точках любого поперечного сечения балки
(исключая точки по нейтральным линиям) при чистом
изгибе возникают только нормальные напряжения σ.
На основании закона Гука нормальные напряжения в
точках е и f поперечных сечений т—т и п—п будут,
  E
где ε—продольная деформация волокна е—f.
Если до деформации волокно е—f имело длину dх, то
после деформации (см. рис. 68, б) его
e1 f1   p  z  ad
39
Волокна нейтрального слоя после деформации имеют
форму дуги длиной
dx  d
Следовательно, начальная длина волокна е—f
ef  dx  d
Тогда продольная деформация волокна е—f
e1 f 1  ef    z  a d  d z  a



ef
d

(223)
Подставляя значение ε в выражение для σ, получим
 E
za

(224)
40
Так как сечения т—т и п—п и волокно е—f взяты
произвольно, то выражение (224) будет справедливо для
любой точки любого поперечного сечения. Чтобы
воспользоваться формулой (224), необходимо знать
величину а, т. е. знать, как проходит нейтральная линия по
высоте сечения.
При чистом изгибе в поперечных сечениях балки
нормальная сила
N  dN  0

F
Подставляя значение dN = σdF с учетом выражения
(224), получим

z  a
E
E
F dN  F E  dF   F zdF   a F dF  0
откуда
a
 zdF
F
 dF
F
(225)
41
Здесь dF  F — площадь сечения, а  zdF  S y—статический

F
F
момент относительно оси у. Статический момент Sу=0, так
как ось у проходит через центр тяжести сечения.
Следовательно, а=0, т. e. нейтральная линия проходит через
центр тяжести сечения и совпадает с осью у. При а=0,
выражение (224) приобретает следующий вид
 E
z

Таким образом, при чистом изгибе нормальные
напряжения σ в какой-либо точке поперечного сечения
балки прямо пропорциональны расстоянию z этой точки до
нейтральной линии, проходящей через центр тяжести
сечения. Нормальные напряжения, как и деформации
волокон, не зависят от положения точек по ширине сечения
42
Зная закон распределения нормальных напряжений и
изгибающий момент Ми для некоторого поперечного
сечения, можно определить величину нормальных
напряжений σ. Как видно из рис. 68, б, момент элементарной
силы dN = σdF относительно оси у будет
dM И  zdN  zdF
Тогда изгибающий момент
M И   dM И   zdF
F
F
Или с учетом (226)
MИ  E
F
z2

dF 
E

2
z
 dF
F
43
Лекция 12
Подставляя полученное выражение кривизны в (226),
получим формулу для определения нормальных
напряжений в любой точке поперечного сечения балки
MИz
(228)

Iy
Наибольшие нормальные напряжения при z = zmax
 max
M И z max
MИ


I y : z max 
Iy
(229)
44
Отношение момента инерции относительно нейтральной
линии (оси у) к расстоянию от этой линии до наиболее
удаленных точек сечения называют осевым или
экваториальным моментом сопротивления и обозначают Wу
т. e.
Iy
 Wy
(230)
z max
Тогда
MИ
(231)
 max 
Wy
Таким образом, наибольшие нормальные напряжения σmax
возникающие в каком-либо поперечном сечении балки,
равны частному от деления изгибающего момента в этом
сечении на осевой момент сопротивления
45
Обычно в выражения (228), (231) подставляют абсолютные
величины Ми и z, а знак нормальных напряжений
определяют следующим правилом: если рассматриваемая
точка находится в растянутой зоне сечения, то перед
выражениями (228), (231) следует ставить плюс, если в
сжатой — то минус. Положение растянутых и сжатых зон
определяется знаком изгибающего момента Mи. Так, при
положительном значении Mи волокна ниже нейтрального
слоя растягиваются, а выше— сжимаются, при
отрицательном Ми, наоборот, волокна ниже нейтрального
слоя сжимаются, а выше—растягиваются
46
Определение касательных напряжений
В общем случае при изгибе в поперечных сечениях балки
возникают изгибающий момент Ми и поперечная сила Q.
Поперечная сила Q является равнодействующей внутренних
усилий, лежащих в плоскости сечения, следовательно, в
поперечных сечениях возникают не только нормальные, но и
касательные напряжения τ. Исследования показывают, что
при наличии поперечной силы закон распределения
нормальных напряжений по сечению изменяется
незначительно, а поэтому их можно определять по формуле,
полученной для чистого изгиба.
47
При определении касательных напряжений в балке
прямоугольного поперечного сечения принимают, что они
направлены параллельно поперечной силе Q и что их
величины, как и величины нормальных напряжений, не
зависят от положения точки по ширине сечения, т. е. на
одном и том же расстоянии z от нейтральной линии
возникают равные между собой касательные .напряжения
(рис. 69, а). Эти допущения были сделаны в 1865г. Д. И.
Журавским и оказались достаточно правильными для
балок, у которых ширина прямоугольного сечения меньше
двух высот.
48
Вырежем из балки двумя смежными поперечными сечениями и
двумя смежными плоскостями, параллельными нейтральному
слою, элемент со сторонами dх и dz (рис. 69, а, б). Согласно
принятому допущению по его вертикальным граням, как
граням, совпадающим с поперечными сечениями, будут
действовать равномерно распределенные по всей ширине b
касательные напряжения τ. В соответствии с законом парности
по горизонтальным граням, совпадающим с продольными
сечениями, параллельными нейтральному слою, будут
действовать касательные напряжения, численно равные τ, но
противоположно направленные. Следовательно, касательные
напряжения в поперечных сечениях сопровождаются
касательными напряжениями в продольных сечениях,
параллельных нейтральному слою. Они, как и касательные
напряжения в поперечных сечениях, не зависят от положения
точек по ширине сечения.
49
рис. 69
50
Для определения касательных напряжений рассмотрим
однопролетную балку прямоугольного поперечного сечения,
высота которого h больше удвоенной ширины b (h>2b). Балка
нагружена сосредоточенной силой Р так, как это показано на рис.
70, а.
На некотором расстоянии х от левого конца балки двумя
бесконечно близкими поперечными сечениями т—т и n—п
мысленно выделим элемент длиной dх (см. рис. 70, а, б). Как
видно из эпюр Q и Ми, по сечению т—т этого элемента
действует изгибающий момент Ми(х), а по п—п, находящемуся на
расстоянии dх от т—т, изгибающий момент Ми (х)=dМи(х);
поперечные силы Q(х) в обоих сечениях одинаковы. Теперь
разрежем рассматриваемый элемент по сечению l—l,
проходящему параллельно нейтральному слою на некотором
расстоянии z от него, на две части и отбросим верхнюю.
Действие отброшенной части на оставшуюся нижнюю заменим
касательными напряжениями τ' (см. рис. 70, в). В соответствии с
законом парности эти касательные напряжения должны быть
численно равны касательным напряжениям τ в точках
поперечных сечений т—т и п—п на том же расстоянии z от
нейтрального слоя, т. е. τ'=τ.
51
На рис. 70, в в аксонометрической проекции и более крупном
масштабе изображена оставшаяся нижняя часть элемента
балки. Выясним, какие усилия, проектирующиеся на ось х,
действуют по граням этой части элемента. Как видно из рис.
70, в, касательные напряжения τ' по горизонтальной грани l—l
создают усилие
(232)
T   ' bdx  bdx
В поперечном сечении т—т действует изгибающий момент
Ми(х), а в сечении п—п—изгибающий момент Ми(х)+ dМи(х).
Следовательно, по граням т—m и п—n, являющимся частями
сечений т—т и п—п, действуют нормальные напряжения
M И x z
m 
Iy
(233)
n

M И x   dM И x z

(234)
Iy
52
Эпюры напряжений σm и σn показаны на рис. 70, в. Эти
нормальные напряжения создают нормальные усилия ∆Nm и
∆Nn действующие соответственно по граням т—l и п—l.
Если dNm = σmdF —элементарное нормальное усилие,
приходящееся на площадку dF грани т—l, взя той на
некотором расстоянии z1 от нейтральной линии, то
N m   dN m    m dF
F1
F1
53
рис. 70 а,б
54
рис. 70 в,г
55
Здесь F1=b(zтax—z)—площадь грани т—l, т. е. площадь
части сечения т—т от уровня z до нижнего края балки
(см. рис. 70, б).
С учетом (233) нормальная сила
M И x 
M И x 
N m  
z1 dF 
z1 dF

Iy
I y F1
F1
56
В этом выражении величина —  z1dF  S y z  статический
F
момент относительно нейтральной
линии (оси у) части
площади сечения т—т, лежащей ниже уровня z, на котором
действуют касательные напряжения τ. Следовательно,
M И x 
N m 
S y z 
Iy
(235)
Аналогично нормальное усилие, действующее по грани n—l,
M И x   dM И x 
(236)
N n 
S y z 
Iy
На рис. 70, г показан рассматриваемый элемент с
действующими по его граням усилиями ∆T, ∆Nm, ∆Nn. Так
как элемент в составе балки находился в равновесии, то для
него справедливо уравнение статики
 X  0;
N n  T  N m  0
57
Принимая во внимание (235) и (236), получим
M И x   dM И x 
M И x 
S y z   bdx 
S y ( z)  0
Iy
Iy
откуда, после приведения подобных членов и сокращений,
находим
dM И  x  S y  z 


(237)
dx
I yb
Учитывая, что
dM И x 
 Q x 
dx
(218)
формула для определения касательных напряжений в точках
поперечных сечений т—т и п—п на расстоянии z от
нейтральных линий примет вид
Q x S y  z 

(238)
I yb
58
Эта формула впервые была получена Д. И. Журавским и
носит его имя. Так как сечения т—т и п—п и расстояние z
от нейтрального слоя взяты произвольно, то формула
справедлива для определения касательных напряжений в
любом поперечном сечении на любом расстоянии z от
нейтрального слоя.
Несмотря на ограничение, сделанное при выводе формулы
Журавского (рассмотрено узкое прямоугольное сечение с h
: b>2), на практике эту формулу можно применять для
определения касательных напряжений в любых точках
любых форм сечений. Исключением из этого положения
являются сечения в виде узких прямоугольников,
расположенных параллельно нейтральной линии, например,
полок двутавра, швеллера и т. д.
59
В случае произвольной формы сечения (рис. 71) величины,
входящие в формулу (238), имеют следующие значения:
Q(х)—поперечная сила в сечении, где определяют τ; Iу —
момент инерции этого сечения относительно нейтральной
линии; b=b(z)—ширина сечения на уровне z, где вычисляют τ;
Sу(z)—статический момент относительно нейтральной линии
части сечения, которая лежит ниже или выше уровня z.
Заметим, что статический момент относительно нейтральной
линии части сечения, лежащей ниже уровня z, численно равен
статическому моменту части сечения, лежащей выше уровня
z. Это следует из того, что их сумма, равная статическому
моменту всего сечения относительно нейтральной линии
(линии , проходящей через центр тяжести, равна нулю, то эти
величины равны между собой по знаку.
60