max

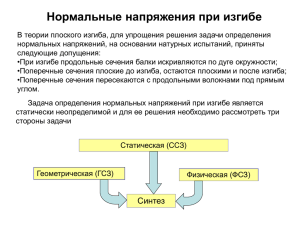
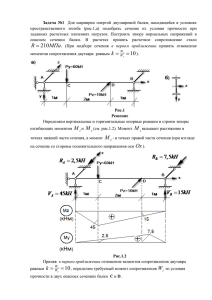
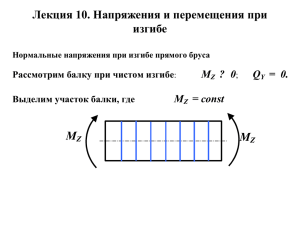
Лекция 10
§29 Условие прочности балки по нормальным напряжениям при
плоском изгибе балки
Для обеспечения прочности балки необходимо, чтобы наибольшие
растягивающие и наибольшие сжимающие напряжения при изгибе в опасном
сечении, то есть в сечении, где М имеет наибольшее значение, не
превосходили соответствующих допускаемых напряжений.
zmax
max
z
Пусть M = Mmax, Z = Zmax ;
Итак, условие прочности при изгибе:
или
(29.1)
§30 Определение касательных напряжений в балках при изгибе.
Условие прочности балки по касательным напряжениям
В общем случае изгиба (при поперечном изгибе) в поперечных
сечениях балки возникают изгибающие моменты и поперечные силы.
Наличие изгибающего момента связано с возникновением в поперечных
сечениях балки нормальных напряжений, для определения которых можно
пользоваться формулой (28.6).
Наличие поперечной силы связано с возникновением касательных
напряжений в поперечных сечениях балки, а по закону парности касательных
напряжений – и в ее продольных сечениях.
Для определения касательных напряжений рассмотрим в начале балку
прямоугольного сечения. Высота прямоугольного сечения h больше ширины
сечения b.
Для таких балок при вычислении касательных напряжений Д. И.
Журавским была принята следующие гипотезы:
1)
касательные напряжения в поперечных сечениях действуют
параллельно поперечной силе Q;
2)
касательные напряжения постоянны по ширине балки.
M
I
II

M+dM
III
y
0
h
z
III
x
x
dx
l
z
b
z
Выделим из балки элемент длиной dx и шириной, равной ширине b
балки сечениями I, II и III.
' I
II ''
N1
N2
z
T
I
 II
dx
x
Пусть в сечении I-I действует изгибающий момент М, а в сечении
II
M+dM.
Q = const.
Приложим к этому параллепипеду действующие на него нормальные и
касательные напряжения. Пусть
N1 – равнодействующая нормальных напряжений σ';
N2 – равнодействующая нормальных напряжений σ'';
Т – равнодействующая касательных напряжений τ.
T = τ · bdx.
Составим уравнения статического равновесия:
ΣХ= N2 – N1 – T = 0;
статический момент отсеченной площади поперечного
сечения ω относительно нейтральной оси y;
ω – часть площади поперечного сечения, заключенная между краем
сечения и уровнем исследуемых точек.
,
согласно диф. зависимости
– формула Журавского
(30.1)
Поясним значения величин, входящих в формулу (30.1):
b – ширина сечения на уровне исследуемых точек;
b

z
z1
, где z1 – координата у.т. площади ω.
y
z
Формула Журавского дает точный результат для балок прямоугольного
поперечного сечения и для балок, элементы, которых состоят из
прямоугольников и параллельны силе Q.
1)
h » b;
прямоугольное сечение:
h/2
max
h/2
z
y
b/2
b/2
z
Тогда
2)
поперечное сечение в форме двутавра:


t
F1
h
z
z2
z1
F2
d
max
b
b » d, поэтому
»
.
Следует подчеркнуть, что по формулам Журавского определяются
касательные напряжения, параллельные поперечной силе, то есть в данном
случае вертикальные.
Анализ точных решений теории упругости показывает, что в
большинстве
случаев
горизонтальные
составляющие
касательных
напряжений невелики.
Максимальное касательное напряжение имеет
место в точках
нейтральной оси и определяется по формуле Журавского, при этом следует
брать статический момент заштрихованной площади (полусечения). В
таблицах сортамента приведены значения статического момента площади
полусечения для двутавров и швеллеров.
Условие прочности по касательным напряжениям записывается в виде: