поляризованный свет
реклама
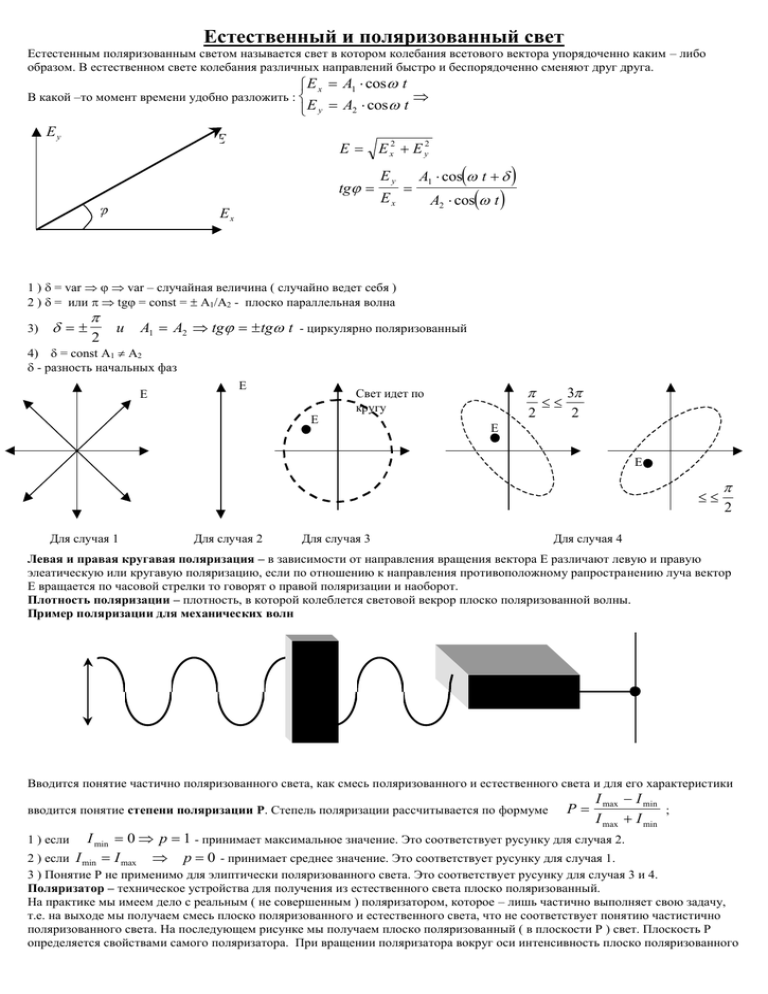
Естественный и поляризованный свет Естестенным поляризованным светом называется свет в котором колебания всетового вектора упорядоченно каким – либо образом. В естественном свете колебания различных направлений быстро и беспорядоченно сменяют друг друга. E x A1 cos t E y A2 cos t В какой –то момент времени удобно разложить : Ey E E tg Ex E x2 E y2 Ey Ex A1 cos t A2 cos t 1 ) = var var – случайная величина ( случайно ведет себя ) 2 ) = или tg = const = A1/A2 - плоско параллельная волна 3) 2 и A1 A2 tg tg t - циркулярно поляризованный 4) = const A1 A2 - разность начальных фаз Е Е Е 3 2 2 Свет идет по кругу Е Е 0 Для случая 1 Для случая 2 Для случая 3 2 Для случая 4 Левая и правая кругавая поляризация – в зависимости от направления вращения вектора Е различают левую и правую элеатическую или кругавую поляризацию, если по отношению к направления противоположному рапространению луча вектор Е вращается по часовой стрелки то говорят о правой поляризации и наоборот. Плотность поляризации – плотность, в которой колеблется световой векрор плоско поляризованной волны. Пример поляризации для механических волн Вводится понятие частично поляризованного света, как смесь поляризованного и естественного света и для его характеристики вводится понятие степени поляризации Р. Степель поляризации рассчитывается по формуме P I max I min ; I max I min I min 0 p 1 - принимает максимальное значение. Это соответствует русунку для случая 2. 2 ) если I min I max p 0 - принимает среднее значение. Это соответствует русунку для случая 1. 1 ) если 3 ) Понятие Р не применимо для элиптически поляризованного света. Это соответствует русунку для случая 3 и 4. Поляризатор – техническое устройства для получения из естественного света плоско поляризованный. На практике мы имеем дело с реальным ( не совершенным ) поляризатором, которое – лишь частично выполняет свою задачу, т.е. на выходе мы получаем смесь плоско поляризованного и естественного света, что не соответствует понятию частистично поляризованного света. На последующем рисунке мы получаем плоско поляризованный ( в плоскости Р ) свет. Плоскость Р определяется свойствами самого поляризатора. При вращении поляризатора вокруг оси интенсивность плоско поляризованного света не изменится, а будет меняться плоскость поляризации плоско поляризванного света ( направление колебания световой волны). Естественный свет Е I0 Iп P - Направление возможного поворота плоско поляризованного света I0 Р – плоскость поляризации; - интенсивность 1 I п I 0 = const 2 Поляризатор Во многоих оптических приборах применяется схема в которой находится два поляризатора последовательно помещенных друг за другом, при этом первый поляризатор выполняет ту самую функцию которая была описана ранее, а второй – анализирует это излучеие и позволяет определить степень поляризации. Второй поляризатор по своей функции называется анализатором. Если мы направим световую волну в противоположном направлении, то ничего не изменится, т.к. эти два устройства ничем не отличаются. 1 0 I0 2 Iп IA 1 I 2 0 поляризатор анализатор Iп 1 I 2 0 IA 0 Iп 1 I 2 0 IA 2 I0 3 0 1 I 2 0 2 I0 1 I cos 2 п Случай 2 – скрещенные поляризаторы. Наиболее используемый случай в технике. Все случай ( 1-3 ) представленны без учета : отражения от поверхностей, рассеивания оптических материалов, собственного поглащения ( считаел оптически прозрачные среды ) – идеальный поляризатор. Если мы имеем коэффициент отражения, то прошедший свет рассчитывается по формуле : I 1 1 R I 0 Коэффициентов ( 1-R ) будет столько через сколько плоскостей проходит луч. Закон Малюса : I A 1 I cos2 2 0 Виды поляризаторов : ( смотреть самостоятельно ); Наиболее известный вид : призма Николя; ( Два скрещенных Николя = два скрещенных поляризатора ); Поляризация при отражении и преломлении 2 D C 1 2 A B n1 1 2 n2 1 1 n1 n2 E1 E 2 ; D1n D2 n B1 B2 ; B1n B2 n d E l dl dl S B dS . E1 l 0 E1 E 2 K K1x K2 x 0x K1x K1 sin 1 K 2 x K2 sin 2 c n1 sin 1 c n2 sin 2 sin 1 n1 sin 2 n2 k2 E 2 E 2|| n2 n1 k1 E1 k1 E E1|| || 0 E 0 E 0 E1 E 2 n1 cos1 E 0 E1 n1 cos1 E 2 n1 E 0|| E1|| n2 E 2|| cos1 E 0|| E1|| cos1 E 2|| Две независимые линейные поляризации. sin1 2 E1 ; E0 sin1 2 E1|| tg1 2 E 0|| tg1 2 E1 E1|| n1 n2 E 2 E 2|| n1 n2 п ри 1 2 0 R R|| 1 1 R R 1 | | составляющая составляющая n1 R|| б р 2 n1 n2 б р 2 n2 2 n1 n2 2 При падении излучения под углом Брюстера получаем – коэффициент отражения для параллельной составляющей будет = 0. Тангенс угол Брюстера равен относительному показателю преломления n21 этих двух оптических сред. Доказать самостоятельно, что угол между преломленным и отраженным равен 90.Угол Брюстера для стекла 5657.









