Открытый урок в 9 классеx

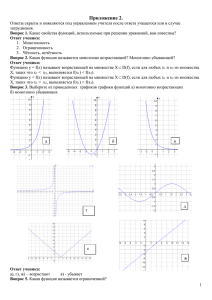
Свойства функций
Открытый урок в 9А классе (07.12.2010г)
Цели: изучить свойства функции; рассмотреть алгоритм прочтения свойств
функций; выяснить какими свойствами обладают некоторые ранее изученные
функции; развивать логическое мышление учащихся.
Ход урока
I.
Организационный момент
Сообщить тему урока, сформулировать цели урока.
II.
Актуализация знаний учащихся
Решение задач с целью подготовки к восприятию нового материала: задания на
готовых чертежах (фронтальная работа с использованием кодоскопа).
Вопросы:
1. Определите являются ли графиком какой-либо функции, линии изображенные на
рисунках.
2. Назовите область определения и область значений функций.
3. Что значит «Функция непрерывна на промежутке х»? Какие из представленных
функций непрерывны и на каком участке?
III. Изучение нового материала
1. Рассмотреть свойства возрастания (убывания) функции или свойство
монотонности.
В 7- 8 классах мы уже рассматривали некоторые свойства функций, сегодня нам
предстоит пополнить наши знания новыми сведениями. Во всех определениях будет
присутствовать числовое множество Х, являющееся частью области определения
функции: X⊂D(f).
а) Функция y=f(x) наз. возрастающей на множестве X⊂D(f), если для любых двух
точек х1 и х2 множества Х, таких, что х1<х2, выполняется неравенство f(x1)<f(x2).
На практике удобнее: функция возрастает, если большему значению аргумента
соответствует большее значение функции «поднимаемся в гору».
Запись в тетради: f ↑: если х1<х2, то f(x1)<f(x2).
б) Функция y=f(x) наз. убывающей на множестве X⊂D(f), если для любых двух
точек х1 и х2 множества Х, таких, что х1<х2, выполняется неравенство f(x1)> f(x2).
На практике удобнее: функция убывает, если большему значению аргумента
соответствует меньшее значение функции «спускаемся с горы».
Запись в тетради: f ↓: если х1<х2, то f(x1)>f(x2).
«Возрастающая функция», «убывающая функция» объединяют общим названием
монотонная функция.
Закрепить новые сведения: 1) по готовым чертежам устно определить
возрастание и убывание;
2) письменно в тетрадях №10.1, 10.2,10.4, 10.5 – «а, б» (доказательство
проводится на основании свойств числовых неравенств).
2. Рассмотреть свойство ограниченности функции.
а) Функцию y=f(x) наз. ограниченной снизу на множестве X⊂D(f), если существует
число m такое, что для любого значения x ∊ X выполняется неравенство f(x) > m.
График выше прямой y = m.
б) Функция y=f(x) наз. ограниченной сверху на множестве X⊂D(f), если существует
число M такое, что для любого значения x ∊ X выполняется неравенство f(x) < М.
График ниже прямой y = М.
Если функция ограничена и сверху, и снизу, то ее называют ограниченной (приведите
свои примеры).
Закрепить новые сведения: 1) по готовым чертежам найти ограниченные функции;
2) определить значения для m и M; 3) исследовать на ограниченность функцию
y  9  x 2 (работа с учебником стр.99); 4) письменно в тетрадях №10.7 - 10.8а,б.
III.
Закрепление изученного материала № 10.18, 10.20 – а
V. Итоги урока.
1. Перечислить все новые термины.
2. Домашнее задание: знать определения 1-4 стр. 97-98 кр. Учебника, выполнить
№ 10.1, 10.2, 10.4, 10.5, 10.7, 10.8 , 10.18, 10.20 – в,г,
3. Игровой момент:
Подберите из представленных графиков функций соответствующие для
предложенных пословиц.
- чем дальше в лес, тем больше дров;
- дальше от кумы – меньше греха;
- каши маслом не испортишь;
- выше меры конь не скачет;
- семь раз отмерь, один раз отрежь;
- бездонную бочку водой не наполнишь;
- где не было начала, не будет и конца;
- и сокол выше солнца не летает;
- тише едешь, дальше будешь.