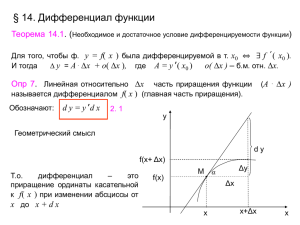
Тема 2.1.2. &quot

Инструкционно - технологическая карта практического
занятия №2.1.2.
Тема: « Основы дифференциального исчисления»
Наименование работы: «Нахождение производных высших порядков»
Цели занятия:
обучающая - закрепить умения и навыки, полученные в процессе
изучения темы «Производные функции»;
развивающая - развитие творческого мышления студентов;
воспитательная – продолжать формировать у студентов интерес к
математике с помощью решения прикладных задач. Показать студентам, что
одна и та же математическая модель может служить решением задач,
различных по своему содержанию.
Основные знания и умения:
Знать: определение второй производной; механический смысл второй
производной; понятие производной n –го порядка.
Уметь: находить производные высших порядков.
Формируемые компетенции:
Общие компетенции (ОК): ОК 2, ОК 4-5
 Организовать собственную деятельность, выбирать типовые методы и
способы вычисления производных высших порядков, оценивать их
эффективность и качество;
 Осуществлять поиск и использование информации для эффективного
выполнения вычислений производных высших порядков, профессионального и
личностного развития.
 Владеть информационной культурой, анализировать и оценивать
результаты своей работы.
Область применения общих компетенций: работа в качестве юриста
Обеспечение
занятия:
Мультимедийный проектор;
Раздаточный материал таблица «Основные формулы дифференцирования».
Профессиональный математический калькулятор «Machcad 13»;
Методические
рекомендации:
Вид занятия: применение знаний, умений и навыков
Мотивация
познавательной
деятельности
студентов:
Показать
практическую значимость понятия второй производной для физических и
технических дисциплин
План занятия:
Проверка домашнего задания:
Провести опрос в виде диктанта. Примерное содержание одного варианта:
1-3.Вписать пропущенные слова, дописать формулы.
1.Ускорение a(t) движения в данный момент времени t есть производная
скорости v(t) по времени, или … производная … по времени, т.е.
a(t)=
dv( t ) d ...
 2.
dt
dt
2.Уравнение касательной к графику функций f(x) имеет вид
у -…= …(х-х0).
3.Формулы производных: а) ( u  v )  ...; б) (cu)  ...; в) (...)  
г) (...)  uv  ...; д) (...)  nx ... ; е) f ( x )  f ...u...
v
;
v2
Повторение опорных знаний студентов:
Повторить со студентами основные определения, формулы, положения темы.
Применение знаний при решении типовых примеров: решить примеры с
целью подготовки к самостоятельной работе.
Выполнить упражнения:
1.Найти производные функций: И.И.Валуцэ § 37 №№ 7.78-7.84
1
6
2.Материальная точка движется по закону s(t)= t 3  3t 2  3t  1.
Найти а) момент времени t0, когда ускорение точки равно 0; б) скорость, с
которой движется точка в этот момент времени.
3.Тело массой 2кг движется прямолинейно по закону s(t )  5t 2  18t  1.
Найти силу, действующую на точку в момент времени t0=2c.
Подведение итогов занятия.
Домашнее задание: И.И.Валуцэ, Г.Д.Дилдигул гл.7 §37