(285.6 КБ)

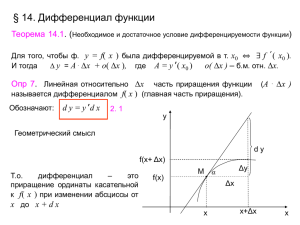
Производные и дифференциалы высших
порядков.
• Производные высших порядков. Свойства
• Кривизна плоской кривой
• Дифференциалы высших порядков.
Производные высших порядков
Если функция 𝑓(𝑥) имеет производную 𝑓 ′ 𝑥 в каждой точке
своей области определения, то ее производная 𝑓 ′ 𝑥 есть функция
от x . Производная второго порядка функции (или второй
𝑓′ 𝑥+∆𝑥 −𝑓′ (𝑥)
производной) есть 𝑓"(𝑥) = lim
.
∆𝑥→0
∆𝑥
Производная n-го порядка – производная от производной
(n-1)-го порядка, т.е.
𝑓 (𝑛)
=
′
(𝑛−1)
𝑓
=
∆𝑓(𝑛−1)
lim
.
∆𝑥→0 ∆𝑥
1. 𝑢 + 𝑣 (𝑛) = 𝑢(𝑛) + 𝑣 (𝑛) ,
2. 𝐶𝑢 (𝑛) = 𝐶 𝑢(𝑛) ,
3. Формула Лейбница* 𝑢𝑣 (𝑛) = 𝑛𝑘=0 𝐶𝑛𝑘 𝑢(𝑘) 𝑣 (𝑛−𝑘) .
_______________
Свойства:
*Го́тфрид Ви́льгельм Ле́йбниц (1646-1716) - немецкий философ, логик, математик, механик,
физик, юрист, историк, дипломат, изобретатель и языковед.
Кривизна плоской кривой
Кривизна кривой - предел отношения
угла поворота касательной ∆𝜑 к длине
пройденной дуги Δs, при стремлении
∆𝜑
последней к нулю: 𝐾 = lim .
∆𝑠→0 ∆𝑠
𝐾=
Так как 𝜑 𝑥 = 𝑎𝑟𝑐𝑡𝑔 𝑦 ′ 𝑥 , то 𝐾 =
В параметрическом виде: 𝐾 =
𝑑𝜑
𝑑𝑠
𝑦"
1+(𝑦′)2 3
|𝑥 ′ 𝑡 𝑦 " 𝑡 −𝑦 ′ 𝑡 𝑥"(𝑡)|
((𝑥′(𝑡))2 +(𝑦 ′ (𝑡))2 )3/2
Величина, обратная кривизне, называется радиусом кривизны: 𝑅 =
1
𝐾
Дифференциалы высших порядков
Дифференциалом n -го порядка функции называется
дифференциал от дифференциала (n-1)-го порядка этой
функции, то есть 𝑑𝑛 𝑓 = 𝑑 𝑑 𝑛−1 𝑓 .
𝑑2 𝑓 = 𝑑 𝑓′(𝑥)∆𝑥 = 𝑓"(𝑥)∆𝑥 2
𝑑2 𝑓 = 𝑓"(𝑥)𝑑𝑥 2
Свойства.
𝑓
𝑛
1. 𝑑 𝑛 𝑢 + 𝑣 = 𝑑𝑛 𝑢 + 𝑑𝑛 𝑣,
2. 𝑑 𝑛 𝐶𝑢 = 𝐶𝑑𝑛 𝑢,
3. 𝑑𝑛 𝑢𝑣 = 𝑛𝑘=0 𝐶𝑛𝑘 𝑑𝑘 𝑢 ∙ 𝑑𝑛−𝑘 𝑣
𝑑𝑛 𝑓
𝑥 = 𝑛
𝑑𝑥