d′ B′′ B′ f′ l d f B f B0 O′ M′ M O C d f лучу. Из

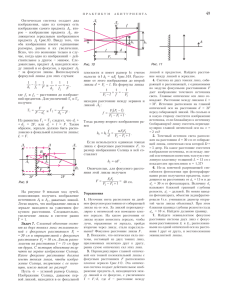
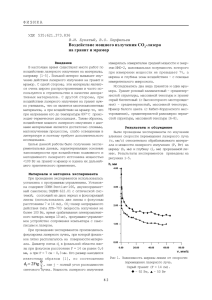
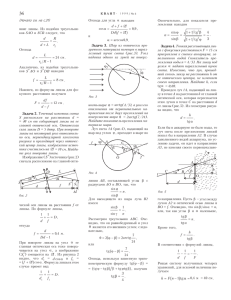
30
ÊÂÀÍT 2002/¹6
ëó÷ó. Èç òðåóãîëüíèêà BCD íàéäåì äëèíó ñòîðîíû ÂÑ:
a
BC =
cos β .
Èç òðåóãîëüíèêà ÂÑÅ ïî òåîðåìå ñèíóñîâ ìîæíî çàïèñàòü
BE sin ( α − β )
=
,
sin α
BC
îòêóäà ïîëó÷èì
u=v
sin ( α − β )
BE = a
cos β sin α .
Äëÿ ïàðàêñèàëüíûõ ëó÷åé, ò.å. äëÿ ëó÷åé, èäóùèõ ïîä
ìàëûìè óãëàìè ê ãëàâíîé îïòè÷åñêîé îñè ëèíçû, ìîæíî
ñ÷èòàòü, ÷òî sin ( α − β ) = α − β , sin α = α , à cos β = 1 .  ýòîì
ïðèáëèæåíèè
1

BE = a  1 −  .
n

Ðàññòîÿíèå ÂÅ ðàâíî ñìåùåíèþ èñòî÷íèêà ïî íàïðàâëåíèþ ê ëèíçå. Äî ïîìåùåíèÿ ïëàñòèíû èñòî÷íèê è åãî
èçîáðàæåíèå íàõîäèëèñü íà äâîéíîì ôîêóñíîì ðàññòîÿíèè
îò ëèíçû. Ïîñëå óñòàíîâëåíèÿ ïëàñòèíû èñòî÷íèê ïðèáëèçèëñÿ ê ëèíçå íà ðàññòîÿíèå AA′ = BE , à èçîáðàæåíèå
îòîäâèíóëîñü îò ëèíçû íà ∆ . Ïî ôîðìóëå ëèíçû ìîæíî
çàïèñàòü
1
1
1
+
= ,
d − AA′ d + ∆ F
èëè
1  F (d + ∆ )

d − a 1 −  =
.
n

 d+∆−F
Ðàçðåøàÿ ýòî ðàâåíñòâî îòíîñèòåëüíî n, ïîëó÷èì
 ( a − d )( d + ∆ − F ) + F ( d + ∆ ) 
n=

a (d + ∆ − F )


ëèòåëå ïðàâîé ÷àñòè ôîðìóëû ó÷èòûâàåò äâîéíîé ïðîõîä
ëó÷åé ÷åðåç ëèíçó.
Èç ïîäîáèÿ òðåóãîëüíèêîâ OO′M è M ′CO′ ñëåäóåò, ÷òî
d f = OM M ′C . Î÷åâèäíî, ÷òî OM M ′C = v u , ãäå u –
ñêîðîñòü èçîáðàæåíèÿ ìóõè. Ñëåäîâàòåëüíî,
−1
= 31 ≈ 1,48 .
21
Çàäà÷à 4.  êîìíàòå íà ñòîëå ëåæèò ïëîñêîå çåðêàëî, íà
êîòîðîì íàõîäèòñÿ òîíêàÿ ïëîñêîâûïóêëàÿ ëèíçà ñ ôîêóñíûì ðàññòîÿíèåì
O
B F = 40 ñì (ðèñ.5). Ïî
A
ïîòîëêó ÀÂ ïîëçåò
v
ìóõà ñî ñêîðîñòüþ
v = 2 ñì/c. Ðàññòîÿd
íèå îò ïîòîëêà äî
çåðêàëà d = 220 ñì.
Íà êàêîì ðàññòîÿíèè îò çåðêàëà íàO′
õîäèòñÿ èçîáðàæåÐèñ. 5
íèå ìóõè â äàííîé
îïòè÷åñêîé ñèñòåìå? ×åìó ðàâíà ñêîðîñòü èçîáðàæåíèÿ
ìóõè â òîò ìîìåíò, êîãäà îíà ïåðåñåêàåò ãëàâíóþ îïòè÷åñêóþ îñü ëèíçû OO′ ?
Ïóñòü ìóõà â íåêîòîðûé ìîìåíò íàõîäèòñÿ íà íåáîëüøîì
ðàññòîÿíèè ÎÌ îò ãëàâíîé îïòè÷åñêîé îñè ëèíçû (ðèñ.6).
Ïî ôîðìóëå ëèíçû ìû ìîæåì íàéòè, íà êàêîì ðàññòîÿíèè îò
ëèíçû íàõîäèòñÿ èçîáO
ðàæåíèå ìóõè M′:
M
1 1 2
+ = ,è
d f
F
d
M′ C
dF
= 22 ñì .
f =
2d − F
f
Çäåñü f – ðàññòîÿíèå îò
O′
èçîáðàæåíèÿ ìóõè äî
ëèíçû, à äâîéêà â ÷èñÐèñ. 6
f
= 0,2 ñì ñ .
d
Çàäà÷à 5. Ñ ïîìîùüþ ðàññåèâàþùåé ëèíçû ïîëó÷åíî
èçîáðàæåíèå ñïè÷êè, ðàñïîëîæåííîé ïåðïåíäèêóëÿðíî ãëàâíîé îïòè÷åñêîé îñè ëèíçû, ñ óâåëè÷åíèåì Γ1 = 1 2 . Ïî
äðóãóþ ñòîðîíó ëèíçû íà ðàññòîÿíèè l = 9 ñì îò íåå
ïåðïåíäèêóëÿðíî ãëàâíîé îïòè÷åñêîé îñè ëèíçû óñòàíîâèëè ïëîñêîå çåðêàëî. Èçîáðàæåíèå ñïè÷êè â ñèñòåìå ëèíçà –
çåðêàëî ïîëó÷èëîñü ñ óâåëè÷åíèåì Γ = 1 4 . Îïðåäåëèòå
ôîêóñíîå ðàññòîÿíèå ëèíçû.
Ðàññìîòðèì ñíà÷àëà ïåðâûé ñëó÷àé, êîãäà çåðêàëà íåò, à
ñ ïîìîùüþ ðàññåèâàþùåé ëèíçû ïîëó÷åíî èçîáðàæåíèå
ñïè÷êè ñ óâåëè÷åíèåì Γ1 . Îáîçíà÷èì ðàññòîÿíèå îò ñïè÷êè
äî ëèíçû ÷åðåç d, à îò èçîáðàæåíèÿ ñïè÷êè äî ëèíçû ÷åðåç
f. Ïî ôîðìóëå ëèíçû ìîæíî çàïèñàòü
1 1
1
− =− ,
d f
F
ãäå F – ôîêóñíîå ðàññòîÿíèå ëèíçû. Óìíîæèâ êàæäûé ÷ëåí
ýòîãî ðàâåíñòâà íà f, ïîëó÷èì
f
f
−1 = − .
d
F
Ñ ó÷åòîì òîãî, ÷òî f d = Γ1 , ìû ïîëó÷àåì îäíîçíà÷íóþ
ñâÿçü ìåæäó ðàññòîÿíèåì îò èçîáðàæåíèÿ äî ëèíçû è óâåëè÷åíèåì:
f = F (1 − Γ1 ) .
Ìíèìîå èçîáðàæåíèå  òî÷êè ñïè÷êè B0 â ëèíçå (ðèñ.7)
áóäåò ÿâëÿòüñÿ ïðåäìåòîì äëÿ ïëîñêîãî çåðêàëà. Ðàññòîÿíèå
îò ýòîãî ïðåäìåòà äî
çåðêàëà ðàâíî f + l.
Èçîáðàæåíèå B′ ýòîãî ïðåäìåòà â çåðêàB
B′′
B′
ëå íàõîäèòñÿ òàêæå B
íà ðàññòîÿíèè f + l îò
f
çåðêàëà. Ðàññòîÿíèå
îò èçîáðàæåíèÿ B′
l
äî ëèíçû ðàâíî d′ =
f′
d
= f + 2l. Îáîçíà÷èì
d′
ðàññòîÿíèå îò èçîáðàæåíèÿ B′′ â ëèíçå
Ðèñ. 7
÷åðåç f ′ è ñíîâà âîñïîëüçóåìñÿ ôîðìóëîé ëèíçû:
1
1
1
−
=− .
f + 2l f ′
F
f′
. Ñ äðóãîé
Óâåëè÷åíèå â ýòîì ñëó÷àå ðàâíî Γ 2 =
f + 2l
ñòîðîíû, Γ 2 = Γ Γ1 . Óìíîæèì âñå ÷ëåíû â ôîðìóëå ëèíçû
íà f + 2l, ïîäñòàâèì ðàíåå íàéäåííîå âûðàæåíèå äëÿ f è
ïîëó÷èì
2l
= 36 ñì .
F=
Γ1 + Γ1 Γ − 2
Çàäà÷à 6. Èç ñòåêëÿííîé ïëàñòèíêè ñ ïîêàçàòåëåì
ïðåëîìëåíèÿ n = 1,5 âûðåçàëè òîëñòóþ ëèíçó â ôîðìå
ïîëóøàðà ðàäèóñîì R = 10 ñì. ×åðåç òàêóþ ëèíçó ðàññìàòðèâàåòñÿ òî÷å÷íûé èñòî÷íèê ñâåòà S, ðàñïîëîæåííûé íà
ðàññòîÿíèè d = R/2 îò ïëîñêîé ïîâåðõíîñòè ïîëóøàðà
(ðèñ.8). Íà êàêîì ðàññòîÿíèè îò ýòîé ïîâåðõíîñòè íàáëþ-