Täiendusõppe õppekava RXC0016 - Matemaatika (lai kursus) Курс

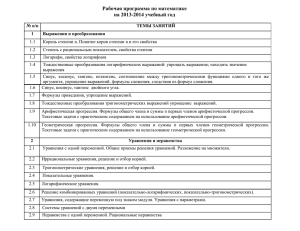
Täiendusõppe õppekava
RXC0016 - Matemaatika (lai kursus)
TTÜ Virumaa Kolledž
õppekava kood
RXC0016
nimetus e.k.
Matemaatika (lai kursus)
nimetus v.k.
Математика (широкий курс)
õppeviis
kontaktõpe, iseseisev õpe
koolituse liik
kursus
maht tundides
156 sh. kontaktõpe - 80, iseseisev õpe - 76, muu - 0
kursus on seotud
EAP-dega
jah
õppekava maht (EAP) 6
vene
õppetöö keeled
kontrollivorm
arvestus
hindamiskriteeriumid
v.k.
В процессе прохождения данного курса необходимо выполнить 11
контрольных домашних работ на оценку "зачтено" (60% работы
выполнено успешно). Посещаемость не менее 75%.
eesmärgid v.k.
Повторение основных тем гимназического курса математики для
подготовки к вступительному экзамену по математике в ТТУ; создание
базы для успешного усвоения математических дисциплин в ТТУ.
õpiväljundid v.k.
Успешно окончивший данный курс умеет решать типичные задачи
гимназического курса математики и знает используемые в них
понятия.
sisu v.k.
Курс состоит из трех модулей:
I УРАВНЕНИЯ И НЕРАВЕНСТВА. ВЕКТОРЫ. ПРОГРЕССИЯ.
Действительные числа и выражения: Процент числа. Деление числа
на части, пропорциональные данным. Формулы сокращенного
умножения. Действия с алгебраическими дробями. Степени и корни.
Уравнения и неравенства: Числовые множества. Квадратные и
биквадратные
уравнения.
Дробно-рациональные
уравнения.
Неравенства с одним неизвестным. Метод интервалов. Уравнения с
параметрами. Системы линейных уравнений и неравенств.
Числовая
последовательность.
Предел
числовой
последовательности.
Арифметическая
и
геометрическая
прогрессия: Общий член числовой последовательности. Свойства
предела числовой последовательности. Формула общего члена
арифметической прогрессии. Сумма n членов арифметической
прогрессии. Общий член геометрической прогрессии. Формула суммы
n членов геометрической прогрессии. Бесконечно убывающая
геометрическая прогрессия.
Вектор на плоскости. Уравнение линии: Координаты вектора. Длина
вектора. Координаты середины отрезка. Алгебраические операции над
векторами.
Скалярное
произведение
векторов.
Векторное
произведение векторов. Уравнение прямой с заданным угловым
коэффициентом и проходящей через данную точку. Уравнение прямой,
проходящей через две точки плоскости. Взаимное расположение
прямых на плоскости. Уравнение параболы и окружности.
II ФУНКЦИИ.
Функции и их графики: Основные элементарные функции и их
графики. Область определения функции. Основные характеристики
функции. Преобразование графиков.
Логарифмическая и показательная функция. Логарифмические,
показательные уравнения и неравенства: Логарифм числа. Свойства
логарифмов. Логарифмическая и показательная функции, их свойства
и графики. Логарифмические и показательные уравнения и
неравенства.
Тригонометрические уравнения и неравенства: Основные
тригонометрические
функции
и
их
графики.
Обратные
тригонометрические функции и их графики. Графическое и
аналитическое решение тригонометрических уравнений и неравенств.
Предел и производная функции: Предел функции. Производная
функции. Правила дифференцирования. Дифференцирование сложной
функции. Геометрическое и физическое приложение производной.
III ГЕОМЕТРИЯ. ТЕОРИЯ ВЕРОЯТНОСТИ.
ИНТЕГРАЛ.
Геометрия на плоскости и в пространстве: Плоские фигуры
(треугольник, параллелограмм, ромб, трапеция, окружность) и их
свойства. Призма и пирамида. Цилиндр, конус, сфера.
Теория вероятностей и описательная статистика: События.
Классификация событий. Классическая вероятность. Геометрическая
вероятность. Комбинаторика. Статистическая обработка данных.
Основные числовые характеристики (среднее, мода, медиана,
стандартное отклонение).
Интеграл: Неопределенный интеграл и его свойства. Определенный
интеграл.
Свойства
определенного
интеграла.
Формула
Ньютона-Лейбница. Интегрирование простейших функций. Площадь
криволинейной трапеции.