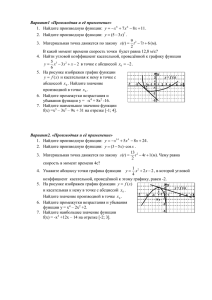
Вариант 1. 1. Найдите производную функции f(x) = . 2. Найдите
реклама

Вариант 1. 1. Найдите производную функции f(x) = х х х . 2. Найдите значение производной функции f(x) = 3х3 – 4х2 - 1 в точке х0 = - 1. 3. Найдите значение скорости тела, движущегося по закону s(t) = 2t3 – 2t2 + 2 в момент времени t0 = 2 сек. 4. Движение точки задано уравнением s(t) = 7t9 + 4t - 2 . В какой момент времени её скорость будет равна 4м/с ? 5. Найдите тангенс угла наклона касательной к оси Ох, проходящей через точку с абсциссой х0 = - 1 графика функции f(x) = х2 + 3,5х. 6. Напишите уравнение касательной к графику функции f(x) = х4 – 7х3 + 12х - 45 абсциссой х0 = 0. 7. Найдите производную функции 8. Найдите f(x) = е х в точке с . f '''(х), если f(x) = х4 + sinx . 9. Найдите точки экстремума функции f(x) = х - х2 + 6х – 1. 10 . Найдите наибольшее и наименьшее значение функции промежутке [1; 2]. f(x) = х3 + 3х2 – 45х – 2 на ____________________________________________________________________________ Вариант 2. 1. Найдите производную функции f(x) = (х2 – 2х)(х3 – 3). 2. Найдите значение производной функции f(x) = tg x в точке x0 = . 3. Найдите значение скорости тела, движущегося по закону s(t) = t4 + 1,5t2 - 15 в момент времени t0 = 1 сек. 4. Движение точки задано уравнением s(t) = 2t2 - 4t – 5,5 . В какой момент времени её скорость будет равна 8 м/с ? 5. Найдите тангенс угла наклона касательной к оси Ох, проходящей через точку с абсциссой х0 = - 1 графика функции f(x) = х3 – х2. 6. Напишите уравнение касательной к графику функции f(x) = абсциссой х0 = 2. 7. Найдите производную функции 8. Найдите f '''(х), если f(x) = х2 - 1 в точке с f(x) = (8х4 – 7)10 . cos x – 2x5. 9. Найдите промежутки монотонности функции f(x) = 2х3 – 3х2 – 36х + 40. 10 . Найдите наибольшее и наименьшее значение функции промежутке [-2; -0,5]. f(x) = - 2 х3– 3х2 + 4 на Вариант 3. х 1. Найдите производную функции f(x) = х . 2. Найдите значение производной функции f(x) = 2х4 – 4х2 - 1 точке в точке х0 = - 2. в 3 . Найдите значение скорости тела, движущегося по закону s(t) = 2,5t3 – 1,5t2 - 3 в момент времени t0 = 1 сек. 4. Движение точки задано уравнением s(t) = 5t2 - 16t + 4 . В какой момент времени её скорость будет равна 4 м/с ? 5. Найдите тангенс угла наклона касательной к оси Ох, проходящей через точку с абсциссой х0 = графика функции f(x) = 2 cos x. 6. Напишите уравнение касательной к графику функции абсциссой х0 = 0. 7. Найдите производную функции 8. Найдите f '''(х), если f(x) = f(x) = 2 – х –х3 в точке с . f(x) = ех – 2х6. 9. Найдите точки экстремума функции f(x) = х3 – 7х2 – 5х + 11 . 10 . Найдите наибольшее и наименьшее значение функции промежутке [-1;1]. f(x) = х5 – 4х2 на _______________________________________________________________________________ Вариант 4. 1. Найдите производную функции f(x) = (5 – х3)(7х – х2). 2. Найдите значение производной функции f(x) = arccos x в точке x0 = 1. 3. Найдите значение скорости тела, движущегося по закону s(t) = t3 + 2t2 + 5t в момент времени t0 = 1 сек. 4. Движение точки задано уравнением s(t) = х3 – 12х2 . В какие моменты времени её скорость будет равна 0 м/с? 5. Найдите тангенс угла наклона касательной к оси Ох, проходящей через точку с абсциссой х0 = - 1 графика функции f(x) = х3 – х2. 6. Напишите уравнение касательной к графику функции f(x) = 5х2 - 2 х0 = 6. 7. Найдите производную функции 8. Найдите в точке с абсциссой f(x) = sin ( ln x) f '''(х), если f(x) = 2 ех – х5. 9. Найдите промежутки монотонности функции f(x) = 60 +45х -3х2 – х3. 10 . Найдите наибольшее и наименьшее значение функции промежутке [-1;3]. f(x) = х3 – 9х2 + 24х - 1 на