Домашнее задание по алгебре
реклама

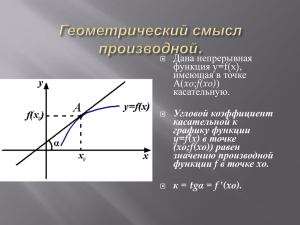
Домашнее задание по теме: «Геометрический и физический смысл производной» 2 1. Найдите тангенс угла наклона касательной, проведенной к графику функции 𝑦 = 6𝑥 − 𝑥 в его точке с 2. 3. 4. 5. абсциссой (-1). Найдите угловой коэффициент касательной к графику функции 𝑦 = 𝑠𝑖𝑛2𝑥 в его точке с абсциссой 0. Найдите площадь треугольника, который образует касательная к графику функции 𝑔(𝑥) = 𝑥 −1 в точке с абсциссой 1 с осями координат. Тело движется по прямой так, что расстояние от начальной точки изменяется по закону 𝑆(𝑡) = 5𝑡 + 0,2𝑡 3 − 6 (м), где t – время движения в секундах. Найдите скорость тела через 5 секунд после начала движения. Найдите угловой коэффициент касательной к графику функции 𝑔(𝑥) = (𝑥 − 1)2 (𝑥 + 1)2 − (𝑥 2 + 1)2 , проведенной в точке с абсциссой 1. 1−2𝑥 6. Найдите угловой коэффициент касательной к графику функции 𝑔(𝑥) = 4𝑥+1 , проведенной в точке с абсциссой -0,5. 7. Найдите тангенс угла наклона касательной, проведенной к графику функции 𝑦 = (𝑥 + 1)(𝑥 5 − 𝑥 4 + +𝑥 3 − 𝑥 2 + 𝑥 − 1) в его точке с абсциссой -1. 8. Найдите тангенс угла наклона касательной, проведенной к графику функции 𝑦 = 2𝑠𝑖𝑛𝑥 − 3𝑐𝑡𝑔𝑥 в его 𝜋 точке с абсциссой 3 . 9. Тело движется по прямой так, что расстояние 𝑆 (в метрах) от него до точки С этой прямой изменяется по закону 𝑆(𝑡) = 𝑡 3 − 𝑡 2 (t – время движения в секундах). Через сколько секунд после начала движения ускорение тела будет равно 40 м/с2? 10. Через точку М(−1; 0) к графику функции 𝑦 = √2𝑥 − 1 проведена касательная. Напишите её уравнение. В ответе укажите градусную меру угла наклона между касательной и положительным направлением оси Ох.