КПД термодинамических циклов
реклама

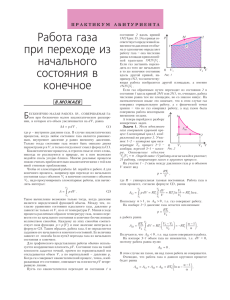
ÏÐÀÊÒÈÊÓÌ ÀÁÈÒÓÐÈÅÍÒÀ ÊÏÄ òåðìîäèíàìè÷åñêèõ öèêëîâ Â.ÄÐÎÇÄÎÂ Ó ÊÀÇÀÍÍÀß Â ÇÀÃËÀÂÈÈ ÑÒÀÒÜÈ ÒÅÌÀ ÔÀÊÒÈ×ÅÑÊÈ ÇÀ- âåðøàåò øêîëüíûé êóðñ òåðìîäèíàìèêè. Ïîýòîìó äëÿ ðåøåíèÿ çàäà÷ íà îïðåäåëåíèå ÊÏÄ öèêëîâ òðåáóåòñÿ çíàíèå ïî÷òè âñåãî ïðåäøåñòâóþùåãî ìàòåðèàëà.  ñèëó ýòîãî îáñòîÿòåëüñòâà, òàêèå çàäà÷è ÷àñòî èñïîëüçóþòñÿ äëÿ ïðîâåðêè çíàíèé ó÷àùèõñÿ íà ýêçàìåíàõ, â òîì ÷èñëå è â ôîðìå ÅÃÝ. Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ η òåðìîäèíàìè÷åñêîãî öèêëà îïðåäåëÿåòñÿ ïî ôîðìóëå A Q1 − Q2 Q η= = = 1− 2 , Q1 Q1 Q1 ãäå Q1 êîëè÷åñòâî òåïëîòû, ïîäâåäåííîå ê ðàáî÷åìó òåëó (ãàçó) çà öèêë îò íàãðåâàòåëÿ, Q2 êîëè÷åñòâî òåïëîòû, îòäàííîå ðàáî÷èì òåëîì çà öèêë õîëîäèëüíèêó, A = Q1 − Q2 ðàáîòà ãàçà çà öèêë. Îãðàíè÷èìñÿ ñëó÷àåì, êîãäà ðàáî÷èì òåëîì ÿâëÿåòñÿ èäåàëüíûé îäíîàòîìíûé ãàç. Ñîãëàñíî ïåðâîìó çàêîíó òåðìîäèíàìèêè, êîëè÷åñòâî òåïëîòû Q12 , ïîëó÷åííîå èäåàëüíûì ãàçîì ïðè ïåðåõîäå èç ñîñòîÿíèÿ 1 â ñîñòîÿíèå 2, ðàâíî ñóììå èçìåíåíèÿ âíóòðåííåé ýíåðãèè ãàçà è ñîâåðøåííîé èì ðàáîòû: Q12 = (U2 − U1 ) + A12 . Âíóòðåííÿÿ ýíåðãèÿ èäåàëüíîãî îäíîàòîìíîãî ãàçà ñ ó÷åòîì óðàâíåíèÿ ÊëàïåéðîíàÌåíäåëååâà ìîæåò áûòü çàïèñàíà â âèäå 3 3 U = νRT = pV , 2 2 ãäå ν êîëè÷åñòâî ìîëåé ãàçà, Ò òåìïåðàòóðà ãàçà, ð åãî äàâëåíèå, V îáúåì, R óíèâåðñàëüíàÿ ãàçîâàÿ ïîñòîÿííàÿ. Ðàáîòà ãàçà A12 ÷èñëåííî ðàâíà ïëîùàäè ïîä ãðàôèêîì çàâèñèìîñòè äàâëåíèÿ îò îáúåìà, âûðàæåííîé â ýíåðãåòè÷åñêèõ åäèíèöàõ (â ÑÈ â äæîóëÿõ). Òåïåðü ïåðåõîäèì ê ðàññìîòðåíèþ êîíêðåòíûõ çàäà÷. Çàäà÷à 1. Íàéäèòå ÊÏÄ öèêëà, èçîáðàæåííîãî íà ðèñóíêå 1. Ðåøåíèå. Ëåãêî âèäåòü, ÷òî ðàáîòà ãàçà çà öèêë ðàâíà 1 1 A = (2 p0 − p0 )(2V0 − V0 ) = p0V0 . 2 2 Îñòàëîñü íàéòè ïîäâåäåííîå ê ãàçó êîëè÷åñòâî òåïëîòû Q1 . Íà ó÷àñòêå 12 ðàáîòà ãàçà ðàâíà íóëþ, à äàâëåíèå ðàñòåò ïðè ïîñòîÿííîì îáúåìå, ò.å. òåìïåðàòóðà ãàçà ïîâûøàåòñÿ. Çíà÷èò, íà ýòîì ó÷àñòêå ãàç ïîëó÷àåò òåïëî. Íà ó÷àñòêå 23 ðàáîòà ãàçà A23 ïîëîæèòåëüíà, à îáúåì ðàñòåò ïðè ïîñòîÿííîì äàâëåíèè, ò.å. òåìïåðàòóðà ãàçà ðàñòåò. Ðèñ. 1 Ñëåäîâàòåëüíî, íà ýòîì ó÷àñòêå ãàç òîæå ïîëó÷àåò òåïëî. À âîò íà ó÷àñòêå 31 ðàáîòà ãàçà îòðèöàòåëüíà (èáî ãàç ñæèìàþò), ê òîìó æå îäíîâðåìåííî ïàäàþò è äàâëåíèå è îáúåì ãàçà, ÷òî ïðèâîäèò ê îõëàæäåíèþ ãàçà. Èíûìè ñëîâàìè, íà ó÷àñòêå 31 ãàç òåïëî íå ïîëó÷àåò. Èòàê, Q1 = Q12 + Q23 = = (U2 − U1 ) + A23 + (U3 − U2 ) = (U3 − U1 ) + A23 . Ó÷èòûâàÿ, ÷òî A23 = 2 p0 (2V0 − V0 ) = 2 p0V0 , ïîëó÷àåì 3 13 3 Q1 = ⋅ 2 p0 ⋅ 2V0 − p0V0 + 2 p0V0 = p0V0 . 2 2 2 Òåïåðü íàõîäèì ÊÏÄ öèêëà: η= (1 2) p0V0 = 1 ≈ 7,7% A = . Q1 (13 2) p0V0 13 Çàäà÷à 2. Íà ðèñóíêå 2 èçîáðàæåí öèêë äèçåëüíîãî äâèãàòåëÿ, ñîñòîÿùèé èç àäèàáàò 12 è 34, èçîáàðû 23 è èçîõîðû 41. Òåìïåðàòóðû ãàçà â òî÷êàõ 1, 2, 3, 4 ðàâíû T1 , T2 , T3 , T4 ñîîòâåòñòâåííî. Íàéäèòå ÊÏÄ öèêëà. Ðåøåíèå. Ðàáîòó ãàçà êàê «ýíåðãåòè÷åñêóþ ïëîùàäü» öèêëà çäåñü âû÷èñëèòü íåëåãêî öèêë êðèâîëèíåéíûé. Íî â ýòîì íåò íèêàêîé íóæäû. Âû÷èñëèì ÊÏÄ ÷åðåç ïîäâåäåííîå è îòâåäåí- Ðèñ. 2 íîå êîëè÷åñòâà òåïëîòû Q1 è Q2 . Åñòåñòâåííî, íà àäèàáàòàõ òåïëî íå ïîäâîäèòñÿ è íå îòâîäèòñÿ. Íà èçîáàðå 23 òåïëî ïîäâîäèòñÿ, èáî îáúåì ðàñòåò è, ñîîòâåòñòâåííî, ðàñòåò òåìïåðàòóðà. Íà èçîõîðå 4 1 òåïëî îòâîäèòñÿ, òàê êàê äàâëåíèå è òåìïåðàòóðà ïàäàþò. Òàêèì îáðàçîì, 3 Q1 = Q23 = (U3 − U2 ) + A23 = νR (T3 − T2 ) + p2 (V3 − V2 ) = 2 3 5 = νR (T3 − T2 ) + νR (T3 − T2 ) = νR (T3 − T2 ) . 2 2 Àíàëîãè÷íî, Q2 = U4 − U1 = Îêîí÷àòåëüíî ïîëó÷àåì η = 1− 3 νR (T4 − T1 ) . 2 3 (T4 − T1 ) Q2 = 1− . Q1 5 (T3 − T2 ) Çàäà÷à 3 (ÌÈÝÌ, 1990). Îïðåäåëèòå ÊÏÄ öèêëà, ñîñòîÿùåãî èç äâóõ àäèàáàò è äâóõ èçîõîð (ðèñ.3). Èçâåñòíî, ÷òî â ïðîöåññå àäèàáàòíîãî ðàñøèðåíèÿ óñòàíàâëèâàåòñÿ òåìïåðàòóðà T2 = 0,75T1 , à â ïðîöåññå àäèàáàòíîãî ñæàòèÿ T3 = 0,75T4 . Ðåøåíèå. Íà èçîõîðå 41 òåïëî ïîäâîäèòñÿ, íà Ðèñ. 3 ÏÐÀÊÒÈÊÓÌ èçîõîðå 23 òåïëî îòâîäèòñÿ, íà îáåèõ àäèàáàòàõ òåïëîîáìåíà íåò. Êðîìå òîãî, ðàáîòà íà èçîõîðàõ íå ñîâåðøàåòñÿ. Ïîýòîìó Q1 = U1 − U4 , Q2 = U2 − U3 . Çíà÷èò, U − U3 T − T3 Q2 = 1− 2 = 1− 2 . Q1 U1 − U4 T1 − T4 Ñ ó÷åòîì óñëîâèÿ çàäà÷è îêîí÷àòåëüíî ïîëó÷àåì η = 1− 0,75T1 − 0,75T4 η = 1− = 1 − 0,75 = 0,25 = 25% . T1 − T4 Çàäà÷à 4 (ÌÔÒÈ, 1989). ÊÏÄ òåïëîâîé ìàøèíû, ðàáîòàþùåé ïî öèêëó, ñîñòîÿùåìó èç èçîòåðìû 12, èçîõîðû 23 è àäèàáàòû 31 (ðèñ.4), ðàâåí η . Ðàçíîñòü ìàêñèìàëüíîé è ìèíèìàëüíîé òåìïåðàòóð ãàçà â öèêëå ñîñòàâëÿåò ∆T . Íàéäèòå ðàáîòó, ñîâåðøåííóþ ν ìîëÿìè ãàçà â èçîòåðìè÷åñêîì ïðîöåññå. Ðåøåíèå. Õîòÿ â äàííîé çàäà÷å ÊÏÄ èçâåñÐèñ. 4 òåí, âûðàçèì åãî, êàê è â ïðåäûäóùèõ çàäà÷àõ, ÷åðåç êîëè÷åñòâà òåïëîòû Q1 è Q2 è èñêîìóþ ðàáîòó A12 . Òàê êàê òî÷êè 1 è 2 ëåæàò íà îäíîé èçîòåðìå, òî T1 = T2 è, ñîîòâåòñòâåííî, U2 = U1 . ßñíî, ÷òî ∆T = T2 − T3 , âåäü òî÷êà 3 ëåæèò íèæå òî÷êè 2. Òîãäà Q1 = Q12 = A12 . Òåïëî íà èçîòåðìå äåéñòâèòåëüíî ïîäâîäèòñÿ, ïîñêîëüêó ðàáîòà ðàñøèðåíèÿ ãàçà A12 çàâåäîìî ïîëîæèòåëüíà. À íà èçîõîðå òåïëî îòâîäèòñÿ, ïðè÷åì 3 3 Q2 = Q23 = U2 − U3 = νR (T2 − T3 ) = νR∆T . 2 2 Ñëåäîâàòåëüíî, η = 1− (3 2 ) νR∆T Q2 = 1− , Q1 A12 îòêóäà íàõîäèì A12 1,5νR∆T = . 1− η Çàäà÷à 5 (ÌÔÒÈ, 2005).  öèêëå 1341 (ðèñ.5) ÊÏÄ ðàâåí η . ×åìó ðàâåí ÊÏÄ η′ öèêëà 12341? Ðåøåíèå. Òàê êàê äèàãîíàëü ïðÿìîóãîëüíèêà äåëèò åãî íà äâà ðàâíûõ òðåóãîëüíèêà, ðàáîòà, ñîÐèñ. 5 âåðøåííàÿ âî âòîðîì öèêëå 12341, âäâîå áîëüøå ðàáîòû À â ïåðâîì öèêëå 1341.  ïåðâîì öèêëå òåïëî, î÷åâèäíî, ïîäâîäèòñÿ òîëüêî íà ó÷àñòêå 13. Ïðè ýòîì Q1 = Q13 = A13 + (U3 − U1 ) , ãäå A13 = A + p1 (V4 − V1 ) . ÀÁÈÒÓÐÈÅÍÒÀ Çíà÷èò, A A = Q1 A + p1 (V4 − V1 ) + (U3 − U1 ) . η= Âî âòîðîì öèêëå òåïëî ïîäâîäèòñÿ òîëüêî íà ó÷àñòêàõ 12 è 23: Q1′ = Q12 + Q23 = (U2 − U1 ) + (U3 − U2 ) + A23 = (U3 − U1 ) + A23, ãäå A23 = 2 A + p1 (V4 − V1 ) . Ñëåäîâàòåëüíî, η′ = 2A 2A = . ′ Q1 2 A + p1 (V4 − V1 ) + (U3 − U1 ) Âûðàçèâ âåëè÷èíó p1 (V4 − V1 ) + (U3 + U1 ) èç óðàâíåíèÿ äëÿ η , íàõîäèì 2η η′ = . η+1 Çàäà÷à 6 (ÌÈÝÌ). Îïðåäåëèòå ÊÏÄ öèêëà (ðèñ.6), ñîâåðøàåìîãî ν = 3 ìîëü ãàçà è ñîñòîÿùåãî èç èçîõîðû, àäèàáàòû è èçîáàðû, åñëè èçâåñòíî, ÷òî ãàç ïîëó÷èë Q1 = 3000 Äæ òåïëà è â ðåçóëüòàòå àäèàáàòíîãî ðàñøèðåíèÿ òåìïåðàòóðà åãî ïîíèçèëàñü íà Ðèñ. 6 ∆T = 40 Ê. Ðåøåíèå. Î÷åâèäíî, ÷òî ãàç ïîëó÷àåò òåïëî íà èçîõîðå 12 è îòäàåò åãî íà èçîáàðå 31. Ïîýòîìó 3 Q1 = U2 − U1 = ( p2V2 − p1V1 ) , 2 Q2 = p1 (V3 − V1 ) + (U3 − U1 ) = = p3V3 − p1V1 + 3 3 5 p3V3 − p1V1 = ( p3V3 − p1V1 ) . 2 2 2 Çàïèøåì óðàâíåíèÿ ñîñòîÿíèÿ ãàçà â òî÷êàõ 2 è 3: p2V2 = νRT2 , p3V3 = νRT3 . Îòñþäà âûòåêàåò, ÷òî p2V2 − p3V3 = νR (T2 − T3 ) = νR∆T . Ïî îïðåäåëåíèþ òåðìîäèíàìè÷åñêîãî êîýôôèöèåíòà ïîëåçíîãî äåéñòâèÿ, Q η = 1− 2 . Q1 Ïðèõîäèì ê ñèñòåìå óðàâíåíèé Q2 η = 1 − Q , 1 3 Q1 = ( p2V2 − p1V1 ), 2 5 Q2 = ( p3V3 − p1V1 ), 2 p2V2 − p3V3 = νR∆T. Ïîñëåäîâàòåëüíî èñêëþ÷èâ èç ýòîé ñèñòåìû p3V3 , p2V2 − p1V1 è Q2 , ïðèõîäèì ê îòâåòó η= 5νR∆T 2 − = 0,16 = 16% . 2Q1 3 Çàäà÷à 7 (ÌÈÝÌ, 1991). Ãàç ñîâåðøàåò öèêë, èçîáðàæåííûé íà ðèñóíêå 7 â êîîðäèíàòàõ ð è U, ãäå ð äàâëåíèå, U âíóòðåííÿÿ ýíåðãèÿ ãàçà. Îïðåäåëèòå ÊÏÄ öèêëà. Ðåøåíèå. Ïðåæäå âñåãî ïðåäñòàâèì öèêë â êîîðäèíàòàõ ð, V. Ðèñ. 7 Çàïèøåì âíóòðåííèå ýíåðãèè ãàçà â âåðøèíàõ òðàïåöèè 1 è 3: 3 3 U0 = p0V1 , 4U0 = ⋅ 2 p0V3 . 2 2 Îòñþäà íàõîäèì 2U0 4U0 V1 = V3 = 3 p0 , 3 p0 . Âèäèì, ÷òî V3 = 2V1 . Ó÷àñòêè öèêëà 12 è 34 èçîõîðû. Äåéñòâèòåëüíî, çàïèøåì óðàâíåíèå ïðÿìîé 12 â âèäå p = αU , ãäå α êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè, èëè 3 2 p = α ⋅ pV , îòêóäà ïîëó÷àåì V = = const . Àíàëîãè÷2 3α íûé âûâîä ñïðàâåäëèâ è äëÿ ó÷àñòêà 34. Ñëåäîâàòåëüíî, V2 = V1 è V4 = V3 . Òîãäà öèêë â êîîðäèíàòàõ ð, V ïðåäñòàâëÿåò ñîáîé óæå âñòðå÷àâøèéñÿ íàì â ïÿòîé çàäà÷å ïðÿìîóãîëüíèê (ðèñ.8). Òåïåðü ïðèñòóïèì ê ðàñ÷åòàì. Ðàáîòà öèêëà ðàâíà Ðèñ. 8  öèêëå 2342 òåïëî ïîäâîäèòñÿ íà ó÷àñòêå 42, à îòâîäèòñÿ íà ó÷àñòêàõ 23 è 34. Ñëåäîâàòåëüíî, η2 = 1 −  öèêëå 12341 òåïëî ïîäâîäèòñÿ íà ó÷àñòêàõ 12 è 4 1, à îòâîäèòñÿ íà ó÷àñòêàõ 23 è 34. Ïîýòîìó η = 1− Q1 = Q12 + Q23 = (U2 − U1 ) + (U3 − U2 ) + A23 = = (U3 − U1 ) + 2 p0V1 = 3 3 13 p0V1 . ⋅ 2 p0 ⋅ 2V1 − p0V1 + 2 p0V1 = 2 2 2 Q23 + Q34 = (1 − η1 )(1 − η2 ) Q41 + Q12 è îêîí÷àòåëüíî ïîëó÷èì η = η1 + η2 − η1η2 . Çàäà÷à 9 (ÌÃÓ, ôèçôàê, 2000). Íà ðV-äèàãðàììå, èçîáðàæåííîé íà ðèñóíêå 10, ïîêàçàíî èçìåíåíèå ñîñòîÿíèÿ ãàçà, èñïîëüçóåìîãî â êà÷åñòâå ðàáî÷åãî âåùåñòâà òåïëîâîãî äâèãàòåëÿ. Îòíîøåíèå ìàêñèìàëüíîé àáñîëþòíîé òåìïåðàòóðû ãàçà ê åãî ìèíèìàëüíîé òåìïåðàòóðå â äàííîì öèêëå ðàâíî 4. Âî ñêîëüêî ðàç îòëè÷àåòñÿ ÊÏÄ η ýòîãî öèêëà îò ìàêñèìàëü- Ðèñ. 10 íî âîçìîæíîãî? Ðåøåíèå. Ïðîèçâåäåíèå ðV äîñòèãàåò íàèáîëüøåãî çíà÷åíèÿ â òî÷êå 2, à íàèìåíüøåãî â òî÷êå 1.  ñèëó óðàâíåíèÿ ÊëàïåéðîíàÌåíäåëååâà, ìàêñèìàëüíàÿ òåìïåðàòóðà ãàçà áóäåò â òî÷êå 2, à ìèíèìàëüíàÿ â òî÷êå 1, ò.å. T2 = 4T1 . Çàïèøåì óðàâíåíèÿ ñîñòîÿíèÿ äëÿ âåðøèí öèêëà: p1V1 = νRT1 , p2V2 = νRT2 , p3V3 = νRT3 . Ó÷òåì, ÷òî òî÷êè 1 è 2 ëåæàò íà ïðÿìîé, ïðîõîäÿùåé ÷åðåç íà÷àëî êîîðäèíàò: p1 = αV1 , p2 = αV2 , è p2V1 = p1V2 . Çíà÷èò, A p0V1 2 η= = = ≈ 15,4% . Q1 (13 2 ) p0V1 13 Çàäà÷à 8 (ÌÔÒÈ). ÊÏÄ öèêëà 1241 ðàâåí η1 , à öèêëà 2342 ðàâåí η2 . Ó÷àñòêè 41 è 23 èçîõîðû, ó÷àñòîê 34 èçîáàðà, ó÷àñòêè 12 è 24 ïðåäñòàâëÿþò ñîáîé ëèíåéíóþ çàâèñèìîñòü äàâëåíèÿ îò îáúåìà (ðèñ.9). Âñå öèêëû îáõîäÿòñÿ ïî ÷àñîâîé ñòðåëêå. Íàéäèòå ÊÏÄ η öèêëà 12341. Ðåøåíèå.  öèêëå 1 241 òåïëî ïîäâîäèòñÿ íà ó÷àñòêàõ 12 è 41, à Ðèñ. 9 îòâîäèòñÿ íà ó÷àñòêå 24. Çíà÷èò, Q1 = Q12 + Q41 , Q2 = Q24 , Q23 + Q34 . Q41 + Q12 Èç ôîðìóë äëÿ η1 è η2 íàéäåì A = p0V1 . Òåïëî ïîäâîäèòñÿ ê ãàçó íà ó÷àñòêàõ 12 è 23, ïîýòîìó Q23 + Q34 . Q24 Èç âñåõ ïîëó÷åííûõ óðàâíåíèé ëåãêî íàéäåì, ÷òî p2 = 2 p1 è T3 = 2T1 . Èçâåñòíî, ÷òî ÊÏÄ ëþáîé òåïëîâîé ìàøèíû, ðàáîòàþùåé â íåêîòîðîì èíòåðâàëå òåìïåðàòóð, íå ìîæåò áûòü áîëüøå ÊÏÄ ìàøèíû, ðàáîòàþùåé ïî öèêëó Êàðíî â òîì æå èíòåðâàëå òåìïåðàòóð.  íàøåì ñëó÷àå T − T1 3 ηmax = 2 = . 4 T2 Íàéäåì òåïåðü ÊÏÄ äàííîãî öèêëà η . Ðàáîòà ãàçà çà öèêë ðàâíà A= 1 (V3 − V1 )( p2 − p3 ) = 1 (V3 p2 − V3 p3 − V1p2 + V1p3 ) = 2 2 = νRT1 1 (νRT2 − νRT3 − νRT1 ) = . 2 2 Î÷åâèäíî, ÷òî ê ãàçó ïîäâîäèòñÿ òåïëî òîëüêî íà ó÷àñòêå 1 2, ïîýòîìó Q1 = Q12 = A12 + (U2 − U1 ) = è Q Q24 η1 = 1 − 2 = 1 − Q1 Q12 + Q41 . 3 3 = ( A + p1 (V3 − V1 )) + νRT2 − νRT1 = 6νRT1 . 2 2 ÏÐÀÊÒÈÊÓÌ Ñëåäîâàòåëüíî, ηmax 0,5νRT1 1 34 η= = = = 9. ,è η 6νRT1 12 1 12 Çàäà÷à 10 («Çàäà÷íèê «Êâàíòà», Ô820). Îïðåäåëèòå ÊÏÄ öèêëà ÀÂÑÀ, èçîáðàæåííîãî íà ðèñóíêå 11. Ðåøåíèå. Ýòà çàäà÷à ìîæåò ïîêàçàòüñÿ âåñüìà ïîõîæåé íà ïåðâóþ, èáî òðåóãîëüíûé öèêë â îáåèõ çàäà÷àõ îäèí è òîò æå, òîëüêî ðàñïîëîæåííûé ïî-ðàçíîÐèñ. 11 ìó. Íî ýòî ñõîäñòâî êàæóùååñÿ, òàê êàê ýòà çàäà÷à ñóùåñòâåííî òðóäíåå ïåðâîé. Ðàáîòà ãàçà çà öèêë îïðåäåëÿåòñÿ ñðàçó: 1 A = p0V0 . 2 À äëÿ íàõîæäåíèÿ ïîäâåäåííîãî êîëè÷åñòâà òåïëîòû Q1 ïðèäåòñÿ íåìàëî ïîòðóäèòüñÿ. Íà ó÷àñòêå À òåïëî áåçóñëîâíî ïîäâîäèòñÿ, è QAB = UB − U A = 3 3 3 ⋅ 2 p0V0 − p0V0 = p0V0 . 2 2 2 Íà ó÷àñòêå ÂÑ äàâëåíèå âñå âðåìÿ ïàäàåò, îáúåì âñå âðåìÿ ðàñòåò, à âîò òåìïåðàòóðà èçìåíÿåòñÿ áîëåå ñëîæíî ñíà÷àëà îíà äî íåêîòîðîé òî÷êè D ðàñòåò, à ïîòîì ïàäàåò, âîçâðàùàÿñü â òî÷êå Ñ ê ïåðâîíà÷àëüíîìó çíà÷åíèþ (â òî÷êå Â). Ýòî îçíà÷àåò, ÷òî òåïëî ïîäâîäèòñÿ ê ãàçó íå íà âñåì ó÷àñòêå ÂÑ, à òîëüêî íà ýòàïå BD. Íàéäåì QBD . Çàïèøåì ïåðâûé çàêîí òåðìîäèíàìèêè äëÿ ìàëîãî êîëè÷åñòâà òåïëîòû: 5 3 3 ∆Q = ∆U + p∆V = ∆ pV + p∆V = p∆V + V ∆p 2 2 2 (ìû èñïîëüçîâàëè ðàâåíñòâî ∆ ( pV ) = p∆V + V ∆p ). Ïðèðàâíèâàÿ ∆Q ê íóëþ, ïîëó÷èì 5 p ∆p =− . 3V ∆V Èç ãðàôèêà íàéäåì 5 p ∆p p p = − 0 , ò.å. 0 = . ∆V V0 3 V V0 Óðàâíåíèå ïðÿìîé ÂÑ ëåãêî ïèøåòñÿ ïî äâóì èçâåñòíûì òî÷êàì: p p = − 0 V + 3 p0 . V0 ÀÁÈÒÓÐÈÅÍÒÀ è η= (1 2 ) p0V0 = 16 ≈ 16,5% A = . Q1 (97 32 ) p0V0 97 Óïðàæíåíèÿ 1. Íà ðèñóíêå 12 ïðåäñòàâëåí öèêë òóðáîðåàêòèâíîãî äâèãàòåëÿ, ñîñòîÿùèé èç äâóõ èçîáàð è äâóõ àäèàáàò. Ïî èçâåñòíûì òåìïåðàòóðàì T1, T2, T3, T4 íàéäèòå ÊÏÄ öèêëà. Ðèñ. 12 Ðèñ. 13 2 (ÌÈÝÒ). Îïðåäåëèòå ÊÏÄ öèêëà, èçîáðàæåííîãî íà ðèñóíêå 13, åñëè èçâåñòíî, ÷òî â íà÷àëüíîì ñîñòîÿíèè 1 òåìïåðàòóðà ãàçà T1 = 300 Ê , îòíîøåíèå îáúåìîâ ãàçà â ñîñòîÿíèÿõ 3 è 2 ðàâíî 2 è ïðè èçîòåðìè÷åñêîì ðàñøèðåíèè ãàç ñîâåðøàåò ðàáîòó À = 5 êÄæ. Êîëè÷åñòâî âåùåñòâà ãàçà ν = 1 ìîëü. 3 (ÌÀÈ, 2003). Êîýôôèöèåíò ïîëåçíîãî äåéñòâèÿ öèêëà 1231 (ðèñ.14) ðàâåí η = 15%. Íàéäèòå ÊÏÄ öèêëà 3543. 4 (ÌÃÓ, ôèçôàê, 1995). Äàâëåíèå ãàçà ìåíÿþò îò Ðèñ. 14 âåëè÷èíû p1 äî âåëè÷èíû p2 â ñîîòâåòñòâèè ñ pV-äèàãðàììîé, èìåþùåé âèä òðåóãîëüíèêà, ïîêàçàííîãî íà ðèñóíêå 15. Íàéäèòå ÊÏÄ öèêëà, åñëè òåìïåðàòóðà ãàçà â ñîñòîÿíèè 3 áîëüøå åãî òåìïåðàòóðû â ñîñòîÿíèè 1. 5 (ÌÀÈ, 2003). Öèêë ñîñòîèò èç èçîõîðû 12, èçîáàðû 23 è ïðÿìîé 31 (ðèñ.16). Òåìïåðàòóðû â òî÷êàõ 1, 2 è 3 ñâÿçàíû ñîîòíîøåíèÿìè T2 = 1,5 T1 è Ðèñ. 15 T3 = 3 T1 . Îïðåäåëèòå ÊÏÄ öèêëà. 6 (ÌÔÒÈ). Öèêë 1231 ñîñòîèò èç ïðÿìîëèíåéíîãî ó÷àñòêà 12, àäèàáàòû 23 è èçîòåðìû 31 (ðèñ.17). Åãî ÊÏÄ ðàâåí Òàêèì îáðàçîì, äëÿ êîîðäèíàò òî÷êè D ïîëó÷àåì p1 = 15 9 p0 , V1 = V0 8 8 (âèäíî, ÷òî p1V1 ëåæèò ìåæäó ñîîòâåòñòâóþùèìè ïðîèçâåäåíèÿìè äëÿ òî÷åê  è Ñ) è íàõîäèì 1 QBD = (UD − UB ) + (2 p0 + p1 )(V1 − V0 ) = 2 = 3 3 1 7 25 49 p1V1 − ⋅ 2 p0V0 + ⋅ ⋅ p0V0 = p0V0 . 2 2 2 8 8 32 Ñëåäîâàòåëüíî, Q1 = QAB + QBD = 3 49 97 p0V0 + p0V0 = p0V0 , 2 32 32 Ðèñ. 16 Ðèñ. 17 η1 . Öèêë 1341 ñîñòîèò èç èçîòåðìû 13, èçîáàðû 34 è àäèàáàòû 41. Åãî ÊÏÄ ðàâåí η2 . Îïðåäåëèòå ÊÏÄ öèêëà 12341. Âñå öèêëû îáõîäÿòñÿ ïî ÷àñîâîé ñòðåëêå.