Зонная структура твердых тел (краткие сведения) m p EE 2 + =
реклама
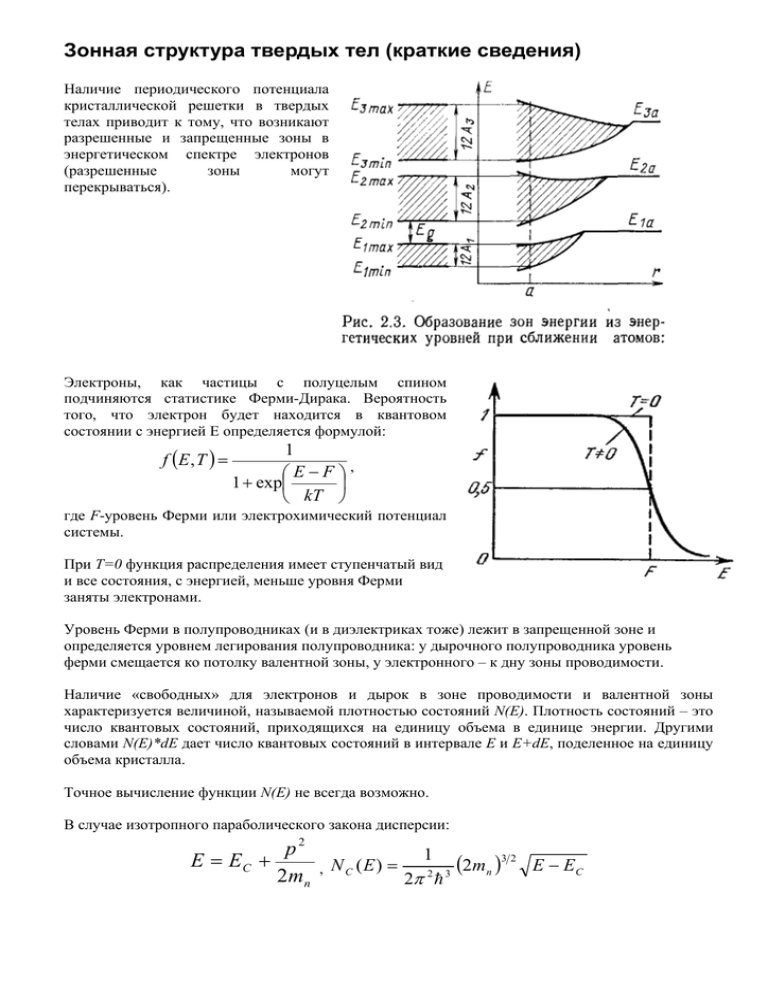
Зонная структура твердых тел (краткие сведения) Наличие периодического потенциала кристаллической решетки в твердых телах приводит к тому, что возникают разрешенные и запрещенные зоны в энергетическом спектре электронов (разрешенные зоны могут перекрываться). Электроны, как частицы с полуцелым спином подчиняются статистике Ферми-Дирака. Вероятность того, что электрон будет находится в квантовом состоянии с энергией E определяется формулой: f (E , T ) = 1 ⎛E−F⎞, 1 + exp⎜ ⎟ ⎝ kT ⎠ где F-уровень Ферми или электрохимический потенциал системы. При T=0 функция распределения имеет ступенчатый вид и все состояния, с энергией, меньше уровня Ферми заняты электронами. Уровень Ферми в полупроводниках (и в диэлектриках тоже) лежит в запрещенной зоне и определяется уровнем легирования полупроводника: у дырочного полупроводника уровень ферми смещается ко потолку валентной зоны, у электронного – к дну зоны проводимости. Наличие «свободных» для электронов и дырок в зоне проводимости и валентной зоны характеризуется величиной, называемой плотностью состояний N(E). Плотность состояний – это число квантовых состояний, приходящихся на единицу объема в единице энергии. Другими словами N(E)*dE дает число квантовых состояний в интервале E и E+dE, поделенное на единицу объема кристалла. Точное вычисление функции N(E) не всегда возможно. В случае изотропного параболического закона дисперсии: p2 1 E = EC + (2mn )3 2 E − EC , N C (E) = 2 3 2m n 2π h p2 1 32 E = EV − ( 2m p ) EV − E , NC (E) = 2 3 2m p 2π h Согласно вышесказанному, концентрация электронов в зоне проводимости равна ∞ n = ∫ N C ( E ) f (E , t )dE , p = Ec Ev ∫N V ( E ) f (E , t )dE −∞ Для невырожденного полупроводника (уровень ферми лежит в запрещенной зоне и отступает от краев зона на 2-3 kT) с примесью одного типа, выражения для концентрации электронов в зоне проводимости и дырок в валентной зоне принимают вид: ⎛ F − Ec ⎞ n = N c exp⎜ ⎟ , p = N v exp⎛⎜ Ev − F ⎞⎟ , ⎝ kT ⎠ ⎝ kT ⎠ где Nc, Nv – эффективные плотности состояний в C и V зонах. Подробнее смотрите в учебнике Шалимова К.В. Физика полупроводников, Энергоатомиздат, 1985 г. - 392 с.