Ваганова А.С. Задачи типа С2. В кубе ABCDA В
реклама

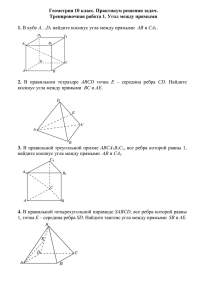
Ваганова А.С. Задачи типа С2. 1. В кубе ABCDA1B1C1D1 точка Е - середина ребра А1В1. Найдите синус угла между прямой АЕ и плоскостью BDD1. Ответ: 2. В кубе ABCDA1B1C1D1 точка Е - середина ребра А1В1. Найдите синус угла между прямой АЕ и плоскостью BDC1. Ответ: 3. В правильной шестиугольной призме А…F1, все рёбра которой равны 1, точка G- середина ребра А1В1. Найдите синус угла между прямой AG и плоскостью BDD1. Ответ: 4. В правильной треугольной призме A…С1, все рёбра которой равны 1, точки D,Е – середины рёбер соответственно А1В1 и А1С1. Найдите тангенс угла между плоскостями АDE и BCC1. Ответ: 5. В правильной шестиугольной пирамиде SАBCDEF, стороны основания которой равны 1, а боковые стороны равны 2, найдите синус угла между прямыми AL и BM, где M- середина ребра SC, L- середина ребра SB. Ответ: 6. В правильной треугольной пирамиде SABC c основанием АВС проведено сечение через вершину S и середины рёбер АВ и ВС. Найдите расстояние от плоскости этого сечения до центра грани SAC, если все рёбра пирамиды равны 6. Ответ: 2. 7. В правильной шестиугольной пирамиде SАBCDEF сторона основания равна 1, боковое ребро равно 2. Найдите угол между плоскостями АВS и SDC. Ответ: 8. В правильной треугольной пирамиде SABC с вершиной S на сторонах АВ и АС выбраны точки М и К соответственно так, что треугольник АМК подобен треугольнику АВС с коэффициентом подобия . На прямой МК выбрана точка Е так, что МЕ:ЕК=7:9. Найти расстояние от точки Е до плоскости BSC, если сторона основания пирамиды равна 6, а высота равна . Ответ: 9. В правильной четырёхугольной пирамиде SABCD с вершиной S, со стороной основания и боковым ребром 5 найти угол между прямой АВ и плоскостью, проходящей через середины ВС и DC и вершину S. Ответ: 10. Cфера с центром О вписана в прямоугольный параллелепипед А…D1. Найдите угол между прямыми В1О и ВК, где К-середина DC. Ответ: