1) Точка
реклама

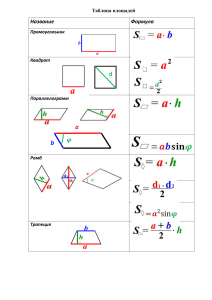
Лекция № 1 Многогранники. Выпуклые многогранники. Правильные многогранники. ГЕОМЕТРИЯ ПЛАНИМЕТРИЯ СТЕРЕОМЕТРИЯ Планиметрия — раздел геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Фигуры, изучаемые планиметрией: 1. Точка 2. Прямая 3. Параллелограмм (частные случаи: квадрат, прямоугольник, ромб) 4. Трапеция 5. Окружность 6. Треугольник 7. Многоугольник 1) Точка: Точка — это одно из фундаментальных понятий геометрии, поэтому "точка" не имеет определения. 2) Прямая: Прямая — одно из основных понятий геометрии. Геометрическая прямая (прямая линия) — незамкнутый с двух сторон, протяженный не искривляющийся геометрический объект, поперечное сечение которого стремится к нулю, а продольная проекция на плоскость даёт точку. 3) Параллелограмм Параллелограмм — это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Частные случаи: Квадрат — правильный четырёхугольник или ромб, у которого все углы прямые, или параллелограмм, у которого все стороны и углы равны. Квадрат может быть определён как: прямоугольник, у которого две смежные стороны равны ромб, у которого все углы прямые (любой квадрат является ромбом, но не любой ромб является квадратом). Прямоугольник — это параллелограмм , у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу теоремы о сумме углов многоугольника) также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360° - прямоугольников не существует. Ромб — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом. 4) Трапеция Трапеция — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция. Прямоугольная трапеция Равнобокая трапеция 5) Окружность Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом. 6) Треугольник Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки. Если все три точки треугольника лежат на одной прямой, он называется вырожденным. 7) Многоугольник — это геометрическая фигура, определяется как замкнутая ломаная. Существуют три различных варианта определения: Плоские замкнутые ломаные; Плоские замкнутые ломаные без самопересечений; Части плоскости, ограниченные ломаными. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника. Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. Многогранник – это геометрическое тело, ограниченное сторон плоскими многоугольниками, называемыми гранями. со всех Название многогранника зависит от основания и боковых рёбер. Правильный многогранник, многогранник, все грани которого — одинаковые правильные многоугольники и все многогранные углы при вершинах равны между собой. Существует пять видов выпуклых правильных тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. многогранников: Тетраэдр – это простейший многогранник, гранями которого являются четыре треугольника (правильная треугольная пирамида). Куб – это правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы. Октаэдр – один из пяти выпуклых правильных многогранников, так называемых Платоновых тел. Октаэдр – это Тело, ограниченное восемью треугольниками; восьмигранник. Додекаэдр – это двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Икосаэдр - правильный выпуклый многогранник, составленный из 20 правильных треугольников.