Планы проведения дополнительных занятий по подготовке к ЕГЭ

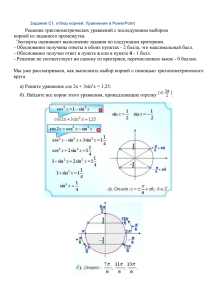
Планы проведения дополнительных занятий по подготовке к ЕГЭ
в 11
классе по математике.
Выполнил учитель МБОУ СОШ №46 пгт Черноморского МО Северский
район
Билько Владимир Николаевич
Тема: Решение тригонометрических уравнений ( задача №15)
Занятие №1.
1.Теоретический материал. Обращаю внимание учащихся на то, что не
обязательно заучивать все тригонометрические формулы, потому что это
довольно трудно (всего не упомнишь). Важно запомнить идею получения
этих формул. Но Формулы сложения запомнить нужно.
1)
2)
3)
4)
Из них легко получить
Формулы двойного угла
1)
2)
2.Решение уравнений фронтально. №1
№2а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение:
Решение
3. Работа в группах .Решение уравнений
Первая группа
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Решение
Упростим второе слагаемое с помощью формул приведения):
Получим:
Первое слагаемое по основному тригонометрическому тождеству приведем к выражению
с синусом:
Приведем подобные и домножим на -1:
Получили квадратное относительно
уравнение, решение которого
Первое решение не имеет корней, поскольку синус принимает значения от -1 до 1
(Область определения и множество значений тригонометрических функций)
Второе является простейшим тригонометрическим
Получили ответ на пункт А.
Теперь укажем какие корни попадут в промежуток
Сделаем отбор на единичной окружности
В указанный промежуток попадают корни
Обратите внимание на то, что -3pi находится на втором обороте по часовой стрелке, и на
единичной окружности его расположение совпадает с -pi.
Ответ:
а)
б)
Вторая группа а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Задание для самостоятельной работы дома:
Дано уравнение
.
а) Решите данное уравнение.
б) Укажите корни данного уравнения, принадлежащие промежутку
.
Решение
.
Отсюда
Если
Если
или
.
, то
.
, то
.
Из найденных решений промежутку
принадлежат числа
и
.
Ответ: а)
; б)
.
Данное задание представляется c первого раза очень любопытным. В этом уравнении
кажется сконцентрированы очень присущие черты ЕГЭ по математике.
Занятие №2
1. Теоретический материал. Повторение формул приведения.
2. Свойства логарифмов:
3. 1°
4.
5.
6.
7.
8.
основное
логарифмическое тождество.
2°
3°
Логарифм единицы по любому
положительному, отличному от 1,
основанию равен
нулю.
Это
возможно потому, что из любого
действительного числа можно
получить 1 только возведя его в
нулевую степень.
4°
логарифм произведения.
Логарифм произведения равен
сумме логарифмов сомножителей.
9. 5°
логарифм частного.
10. Логарифм частного (дроби) равен
разности
логарифмов
сомножителей.
11. 6°
логарифм степени.
12. Логарифм
степени
равен
произведению показателя степени
на логарифм ее основания.
13. 7°
14. 8°
15. 9°
- переход к
новому основанию.
3 Решение уравнений фронтально
а) Решите уравнение
.
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решим уравнение:
.
Отберём корни, принадлежащие отрезку
рис.):
. Это числа (см.
.
Ответ:
A)
Б)
.
.
4.Решение самостоятельно a) 4sin42x+3cos4x–1=0 решите уравнение
б) Отберите корни на промежутке [π; 3π/2]
Проверка самостоятельной работы
5.Задание для самостоятельной работы дома.
1.а) Решите уравнение
.
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
а) Левая часть уравнения определена при
Числитель дроби должен быть равен :
, то есть при
.
Серию
нужно отбросить. Получаем ответ:
б)
При помощи тригонометрической окружности отберём корни,
лежащие на отрезке
О т в е т : а)
б)
2. Решите систему:
Решение.
Решим первое уравнение. Пусть
Уравнение
Тогда уравнение примет вид:
не имеет решений. Из уравнения
Из второго уравнения системы следует, что
Найдём из второго уравнения:
значит,
находим:
откуда
Поэтому
Ответ:
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
а) Если
то из уравнения следует, что
что противоречит основному тригонометрическому тождеству. Поэтому
отличен от 0, и на него можно поделить обе части уравнения:
б) При помощи тригонометрической окружности отберём корни уравнения, принадлежащие промежутку
О т в е т : а)
:
б)