Лабораторная работа № 15. OПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА

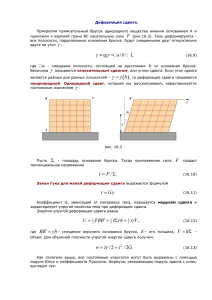
Лабораторная работа № 15.
OПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА С ПОМОЩЬЮ
КРУТИЛЬНОГО МАЯНИКА
Цель работы: определить экспериментально модуль сдвига проволоки
методом крутильных колебаний.
Краткая теория.
1. Деформация кручения
Деформация кручения возникает в образце при действии на него
моментов закручивающих усилий. Пусть верхнее основание однородного упругого образца в форме кругового цилиндра закреплено неподвижно, а к нижнему приложены касательные усилия, распределенные по
 основанию, которые условно можно представить парой
 всему
сил F и  F , как показано на рис.1.
Рис. 1.
Длина образца L , а радиус основания R . Под действием закручивающих усилий нижнее основание цилиндра поворачивается относительно верхнего на угол  , который является абсолютной деформацией кручения.
Угол кручения  , различный для разных сечений цилиндра не
может служить характеристикой деформации кручения цилиндра в
целом. Поэтому вводят в качестве характеристики величины деформации кручения относительную деформацию  / L . Отношение угла
кручения сечения к расстоянию до него от верхнего, закрепленного,
сечения, является постоянной величиной для всех сечений цилиндра.
По закону Гука
1

(1)
 cM ,
L
где c – коэффициент кручения, определяемый свойствами образца,
M – момент закручивающих сил, приложенных к нижнему основанию, относительно оси симметрии образца.
Величина f  1 c обратная коэффициенту кручения, называется модулем кручения. С учетом этого:
M f

,
(2)
L
Проведем в верхнем сечении образца отрезок длины  . Вертикальное сечение цилиндра, проведенное через этот отрезок, при закручивании образца смещается на угол  . Следовательно, при деформации
кручения одновременно происходит сдвиг слоев образца. По закону
Гука угол сдвига равен:
P
(3)
 S,
N
где PS – касательное усилие, приложенное к нижнему основанию, N
– модуль сдвига материала образца.
Угол сдвига можно получить и из геометрических соображений
(рис. 1):


,
(4)
L
Сравнивая (3) и (4), получим выражение для касательного усилия, вызывающего закручивание нижнего основания на угол  :
N
.
(5)
PS 
L
Как видно из (5), величина распределенных по основанию сил и,
соответственно, моментов сил зависят от расстояния до центра основания. Для вычисления полного момента сил, приложенных ко всему
основанию, сначала необходимо определить момент сил, приложенных к малому элементу основания. В качестве такого элемента выберем малый участок кольца радиуса  и ширины d , видимый из центра основания под углом d , как это показано на рис.2.
К выделенному элементу основания приложена элементарно
малая сила
 2N
dF  PS dS 
dd ,
L
2
момент которой относительно центра основания равен
 3N
dM  dF   
dd .
L
(6)
Рис. 2
Полный момент сил, приложенных ко всему основанию, получим путем интегрирования (6):
R
R 2
N  4 2 R 4N 
M    dM 

 

(7)
L 4 0 0
2
L
0 0
Сравнивая полученное выражение для момента сил с законом
Гука (2), получим связь модулей сдвига и кручения:
NR 4
f 
.
2
2. Крутильные колебания.
Пусть верхний конец проволоки 1 радиуса R и длины L закреплен неподвижно, а к нижнему ее концу крепится в специальном
подвесе 2 тело 3, как это показано на рис.3. Момент инерции системы
относительно оси проволоки равен I .
Если повернуть тело на малый угол  , в проволоке возникают
упругие силы, момент которых по величине равен:
 NR 4
M 
.
2L
Учитывая направления момента сил и угла поворота, получим:
NR 4
M 
.
(9)
2L
3
Рис. 3.
Если систему вывести из положения равновесия и затем предоставить самой себе, она начнет совершать колебания. Пусть в произвольный момент времени угол отклонения от положения равновесия
равен  , тогда по уравнению моментов
d 2
NR 4
I 2 
,
(10)
dt
2L
или
d 2 NR 4

  0.
(11)
dt 2
2 IL
Уравнение (II) представляет собой дифференциальное уравнение гармонических колебаний, решением которого является гармоническая функция:
   0 sin t   0 
(12)
Круговая частота этих колебаний равна:
NR 4
,
(13)

2 LI
а период колебаний определяется соотношением
2
2 LI
T
 2
.
(14)

NR 4
3. Метод определения модуля сдвига с помощью крутильного маят-
4
ника.
Если в системе, описанной выше, измерить период колебаний,
то из (14) следует, что:
8LI
(15)
N 4 2
RT
Момент инерции системы состоит из момента инерции тела, проволоки и подвеса. Момент инерции тела правильной формы несложно рассчитать, чего нельзя сказать о моменте инерции подвеса относительно
сложной формы, для того, чтобы исключить из расчетов момент
инерции подвеса, поступают следующим образом. Пусть в подвесе,
момент инерции которого вместе с проволокой равен I 0 , закреплено
тело с моментом инерции I 1 относительно оси проволоки. Период колебаний системы в этом случае равен:
2I 0  I1 L
(16)
T1  2
NR 4
Если затем закрепить тело в подвесе так, что его момент инерции относительно оси проволоки станет равным I 2 , период колебаний
системы изменится:
2I 0  I 2 L
(17)
T2  2
NR 4
Из (16) и (17), исключая неизвестное значение I 0 , получим
8LI  I 
(18)
N  4 21 22
R T1  T2 
Если тело представляет собой прямоугольный параллелепипед массы
m и ребрами длиной a, b, c , (рис.4), то моменты инерции его относительно осей OX , OY , OZ , проходящих через центр масс тела, соответственно равны:
m
I X  b 2  c 2 ,
12
m
I Y  a 2  c 2 ,
12
m
I Z  b 2  a 2 .
12
5
Рис.4
Проводя измерения, закрепляем тело в подвесе относительно
осей OX, OZ и измеряем периоды колебаний T1 ,T2 . Тогда выражение
(18) можно записать в виде:
2mLa 2  c 2 
N
,
(19)
3R 4 T12  T22 
где T1 ,T2 – периоды колебаний относительно осей OX, OZ , R – радиус проволоки.
Учитывая, что проволоки две, момент сил удваивают. Поэтому
формула (19) примет вид:
mL' a 2  c 2 
N
(19’)
6 R 4 T12  T22 
где L'  L  L1 , или, при L  L1 :
mLa 2  c 2 
N 4 2
(19’’)
3R T1  T22 
Измерения
1. Измерить радиус проволоки R и ее длину L , результаты измерений занести в таблицу.
2. Измерить линейные размеры тела, закрепленного в подвесе, результаты измерений и значение массы тела внести в таблицу.
3. Закрепить тело в подвесе, как это описано выше.
4. Включить прибор, нажав кнопку "Сеть", кнопка "Пycк" должна
быть при этом выключена.
5. Повернуть подвес так, чтобы его притянул электромагнит, нажать
кнопку "Сброс".
6. Нажать кнопку "Пycк" при появлении на индикаторе числа перио-
6
дов цифры "9" нажать кнопку "Стоп". Прибор зафиксирует время
десяти полных периодов колебаний. Результаты измерений периода колебаний внести в таблицу. Измерения провести не менее 10
раз.
7. Повторить измерения для другого положения тела в подвесе, как
это указано в п.п.5-6.
8. Выключить прибор, нажав кнопку "Сеть", освободить тело из подвеса.
9. Рассчитать модуль сдвига по (19).
10.Рассчитать погрешность измерения модуля сдвига.
1.
2.
3.
4.
Контрольные вопросы
Выведите связь между модулями кручения и сдвига.
Объясните сущность методов определения модуля сдвига.
Каков физический смысл модулей сдвига и кручения?
Рассчитайте момент инерции прямоугольного параллелепипеда относительно осей, проходящих через центр масс тела перпендикулярно его граням.
7