лабораторная работа м–5 определение модуля сдвига
реклама

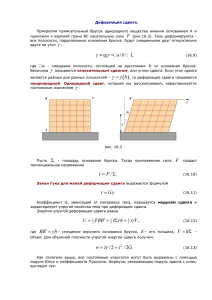
ЛАБОРАТОРНАЯ РАБОТА М–5 ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ДИНАМИЧЕСКИМ МЕТОДОМ ОБОРУДОВАНИЕ: крутильный маятник, технические весы, секундомер, микрометр, линейка. Под влиянием внешних сил всякое тело изменяет свою форму и размеры, т.е. деформируется. Упругой называется деформация, исчезающая с прекращением действия силы. Существуют различные типы деформации: растяжение (сжатие), сдвиг, кручение. ДЕФОРМАЦИЯ СДВИГА Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 1). Â Ñ Â1 Ñ1 F X l À Ä Рис. 1 Сдвиг твердого тела Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно. Так как угол мал, формулу можно записать в виде: γ tgγ CC1 , CD (1) где СС1 = X – абсолютный сдвиг, – угол сдвига, называемый также относительным сдвигом, выражается в радианах. 1 По закону Гука относительный сдвиг пропорционален касательному напряжению F/S, где S – площадь поверхности грани ВС, т.е. F Nγ , S (2) где N – модуль сдвига. N F . γS (3) Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется). ДЕФОРМАЦИЯ КРУЧЕНИЯ Если проволоку или стержень, закрепленные с одного конца, закручивать, прилагая к другому концу пару сил F с моментом, равным М, то стержень (проволока) претерпевает деформацию кручения, при которой одно его основание поворачивается по отношению к другому, фиксированному, на некоторый угол – угол кручения. По закону Гука: f M . φ (4) Модуль кручения f показывает, какой момент силы нужно приложить, чтобы закрутить проволоку на угол в 1 рад. В результате деформации кручения возникает перекос образующих цилиндрической поверхности стержня (рис. 2), причем rφ γl . (5) Поэтому расчет деформации кручения может быть сведен к расчету деформации сдвига. Приведем без вывода соотношение, существующее между модулем кручения f и модулем сдвига N материала проволоки 2 F Ì î F l Î / Рис. 1 Деформация кручения f πr 4 N , 2l (6) где r, l – соответственно радиус и длина проволоки. Из формулы (6) имеем N 2lf . πr 4 (7) Таким образом, модуль сдвига можно найти, зная модуль кручения. Динамический метод измерения модуля кручения основан на зависимости периода Т крутильных колебаний маятника, подвешенного на проволоке, от упругих свойств материала проволоки. Крутильным маятником служит рейка К с надетыми на нее цилиндрическими грузами Р, подвешенная на проволоке длиной l (см. рис. 3). 3 Если колеблющиеся тела совершают вращательное движение, то к ним может быть применен основной закон динамики вращательного движения M βJ J dω d2 J 2 , dt dt (8) где М – вращающий момент относительно оси АВ, J – момент инерции тела относительно той же оси, d dω d 2 ω – угловое ускорение, 2 . dt dt dt Учитывая (4), (8) можно переписать в виде J d 2φ fφ. dt 2 (9) Знак минус говорит о том, что вращающий момент сдвига направлен так, чтобы уменьшить угловое отклонение. r L l1 P P l2 Рис. 2 Таким образом, тело совершает гармонические колебания, периоды которых можно найти из условия, что множитель пропорциональности 4 d 2φ и в уравнении (9) в данном случае 1/J должен быть равен dt 2 4π 2 f 4π 2 ω 2 2 , т.е. 2 , откуда J T T между T 2 J , f (10) где Т – период колебания маятника. Чтобы найти f, необходимо исключить неизвестный момент инерции J. Для этого в задаче определяются два периода колебаний маятника. Используя возможность передвижения груза Р на рейке установки, меняем расстояние от оси вращения. В соответствии с l1 и l2 получаем моменты инерции J1 и J2. J1 J 0 2ml12 (11) J 2 J 0 2ml 22 , где J0 – момент инерции рейки крутильного маятника. Периоды колебаний будут соответственно равны T1 2 π J 0 2ml12 f (12) J 2ml 22 T2 2 π 0 . f Решая совместно два последних уравнения, получим формулу для расчета модуля кручения проволоки крутильного маятника: f 8π 2 m l12 l22 . T12 T22 (13) Используя формулу (7), по модулю кручения f рассчитываем модуль сдвига N. ЗАДАНИЕ И ОТЧЕТНОСТЬ Закрепите грузы Р, предварительно определив их массу взвешиванием, на расстоянии l1 от центра маятника. Измерьте секундомером время 10-15 полных колебаний. Определите период Т1. 1. Передвиньте грузы на рейке на расстоянии l2 , определите Т2. 2. Определите модуль кручения f по формуле (13). 5 3. Измерьте микрометром радиус r проволоки крутильного маятника и определите его длину L. 4. По формуле (7) определите модуль сдвига N. 5. Результаты измерений занесите в таблицу 1. Таблица 1 t, №№ l 10-15 колебаний Т m f r L N 1 2 КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Что называется деформацией? Виды деформации. 2. Силы упругости. Закон Гука. 3. Деформация кручения. Модуль кручения. Связь между модулем сдвига и модулем кручения. 4. Каков физический смысл модуля кручения, модуля сдвига? 5. Метод определения модуля кручения в данной работе. РАСЧЕТЫ И ВЫВОДЫ 6