zanyatie47_EGE_Geometricheskiy_smysl_proizvodnoy ()
реклама
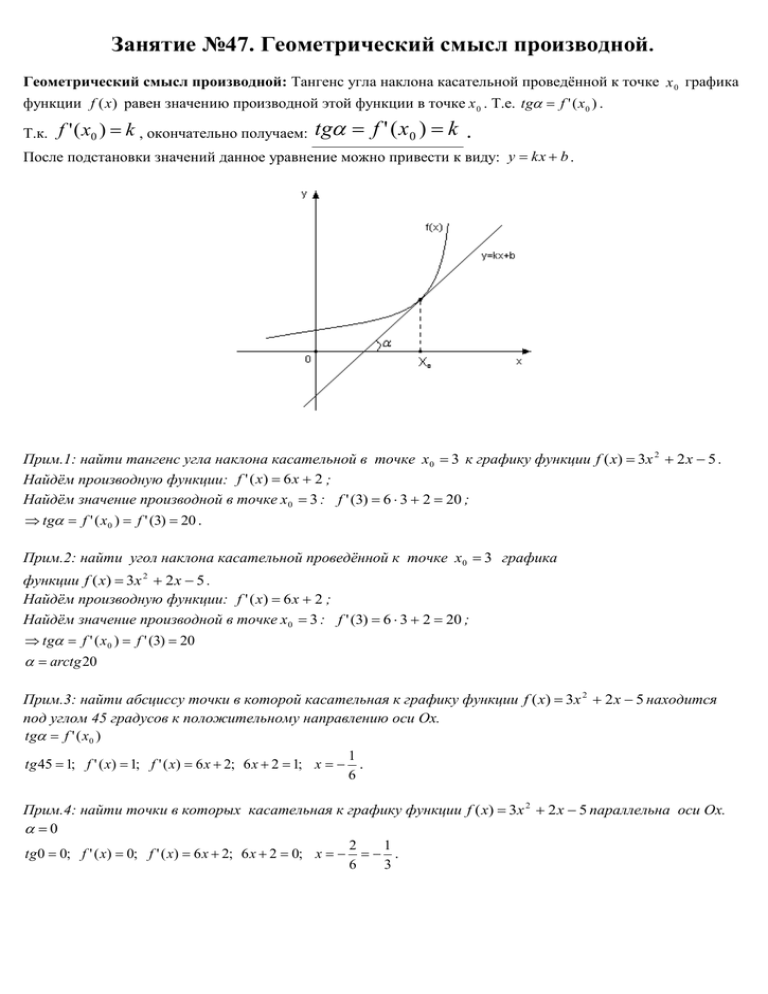
Занятие №47. Геометрический смысл производной. Геометрический смысл производной: Тангенс угла наклона касательной проведённой к точке x 0 графика функции f (x) равен значению производной этой функции в точке x 0 . Т.е. tg f ' ( x0 ) . Т.к. f ' ( x0 ) k , окончательно получаем: tg f ' ( x 0 ) k . После подстановки значений данное уравнение можно привести к виду: y kx b . Прим.1: найти тангенс угла наклона касательной в точке x 0 3 к графику функции f ( x) 3x 2 2 x 5 . Найдём производную функции: f ' ( x) 6 x 2 ; Найдём значение производной в точке x 0 3 : f ' (3) 6 3 2 20 ; tg f ' ( x 0 ) f ' (3) 20 . Прим.2: найти угол наклона касательной проведённой к точке x 0 3 графика функции f ( x) 3x 2 2 x 5 . Найдём производную функции: f ' ( x) 6 x 2 ; Найдём значение производной в точке x 0 3 : f ' (3) 6 3 2 20 ; tg f ' ( x 0 ) f ' (3) 20 arctg 20 Прим.3: найти абсциссу точки в которой касательная к графику функции f ( x) 3x 2 2 x 5 находится под углом 45 градусов к положительному направлению оси Ох. tg f ' ( x0 ) 1 tg 45 1; f ' ( x) 1; f ' ( x) 6 x 2; 6 x 2 1; x . 6 Прим.4: найти точки в которых касательная к графику функции f ( x) 3x 2 2 x 5 параллельна оси Ох. 0 2 1 tg 0 0; f ' ( x) 0; f ' ( x) 6 x 2; 6 x 2 0; x . 6 3 1. Найти тангенс угла наклона касательной в точке x 0 3 к графику функции: 1) 2) f ( x) f ( x) 4 x 2 x ; 1 2x 5 ; 3 3) f ( x) 2. Найти тангенс угла наклона касательной в точке x 0 1) f ( x) cos 3 x ; 2) f ( x) 3 sin 2 x ; x x 5 ; 4) f ( x) 3x 4 3x 2 5 ; x3 3 : 3) f ( x) 2ctg(3x) ; 4) f ( x) tg 2 x ; 3. Найти тангенс угла наклона касательной в точке x 0 0 : 1) f ( x) 3e 3 x ; 4) f ( x) 5 x ; 2) f ( x) 0.5 ln x ; 3) f ( x) 6 log 5 x ; 4. Найти абсциссу точки в которой касательная к графику функции находится под углом 45 градусов к положительному направлению оси Ох. 5 x 1 ; 2) f ( x) ; 3 x6 5. Найти абсциссу точки в которой касательная к графику функции параллельна оси Ох. 1) f ( x) 1) f ( x) 2x 1 ; 2) f ( x) 7 x 2 x ; x 2x 1 2 Домашнее задание: 1. Найти тангенс угла наклона касательной в точке x 0 0 к графику функции: 1) f ( x) 2 x 4 x 2 x ; 3 2 2) f ( x) 3 2 x 2 ; 3) f ( x) 2. Найти тангенс угла наклона касательной в точке x 0 1) f ( x) 5 sin x ; 2 3x 2 ; 4) f ( x) 7 x x 3 6 ; x2 к графику функции: 2) f ( x) 2 cos x 1 ; 3. Найти абсциссу точки в которой касательная к графику функции находится под углом 45 градусов к положительному направлению оси Ох. 1) f ( x) 2 ; 5 x 2) f ( x) x6 ; 3 4. Найти абсциссу точки в которой касательная к графику функции параллельна оси Ох. 1) f ( x) x 2 2 x 1 ; 2) f ( x) 2 x 2 x ;



