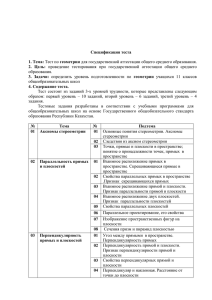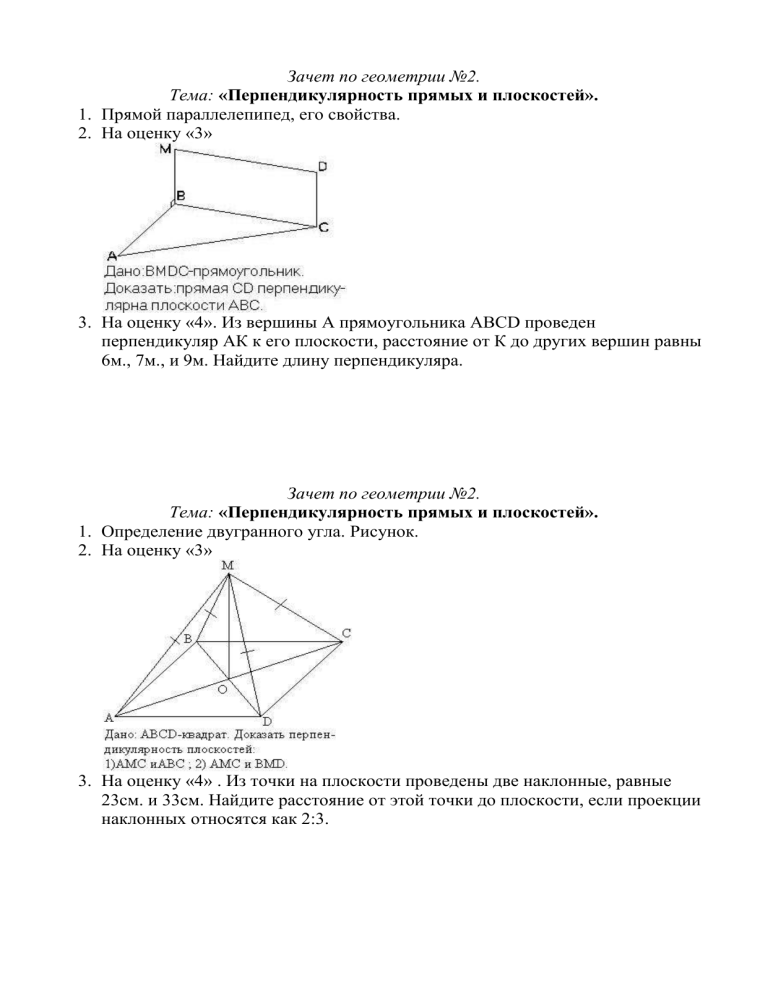
Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Прямой параллелепипед, его свойства. 2. На оценку «3» 3. На оценку «4». Из вершины А прямоугольника АВСD проведен перпендикуляр АК к его плоскости, расстояние от К до других вершин равны 6м., 7м., и 9м. Найдите длину перпендикуляра. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Определение двугранного угла. Рисунок. 2. На оценку «3» 3. На оценку «4» . Из точки на плоскости проведены две наклонные, равные 23см. и 33см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Определение перпендикуляра к плоскости, наклонной и проекции наклонной на плоскость. Рисунок. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD-квадрат. Докажите, что плоскости (АСС1) и (ВВ1D1) взаимно перпендикулярны. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Определение угла между прямой и плоскостью. Рисунок. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD-квадрат, AD=2см., АС1= 2 6 см. Найдите СС1. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Сформулируйте лемму о двух параллельных прямых, перпендикулярных третьей прямой. 2. На оценку «3» 3. На оценку «4». Из вершины А прямоугольника АВСD проведен перпендикуляр АК к его плоскости, расстояние от К до других вершин равны 6м., 7м., и 9м. Найдите длину перпендикуляра. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Определение перпендикулярных прямых. Рисунок. 2. На оценку «3» 3. На оценку «4» . Из точки на плоскости проведены две наклонные, равные 23см. и 33см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Определение прямой, перпендикулярной плоскости. Рисунок. 2. На оценку «3» 3. В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD-квадрат. Докажите, что плоскости (АСС1) и (ВВ1D1) взаимно перпендикулярны. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Теорема о двух параллельных прямых, одна из которых перпендикулярна плоскости. Докажите. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD-квадрат, AD=2см., АС1= 2 6 см. Найдите СС1. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Теорема о двух прямых, перпендикулярных плоскости. Докажите. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1, AD=12см., CD=5см., А1С=15см. Найдите углы между А1С и (АВС) и между А1С и (ВВ1С1). Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Признак перпендикулярности прямой и плоскости. Докажите. 2. На оценку «3» 3. На оценку «4». Из вершины А прямоугольника АВСD проведен перпендикуляр АК к его плоскости, расстояние от К до других вершин равны 6м., 7м., и 9м. Найдите длину перпендикуляра. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Теорема о существовании и единственности прямой, перпендикулярной плоскости. Докажите. 2. На оценку «3» 3. На оценку «4». Дан △АВС, ∠ С=90°, ∠ А=30°, АС=а, МС перпендикулярен (АВС), МС= a 3 /2. Найдите расстояние от точки М до АВ. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Теорема о трех перпендикулярах. Докажите. 2. На оценку «3» 3. На оценку «4» . Из точки на плоскости проведены две наклонные, равные 23см. и 33см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Признак перпендикулярности плоскостей. Докажите. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1, AD=12см., CD=5см., А1С=15см. Найдите углы между А1С и (АВС) и между А1С и (ВВ1С1). Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Теорема о диагонали прямоугольного параллелепипеда. Докажите. 2. На оценку «3» 3. На оценку «4». Из вершины А прямоугольника АВСD проведен перпендикуляр АК к его плоскости, расстояние от К до других вершин равны 6м., 7м., и 9м. Найдите длину перпендикуляра. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Диагональ квадрата перпендикулярна к некоторой плоскости. Как расположена другая диагональ квадрата по отношению к этой плоскости? Объясните. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1 основание ABCD-квадрат, AD=2см., АС1= 2 6 см. Найдите СС1. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Можно ли через любую точку пространства провести три плоскости, каждые две из которых взаимно перпендикулярных? Объясните и сделайте рисунок. 2. На оценку «3» 3. На оценку «4». Дан △АВС, ∠ С=90°, ∠ А=30°, АС=а, МС перпендикулярен (АВС), МС= a 3 /2. Найдите расстояние от точки М до АВ. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Могут ли две плоскости, каждая из которых перпендикулярна к третьей плоскости быть а) параллельными; б) перпендикулярными? Объясните и сделайте рисунок. 2. На оценку «3» 3. На оценку «4» . Из точки на плоскости проведены две наклонные, равные 23см. и 33см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Верно ли утверждение, что все прямые, перпендикулярные к данной плоскости и пересекающие данную прямую, лежат в одной плоскости? Объясните и сделайте рисунок. 2. На оценку «3» 3. На оценку «4». В прямоугольном параллелепипеде ABCDA1B1C1D1, AD=12см., CD=5см., А1С=15см. Найдите углы между А1С и (АВС) и между А1С и (ВВ1С1). Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Прямая a параллельна плоскости α, а прямая b перпендикулярна к этой плоскости. Существует ли прямая, перпендикулярная к прямым a и b? Объясните и сделайте рисунок. 2. На оценку «3» 3. На оценку «4». Из вершины А прямоугольника АВСD проведен перпендикуляр АК к его плоскости, расстояние от К до других вершин равны 6м., 7м., и 9м. Найдите длину перпендикуляра. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Прямая а параллельна плоскости α, а прямая b перпендикулярна к этой плоскости. Верно ли утверждение, что прямые a и b взаимно перпендикулярны? Объясните и сделайте рисунок. 2. На оценку «3» 3. На оценку «4» . Из точки на плоскости проведены две наклонные, равные 23см. и 33см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3. Зачет по геометрии №2. Тема: «Перпендикулярность прямых и плоскостей». 1. Параллельные прямые b и c лежат в плоскости α, а прямая a перпендикулярна к прямой b. Верно ли утверждение: а) прямая a перпендикулярна прямой c; б) прямая a пересекает плоскость α? Объясните и сделайте рисунок. 2. На оценку «3» 3. На оценку «4». Дан △АВС, ∠ С=90°, ∠ А=30°, АС=а, МС перпендикулярен (АВС), МС= a 3 /2. Найдите расстояние от точки М до АВ. Задачи к зачету по геометрии №2. На оценку «5»: 1. Точка М удалена от каждой стороны равнобедренной трапеции на расстояние, равное 12см. Основания трапеции равны 18см. и 32см. Найдите расстояние от точки М до плоскости трапеции. 2. Концы отрезка АВ=25см. лежат на гранях двугранного угла, равного 60°. Из точек А и В опущены перпендикуляры AC и BD на ребро двугранного угла, АС=5см.,BD=8 см. Найдите CD. 3. ABCD-квадрат, О-точка пересечения диагоналей, ОМ перпендикулярен (АВС), ОМ=3см. Сторона квадрата равна 4 2 см. Найдите угол между плоскостями (ВМС) и (DMC). 4. Дан квадрат ABCD со стороной, равной 1, МВ перпендикулярен (АВС), МВ=1. Найдите расстояние между прямыми AC и MD. 5. Основанием прямого параллелепипеда ABCDA1B1C1D1 служит ромб ABCD. Угол между ребром АА1 и диагональю В1D равен 60°, а расстояние между ними равно 3см. Расстояние между диагональю основания АС и B1D равно 2см. Найдите площадь полной поверхности (сумму площадей всех граней) параллелепипеда.