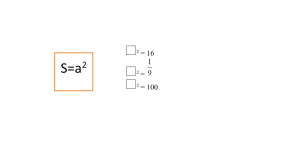
: Свойства арифметического квадратного корня.

Учитель математики:
Сейфуллина Э.В.
Тема урока:
Свойства арифметического
квадратного корня.
Цели урока:
Образовательные:
- Закрепить и систематизировать знания по теме «Свойства арифметического квадратного
корня».
- Сформировать умение применять их для преобразования выражений, содержащих
квадратные корни.
- Научиться вычислять значения квадратных корней.
Задачи:
Воспитательные:
- Воспитывать внимательность, аккуратность, настойчивость
Развивающие:
- развитие памяти
- развитие логического мышления
- аргументированной математической речи
Формы и методы работы
- фронтальный (устный счет)
- индивидуальная работа с дифференциацией(карточки)
- эвристический
Устно:
Ответьте на вопросы
Вопрос: Что называется арифметическим квадратным корнем?
Ответ: Арифметическим квадратным корнем называется неотрицательное число, квадрат
которого равен числу.
Вычислите
√81; √ 0,04; √ 81/4; √ 25/16; √ !600 ;
√ 0,49 + √ 0,16; √ -100; 1,2√ 49;
√ 36 √ 16 ; 3√9 - 16;
√0; √ -225; ( √ 0,4)²; ( √ 15 )²; ( -3 √6)².
Верны ли данные равенства? Почему?
1) 16  4
4)  9  3
2) 25  5
5) 9  3
3) 8  3
6) 64  4
Выберите верные равенства. Тест (Цоры)
Вопрос?
Какие свойства арифметического квадратного корня вы знаете?
Ответ:
1.Корень из произведения неотрицательных множителей равен произведению корней из
этих множителей:
ав  а в , а  0, в  0
2.Корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен
корню из числителя, деленному на корень из знаменателя.
а:в 
а
в
а  0, в  0
,
Тождества
удобно использовать, поменяв их части местами:
ав  а в , а  0, в  0 ,
а:в 
а
в
,
а  0, в  0
Тест.(32 тест 8)(цоры)
Вычислите:
Задание 1. Вычислите значения корня
Задание 2. Найти значения выражения
Задание 3.Вычислить значения корня
Задание 4. Найти значения выражения
Задание 5. Найти значения выражения
Разминка. Она у нас не совсем обычная.
Все любят разгадывать кроссворд, а мы займемся разгадыванием кросснамбера:
КРОССНАМБЕР- игра-задача, в которой фигура из рядов пустых клеток заполняется
перекрещивающимися числами с буквами, заданными по условиям игры.
• Разгадать кросснамбер
По горизонтали:
• Б) 11²+10√(-3)²=
• Г) 17²=
• Д) 10√361=
• Е) 6,63·10²=
По вертикали:
• А) √225=
• Б) 14=√ ?
• В) 10²+√169
• Ж) (√64)²
Разминка прошла удачно!
Работаем по учебнику:
Решить №361(а,в), 372(в,г), №358(в,д), 373(а,б)
Физкультминутка.(музыка)
Вы на славу потрудились,
И немного утомились,
Дружно стать нам всем пора:
Начинается зарядка!
Вопрос: Чему равен квадратный корень из степени?
Ответ.
Вопрос: Как извлечь корень из степени с четным показателем?
Ответ.
Чтобы извлечь корень из степени с четным показателем, надо представить подкоренное
выражение в виде квадрата некоторого выражения и использовать рассмотренное
тождество:
х2  х
Пример: √ (1,7)²=1,7;
√ (-19)²=19;
√ а²=|а|=а, если а≥0 ;
√ в²=|в|= -в , если в<0
Тест(33)
Творческие задания:
1.Найти значения выражения
2.Упростите выражения:
3.Вычислите:
4.Решите уравнения:
Самопроверка: ( на каждой парте лежат листочки с заданиями по вариантам)
Выполните их
Проверить ответы: ответы на компьютере:
•
•
•
•
•
•
•
1 вариант
а) 2/7
б) 3/8
б) 3/4
в) 8/9
г) 4/3
д) 3/2
•
•
•
•
•
•
3 вариант
а) 2/3
б) 3/4
в) 8/9
г) 4/3
д) 3/2
2 вариант
а) 3/7
б) 5/9
б) 2/5
в) 3/10
г) 1/9
д) 10/9
4 вариант
а) 5/7
б) 2/5
в) 3/10
г) 1/9
д) 10/9
Домашнее задание: карточки по вариантам
Итог урока:
- Как найти корень из произведения?
- Как найти корень из дроби?
- Может ли в знаменателе быть ноль?
- Как найти корень из смешанной дроби?
К математике способность проявляйте,
Не ленитесь, а ежедневно развивайтесь.
Умножайте, делите, трудитесь, соображайте,
С математикой дружить не забывайте.
- Урок окончен. Спасибо. До свидания.