МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра функционального анализа и аналитической экономики
Кравченко
Полина Геннадьевна
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН
Дипломная работа
Научный руководитель:
канд. физ.-мат. наук,
доцент С. П. Сташуленок
Допущена к защите
«___» ____________ 2019 г.
Зав. кафедрой функционального анализа и аналитической экономики
доктор физ.-мат. наук, профессор А. В. Лебедев
Минск, 2019
ОГЛАВЛЕНИЕ
РЕФЕРАТ ..................................................................................................................... 3
РЭФЕРАТ ..................................................................................................................... 4
ABSTRACT .................................................................................................................. 5
ВВЕДЕНИЕ .................................................................................................................. 6
ГЛАВА 1....................................................................................................................... 7
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ ................................................................... 7
ГЛАВА 2..................................................................................................................... 21
ПРОВЕРКИ ГИПОТЕЗ О ВИДЕ РАСПРЕДЕЛЕНИЯ .......................................... 21
ГЛАВА 3..................................................................................................................... 35
ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ...........................................................
СЛУЧАЙНЫХ ВЕЛИЧИН ....................................................................................... 35
ЗАКЛЮЧЕНИЕ ......................................................................................................... 40
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ ................................................. 41
2
РЕФЕРАТ
В данной дипломной работе содержится
-
41 страниц,
-
14 рисунков,
-
8 литературных источников.
Ключевые слова: СЛУЧАЙНЫЕ ВЕЛИЧИНЫ, РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ
СЛУЧАЙНЫХ
СТАТИСТИЧЕСКИХ
ГИПОТЕЗ,
ВЕЛИЧИН,
МОДЕЛИРОВАНИЕ
ПРОВЕРКА
СЛУЧАЙНЫХ
ВЕЛИЧИН, УРОВЕНЬ ЗНАЧИМОСТИ.
Цель
дипломной
работы:
изучение
распределений
вероятностей
случайных величин, основных дискретных и абсолютно непрерывных
распределений случайных величин, связей между случайными величинами,
проверка гипотез о виде распределения.
3
РЭФЕРАТ
У дадзенай дыпломнай працы ўтрымліваецца
-
41 старонак,
-
14 малюнкаў,
-
8 літаратурных крыніц.
Ключавыя словы: ВЫПАДКОВЫЯ ВЕЛІЧЫНІ, РАЗМЕРКАВАННЯ
ВЕРАГОДНАСЦЯЎ
ВЫПАДКОВАЙ
ВЕЛІЧЫНІ,
ПРАВЕРКА
СТАТЫСТЫЧНЫХ ГІПОТЭЗ, МАДЭЛЯВАННЕ ВЫПАДКОВАЙ ВЕЛІЧЫНІ,
УЗРОВЕНЬ ЗНАЧНАСЦІ.
Мэта дыпломнай працы: вывучэнне размеркаванняў верагоднасцяў
выпадковых велічынь, асноўных дыскрэтных і абсалютна бесперапынных
размеркаванняў выпадковых велічынь, сувязяў паміж выпадковымі велічынямі,
праверка гіпотэз аб выглядзе размеркавання.
4
ABSTRACT
Diploma thesis contains
-
41 pages,
-
14 figures,
-
8 references sources.
Key
words:
PROBABILITIES
OF
RANDOM
VALUES,
DISTRIBUTIONS
RANDOM
VALUES,
CHECK
OF
OF
THE
STATISTICAL
HYPOTHESES, MODELING RANDOM VALUES, SIGNIFICANCE LEVEL.
The aim of the diploma paper: the study of the probability distributions of
random variables, the main discrete and absolutely continuous distributions of
random variables, connection between random variables, testing hypotheses about the
type of distribution.
5
ВВЕДЕНИЕ
Теория вероятностей широко применяется в различных областях
человеческой жизни, как метод систематизации данных для выявления
закономерностей
природы,
человеческого
поведения,
экономических
параметров и др. Поэтому изучение вопросов распределения вероятностей
случайных величин является актуальным.
В связи с этим целью данной дипломной работы послужило изучение
распределения вероятностей случайных величин. В ходе выполнения работы
были
рассмотрены
основные
дискретные
и
абсолютно
непрерывные
распределения случайных величин. Были проверены гипотезы о виде
распределения и качества моделирования этих распределений с помощью
программы STATISTICA, а также были установлены взаимосвязи между
распределениями вероятностей случайных величин.
В первой главе приводятся теоретические сведения о случайных
величинах, а также представлены плотности и функции распределения для
основных распределений случайных величин.
Во второй главе описаны критерии проверки гипотез, а именно критерий
согласия Колмогорова, критерий согласия хи-квадрат для простой гипотезы и
критерий согласия хи-квадрат для сложной гипотезы. Была проведена проверка
гипотез о виде распределения используя программу STATISTICA.
В третьей главе были рассмотрены основные примеры внутренних
взаимосвязей между распределениями случайных величин.
6
ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Фундаментальным
понятием
любого
статистического
выражения
является случайная величина.
Для того, чтобы дать определение случайной величины, сначала
необходимо задать вероятностное пространство (, A, Р), где – множество
элементарных событий, A – сигма-алгебра событий, Р – вероятность. Тогда
случайной величиной можно считать функцию , действующую из в R такую,
что для любого cR выполняется следующее условие {: ()c} A.
Для понимания случайной величины введем еще одно определение:
случайной величиной называется функция , которая действует из в R такая,
что для любого борелевского множества BB(R) −1 (B) A. Здесь −1 (B)=
{: ()B}.
Задать
случайную
величину
означает
задать
ее
распределение
вероятностей.
Под
распределением
вероятностей
понимают
функцию,
описывающую вероятность получения возможных значений, которые может
принимать случайная величина т.е. функция 𝑃𝜉 : B(R)[0,1] такая, что для
любого BB(R) 𝑃𝜉 (B)=P(B).
Распределение вероятностей 𝑃𝜉 однозначно определяется функцией
распределения 𝐹𝜉 . Под функцией распределения случайной величины
понимают такую функцию 𝐹𝜉 , которая действует из R в отрезок [0,1], что для
любых xR: 𝐹𝜉 (x)=P{: ()x}.
Утверждение:
Для любого BB(R) выполняется следующее равенство:
𝑃𝜉 (B)=∫𝐵 𝑑 𝐹𝜉 (𝑥),
7
(1)
где 𝑥 ∈ 𝑅, 𝐹𝜉 (𝑥) функция распределения случайной величины.
Докажем, что любое числовое множество, составленное из конечных
сумм непересекающихся полуинтервалов (𝑥1 , 𝑥2 ]={ 𝑥 R: 𝑥1, 𝑥 𝑥2 }, образует
алгебру B 0 , которая в последствии образует сигма-алгебру борелевских
множеств B. По определению класс подмножеств B0 пространства (в данном
случае в качестве выступает числовая ось) является алгеброй если
выполняются следующие условия:
1)
и лежат в B 0 ,
2)
B 0 замкнуто относительно пересечения двух множеств,
3)
дополнение B 0 также лежит в B 0 .
Добавим в B 0 и R, таким образом выполняется первый пункт
определения. B 0 будет замкнуто относительно операции пересечения так как
пересечением двух полуинтервалов будет либо конечное объединение
непересекающихся полуинтервалов, либо пустое множество. Дополнение
B 0 будет также лежать в B 0 так как R\((𝑥𝑖 , 𝑥𝑗 ]) равно ( R\(𝑥𝑖 , 𝑥𝑗 ]), что
принадлежит B 0 . В результате мы доказали, что B 0 является алгеброй, очевидно
не будет являться сигма-алгеброй.
Рассмотрим событие, которое заключается в том, что попала в какое-то
объединение промежутков.
𝑃( ∈∪ (𝑥𝑖 , 𝑥𝑗 ]) = 𝑃 (∪ ( ∈ (𝑥𝑖 , 𝑥𝑗 ])),
что является свойством полного прообраза.
Вероятность объединения будет равна сумме вероятностей, так как
интервалы непересекающиеся, из чего следует, что события несовместны, то
есть
𝑃(∪ ( ∈ (𝑥𝑖 , 𝑥𝑗 ]))=𝑃( ∈ (𝑥𝑖 , 𝑥𝑗 ])=∫(𝑥 ,𝑥 ] 𝑑 𝐹𝜉 = ∫(𝑥 ,𝑥 ] 𝑑 𝐹𝜉 .
𝑖
8
𝑗
𝑖
𝑗
Последнее равенство выполняется так как интеграл обладает свойством
сигма-аддитивности по множеству.
Таким образом, раз данное равенство верно для объединения любых
непересекающихся полуинтервалов, то оно будет верно и для любых элементов
алгебры.
Далее по теореме Каратеодори можем продолжить распределение
вероятностей на сигма-алгебру.
Теорема Каратеодори.
Если на алгебре B 0 подмножеств определена вероятность P, такая что
аксиома счетной аддитивности формулируется следующим образом: если
∞
попарно несовместные 𝐵𝑛 B 0 и B=∑∞
𝑛=1 𝐵𝑛 B 0 , то P(B)= ∑𝑛=1 P(𝐵𝑛 ), то эту
вероятность можно однозначно продолжить на все множества из сигма-алгебры
B, порождённой B 0 .
Из единственности продолжения следует, что равенство (1) верно и для
сигма-алгебр.⊠
Далее можно классифицировать случайные величины на основе их
вероятностного распределения. Если вероятности 𝑃{𝜉 = 𝑥𝑘 } = 𝑝𝑘 так, что
∑∞
𝑘=1 𝑝𝑘 = 1, то случайная величина имеет дискретное распределение.
Примерами дискретных распределений являются:
1)
Биномиальное
𝑃{𝜉 = 𝑘} = 𝐶𝑛𝑘 𝑝𝑘 (1 − 𝑝)𝑛−𝑘 , k = 0,1,…,n; 0 < p < 1.
2)
Пуассоновское
𝑃{𝜉 = 𝑘} =
3)
𝑎𝑘
𝑘!
𝑒 −𝑎 , k = 0,1,…,n; 0 < a.
Геометрическое
𝑃{𝜉 = 𝑘} = 𝑝(1 − 𝑝)𝑘 k = 0,1,…,n; 0 < p < 1.
9
Если случайная величина имеет плотность распределения, то есть такую
функцию 𝑝(𝑥) = 𝑝𝜉 (𝑥), что для любых 𝑥1 < 𝑥2
выполняется следующее
равенство:
𝑥2
𝑃{𝑥1 < 𝜉 < 𝑥2 } = ∫ 𝑝𝜉 (𝑥)𝑑𝑥.
𝑥1
В этом случае говорят, что случайная величина имеет абсолютно
непрерывное
распределение.
Примеры
абсолютно
непрерывных
распределений случайных величин:
1) Нормальная случайная величина (случайная величина Гаусса).
Случайная величина имеет нормальное распределение (распределение Гаусса)
с параметрами 𝜇 и 𝜎 2, если ее плотность распределения имеет вид:
𝑝𝜉 (𝑥) =
1
𝜎√2𝜋
(𝑥−𝜇)2
−
𝑒 2𝜎2 ,
𝜎 > 0,
𝜇 ∈ 𝑅.
Функция распределения нормальной случайной величины задается
следующим образом:
𝐹𝜉 (𝑥) =
1
𝜎√2𝜋
𝑥
∫
(𝑥−𝜇)2
−
𝑒 2𝜎2
𝑑𝑥.
−∞
Если 𝜇 = 0, 𝜎 = 1, то данное распределение называется стандартным
нормальным распределением.
График плотности вероятности нормального распределения преставлен
на рис.1.
10
Рис. 1 График плотности вероятности нормального распределения
2)
Экспоненциальная (показательная) случайная величина. Случайная
величина обладает экспоненциальным (показательным) распределением с
параметром ( > 0), если ее плотность имеет вид
0,
𝑝𝜉 (𝑥) = { −𝜆𝑥
𝜆𝑒 ,
𝑥 < 0,
𝑥 ≥ 0.
Функция распределения случайной величины, которая подчиняется
экспоненциальному закону выглядит следующим образом:
0,
𝐹𝜉 (𝑥) = {
1 − 𝑒 −𝜆𝑥 ,
3)
Равномерная
на
𝑥 < 0,
𝑥 ≥ 0.
случайная
[𝑎; 𝑏]
величина.
Равномерно
распределенная на отрезке [𝑎; 𝑏] случайная величина имеет плотность
распределения:
11
0,
𝑥 ∉ [𝑎; 𝑏],
𝑝𝜉 (𝑥) = { 1
,
𝑏−𝑎
𝑥 ∈ [𝑎; 𝑏].
Для случайной величины равномерно распределенной на [𝑎; 𝑏] функция
распределения представляется в следующем виде:
0,
𝑥−𝑎
,
𝐹𝜉 (𝑥) = {
𝑏−𝑎
1,
4)
Случайная
величина
Коши.
𝑥 < 𝑎,
𝑎 ≤ 𝑥 < 𝑏,
𝑥 ≥ 𝑏.
Случайная
величина
имеет
распределение Коши, если ее плотность представима в виде
𝑝𝜉 (𝑥) =
1
с
∙ 2
,
𝜋 𝑥 + 𝑐2
𝑐 > 0,
𝑥 ∈ 𝑅.
Функция распределения Коши имеет вид:
𝐹𝜉 (𝑥) =
1
𝑥
1
𝑎𝑟𝑐𝑡𝑔 ( ) +
𝜋
𝑐
2
График плотности вероятности рапределения Коши представлен на рис. 2.
12
Рис. 2 График плотности вероятности распределения Коши
5)
Случайная величина Лапласа. Случайная величина имеет
распределение Лапласа, если ее плотность представима в виде
𝜆
𝑝𝜉 (𝑥) = 𝑒 −𝜆|𝑥−𝑎| ,
2
𝜆 > 0,
𝑎 ∈ 𝑅,
𝑥 ∈ 𝑅.
Функция распределения случайной величины Лапласа задается следующим
образом:
1 𝛼(𝑥−𝛽)
𝑒
,
2
(𝑥)
𝐹𝜉
={
1
1 − 𝑒 −𝛼(𝑥−𝛽) ,
2
6) Логнормальное
распределение.
Пусть
𝑥 ≤ 𝛽,
𝑥 > 𝛽.
распределение
величины задается плотностью вероятностей:
𝑝𝜉 (𝑥) =
1
𝑥𝜎√2𝜋
13
(ln 𝑥−𝜇)2
−
2𝜎 2 ,
𝑒
случайной
где 𝑥 > 0, 𝜎 > 0, 𝜇 ∈ 𝑅. Тогда говорят, что случайная величина имеет
логнормальное распределение с параметрами 𝜇 и 𝜎.
Формула для функции распределение логнормального закона имеет вид:
𝐹𝜉 (𝑥) = Ф (
ln 𝑥
),
𝜎
𝑥 ≥ 0, 𝜎 > 0,
где Ф функция распределения нормального закона.
7)
Бета-распределение.
Случайная
величина
имеет
бета-
распределение, если ее плотность задается в следующем виде:
1
𝑥 𝛼−1 (1 − 𝑥)𝛽−1 ,
𝑝 (𝑥) = {𝐵(𝛼, 𝛽)
0,
0 ≤ 𝑥 ≤ 1, 𝛼, 𝛽 > 0,
𝑥 ∉ [0,1],
1
где 𝐵(𝛼, 𝛽) = ∫0 𝑥 𝛼−1 (1 − 𝑥)𝛽−1 𝑑𝑥 бета-функция.
Для случайной величины, подчиняющейся бета-распределению, функция
распределения имеет вид:
0,
𝐹𝜉 (𝑥) =
𝑥 < 0,
𝑥
∫0 𝑡 𝛼−1 (1 − 𝑡)𝛽−1 𝑑𝑡
,
1
∫0 𝑡 𝛼−1 (1 − 𝑡)𝛽−1 𝑑𝑡
{
1,
0 ≤ 𝑥 ≤ 1,
𝑥 > 1.
Например, бета-распределение с параметрами 𝛼 = 1 и 𝛽 = 1 является
равномерно распределенной случайной величиной на отрезке [0;1].
8)
Распределение 𝜒 2 . Пусть случайные величины 𝜉1 , … , 𝜉𝑛 , независимы
и имеют стандартное нормальное распределение, тогда можно образовать
случайную величину 𝜒𝑛2 = 𝜉12 + ⋯ + 𝜉𝑛2 . Распределение вероятностей случайной
величины 𝜒𝑛2 , определенной таким образом, называется 𝜒 2 – распределением с n
14
степенями свободы. Выражение для плотности которой выглядит следующим
образом:
𝑛
𝑥
𝑥 2 −1 𝑒 −2
,
𝑝(𝑛) (𝑥) = Г(1 𝑛)2𝑛2
2
{ 0,
𝑥 ≥ 0,
𝑥 < 0,
∞
где Г(𝑧) гамма-функция, Г(𝑧) = ∫0 𝑡 𝑧−1 𝑒 −𝑡 𝑑𝑡, 𝑧 ∈ ℂ.
График плотности вероятности распределения 𝜒 2 представлен на рис. 3.
Рис. 3 График плотности вероятности распределения 𝜒 2
Обозначим через 𝐹 (𝑛) (𝑥) функцию распределения случайной величины
𝜒𝑛2 . Тогда для x < 0 получаем 0, а для x 0:
𝑛
𝑡
𝑡 2 −1 𝑒 −2
(𝑛)
𝐹 (𝑥) = ∫
𝑛 𝑑𝑡 .
1
0 Г ( 𝑛) 2 2
2
𝑥
15
9)
Гамма-распределение. Если распределение случайной величины
задается плотностью вероятностей, имеющей вид:
𝑥
𝑒 −𝜃
𝑘−1
,
𝑝 (𝑥) = {𝑥
𝜃𝑘 Г(𝑘)
0,
𝑥≥0
𝑥<0
где Г(𝑘) – гамма-функция. Тогда случайная величина имеет гаммараспределение с параметрами и k. Более того существует связь между гаммараспределением и экспоненциальным, а также между гамма-распределением и
распределением 𝜒 2 . То есть гамма-распределение является частным случаем
1
экспоненциального: Г (1, ) ≡ exp(𝜆). И гамма-распределение является частным
𝜆
𝑛
случаем распределения 𝜒 2 : Г ( , 2) ≡ 𝜒 2 (𝑛).
2
Так как функция гамма-распределения через элементарные функции не
выражается, то ее можно представить только в следующем виде:
𝑥
𝑒 −𝜃
𝑘−1
𝑑𝑥,
𝐹𝜉 (𝑥) = ∫ 𝑝 (𝑥)𝑑𝑥 = {∫ 𝑥
𝜃𝑘 Г(𝑘)
−∞
−∞
0,
𝑥
𝑥
𝑥 ≥ 0,
𝑥 < 0.
10) Распределение Фишера. Если 𝜂1 и 𝜂2 независимые случайные
величины, которые имеют распределение 𝜒 2 с 𝑑1 и 𝑑2 степенями свободы
соответственно,
то
распределение
случайной
величины
𝐹𝑑1 ,𝑑2 =
𝜂1 /𝑑1
𝜂2 /𝑑2
называется распределением Фишера с параметрами 𝑑1 и 𝑑2 . Плотность данного
распределения имеет вид:
𝑑 + 𝑑2 𝑑1 𝑑1 /2
𝑑1
Г( 1
)( )
𝑥 2 −1
2
𝑑2
𝑝(𝑥) =
, 𝑥 ≥ 0.
𝑑1
𝑑2
𝑑1
(𝑑
+𝑑
)/2
1
2
Г( )Г( )
[( ) 𝑥 + 1]
2
2
𝑑2
16
График плотности вероятности плотности распределения Фишера
представлен на рис. 4.
Рис. 4 График плотности вероятности распределения Фишера
Функция распределения Фишера 𝐹𝜉 (𝑥) вычисляется по формуле
𝐹𝜉 (𝑥) = 0,
𝑥 ≤0
а при 𝑥 > 0
∞
𝑣𝑥
1
𝑑
−1
−𝑣
𝐹𝜉 (𝑥) =
∫ 𝑣 2 𝑒 (∫ 𝑢𝑑1−1 𝑒 −𝑢 𝑑𝑢)𝑑𝑣
Г(𝑑1 )Г(𝑑2 ) 0
0
11)
Распределение Стьюдента. Пусть 𝜉0 , 𝜉1 , … , 𝜉𝑛 независимы и имеют
стандартное нормальное распределение, тогда распределение случайной
величины 𝑡𝑘
𝜉0
1
𝑘
√ (𝜉12 +⋯+𝜉𝑘2 )
=
𝜉0
2
√𝜒𝑘
называют распределением Стьюдента с k
𝑘
степенями свободы. Плотность распределения Стьюдента с k степенями свободы
равна:
17
−(𝑘+1)/2
𝑥2
𝑝𝑘 (𝑥) =
(1 + )
𝑘
√𝜋𝑘Г(𝑘/2)
Г((𝑘 + 1)/2)
График плотности вероятности распределения Стьюдента представлен на
рис. 5.
Рис. 5 График плотности вероятности распределения Стьюдента
Распределение Стьюдента симметричное
𝐹𝑡𝑘 (𝑥) = 𝐹−𝑡𝑘 (𝑥).
Поскольку случайная величина −𝜉0 имеет, как и случайная величина 𝜉0 ,
стандартное нормальное распределение.
12) Распределение
Колмогорова.
Случайная
величина
имеет
распределение Колмогорова, если ее функция распределения имеет следующий
вид:
18
∞
𝐹 (𝑥) = {
∑ (−1)𝑘 𝑒 −2𝑘
2𝑥2
,
𝑥>0
𝑘=−∞
0,
𝑥 ≤ 0.
Определение.
Если функция распределения случайной величины является непрерывной
функцией, у которой множество точек роста имеет нулевую меру Лебега, то
говорят, что случайная величина имеет сингулярное распределение.
Примером такой функции служит канторова функция 𝐹(𝑥), которую
можно определить следующими равенствами 𝐹(𝑥) = 0 при 𝑥 ≤ 0, 𝐹(𝑥) =
1 при 𝑥 ≥ 1 и
𝐹(𝑥) =
{
1
1
𝐹(3𝑥)
при 0 ≤ 𝑥 ≤ ,
2
3
1
1
2
при ≤ 𝑥 ≤ ,
2
3
3
1 1
2
+ 𝐹(3𝑥 − 2) при ≤ 𝑥 ≤ 1.
2 2
3
Таким образом, множество случайных величин можно разделим на 3
класса: дискретные, абсолютно непрерывные и сингулярные случайные
величины. И эта классификация является полной, что можно подтвердить
следующей теоремой.
Теорема.
Любая функция распределения 𝐹(𝑥), 𝑥 ∈ 𝑅, единственным образом
представима в виде:
𝐹(𝑥) = 𝑎1 𝐹1 (𝑥) + 𝑎2 𝐹2 (𝑥) + 𝑎3 𝐹3 (𝑥),
19
где 𝐹1 (𝑥) – дискретная функция распределения, 𝐹2 (𝑥) – абсолютно непрерывная
функция распределения, 𝐹3 (𝑥) – сингулярная функция распределения, 𝑎𝑖 ≥
0 и 𝑎1 + 𝑎2 + 𝑎3 =1.
20
ГЛАВА 2
ПРОВЕРКИ ГИПОТЕЗ О ВИДЕ РАСПРЕДЕЛЕНИЯ
Одной из основных задач математической статистики является
разработка
рациональных
методов
проверки
статистических
гипотез.
Статистическая гипотеза – это любое утверждение, касающееся параметров или
распределения вероятностей наблюдаемых в эксперименте случайных величин.
Рассмотрим основные критерии согласия проверки гипотез.
Критерий согласия Колмогорова.
Критерий Колмогорова применяют в тех случаях, когда функция
распределения непрерывна.
Пусть 𝑋 = (𝑋1 , … , 𝑋𝑛 ) – выборка из распределения ℒ(𝜉) с неизвестной
функцией распределения 𝐹 (𝑥), о которой выдвинута простая гипотеза
𝐻0 : 𝐹𝜉 (𝑥) = 𝐹(𝑋). Статистикой критерия является величина
𝐷𝑛 = 𝐷𝑛 (𝑥) = 𝑠𝑢𝑝−∞<𝑥<∞ |𝐹𝑛 (𝑥) − 𝐹 (𝑥)|,
представляющая собой максимальное отклонение эмпирической функции
распределения 𝐹𝑛 (𝑥) от гипотетической функции распределения 𝐹(𝑥). При
каждом x величина 𝐹𝑛 (𝑥) является оптимальной оценкой для 𝐹(𝑥) и с
увеличением объема выборки n происходит сближение 𝐹𝑛 (𝑥) с 𝐹(𝑥), поэтому, по
крайней мере при больших n, в тех случаях, когда гипотеза 𝐻0 истинна, значение
𝐷𝑛 не должно существенно отклоняться от нуля. Отсюда следует, что
критическую область критерия, основанного на статистике 𝐷𝑛 , следует задавать
в виде 𝐹1𝛼 = {𝑡 ≥ 𝑡𝛼 }.
Особенностью статистики 𝐷𝑛 является то, что ее распределение при
гипотезе 𝐻0 не зависит от вида функции 𝐹(𝑥).
21
Вторым замечательным фактом является то, что распределение
статистики 𝐷𝑛 при достаточно больших n (уже при 𝑛 ≥ 20) практически от n не
зависит и имеет следующий вид:
∞
lim 𝑃(√𝑛 𝐷𝑛 ≤ 𝑡) = 𝐾(𝑡) = ∑ (−1)𝑘 𝑒 −2𝑘
𝑛→∞
2𝑡 2
.
𝑘=−∞
В итоге правило проверки гипотезы 𝐻0 выглядит следующим образом:
если
наблюдавшееся
значение
𝑡 = 𝐷𝑛 (𝑥)
статистики
𝐷𝑛 = 𝐷𝑛 (𝑥) =
𝑠𝑢𝑝−∞<𝑥<∞ |𝐹𝑛 (𝑥) − 𝐹 (𝑥)| удовлетворяет неравенству √𝑛𝑡 ≥ 𝜆𝛼 , где 𝐾(𝜆𝛼 ) =
1 − 𝛼, то гипотезу 𝐻0 отвергают; в противном случае делают вывод, что
статистические данные не противоречат гипотезе. Следуя этому правилу, можно
ошибочно отклонить гипотезу 𝐻0 , когда она верна, с вероятностью,
приблизительно равной .
Критерий согласия 𝝌𝟐 К. Пирсона.
Предположим 𝑋 = (𝑋1 , … , 𝑋𝑛 ) это выборка из распределения ℒ(𝜉) с
неизвестной функцией распределения 𝐹𝜉 (𝑥), о которой выдвинута простая
гипотеза 𝐻0 : 𝐹𝜉 (𝑥) = 𝐹(𝑥). Одним из наиболее известных критериев проверки
этой гипотезы является критерий 𝜒 2 .
Он применяется для любых распределений, для многомерных в том
числе. Для того, чтобы воспользоваться этим критерием, выборочные данные
предварительно группируются в следующем виде.
Предположим 𝜈 = (𝜈1 , … , 𝜈𝑁 ) – вектор частот попадания выборочных
точек в соответствующие интервалы группировки 𝜀1 , … , 𝜀𝑁 (𝜈1 +. . + 𝜈𝑁 = 𝑛) и
𝑝0 = (𝑝10 , … , 𝑝𝑁0 ), где 𝑝𝑗0 = 𝑃(𝜉 ∈ 𝜀𝑗 |𝐻0 ), 𝑗 = 1, … , 𝑁. Тогда ℒ(𝜈|𝐻0 ) = 𝑀(𝑛; 𝑝0 ) и
гипотеза 𝐻0 сводится к гипотезе о том, что вероятности полиномиального
распределения построенного вектора частот 𝜈 имеют заданные значения 𝑝𝑗0 𝑗 =
1, … , 𝑁. В качестве статистики, которая характеризует отклонение выборочных
22
данных (т.е. частот 𝜈𝑗 ) от соответствующих гипотетических значений (в данном
случае от средних 𝐸(𝜈𝑗 |𝐻0 ) = 𝑛𝑝𝑗0 ), принимают величину
𝜒𝑛2
=
𝜒𝑛2 (𝜈)
=
0 2
𝑁 (𝜈𝑗 −𝑛𝑝𝑗 )
∑𝑗=1
𝑛𝑝0
𝑗
= ∑𝑁
𝑖=1
𝜈𝑖 2
𝑛𝑝𝑗0
− 𝑛,
а критическую область задают в виде ℱ1𝑎 = {𝑡 ≥ 𝑡𝑎 }. Точное распределение
ℒ(𝜒𝑛2 |𝐻0 ) неудобно для вычисления критической границы 𝑡𝑎 , но при этом для
больших объемов выборок 𝑛 статистика 𝜒𝑛2 имеет при гипотезе 𝐻0 простое
предельное распределение, которое не зависит от гипотезы(т.е. от чисел 𝑝𝑗0 ).
Теорема.
Если 0 < 𝑝𝑗0 < 1, 𝑗 = 1, … , 𝑁, то при 𝑛 → ∞ ℒ(𝜒𝑛2 |𝐻0 ) → 𝜒 2 (𝑁 − 1)
Подводя итог, критерий согласия 𝜒 2 имеет следующий вид:
предположим заданы уровень значимости и объем выборки n и
наблюдавшиеся значения ℎ = (ℎ1 , … , ℎ𝑁 ) вектора частот ν = (ν1 , … , νN )
удовлетворяют
условиям
наблюдавшееся
∑𝑁
𝑗=1
(𝜈𝑗 −𝑛𝑝𝑗0 )2
𝑛𝑝𝑗0
= ∑𝑁
𝑖=1
значение
𝜈𝑖 2
𝑛𝑝𝑗0
𝑛 ≥ 50, ℎ𝑗 ≥ 5, 𝑗 = 1, … , 𝑁;
𝑡 = 𝜒𝑛2 (ℎ)
статистики
тогда,
если
𝜒𝑛2 = 𝜒𝑛2 (𝜈) =
2
− 𝑛 удовлетворяет неравенству 𝑡 ≥ 𝜒1−𝑎,𝑁−1
, то
гипотеза 𝐻0 отвергается; иначе гипотеза 𝐻0 не противоречит результатам
испытаний.
Следует сделать пару общих замечаний. Критерий согласия 𝜒 2
применяется в тех случаях, когда в каждом опыте наблюдается одно из 𝑁
несовместных событий 𝐴1 , … , 𝐴𝑁 и заданы частоты появлений этих событий в 𝑛
испытаниях. В случае, если выборка имеет непрерывный закон распределения,
то, используя предварительно метод группировки данных, рассматривают
дискретную схему, в которой в качестве события 𝐴𝑖 рассматриваются события
{𝜉 ∈ 𝜀𝑖 }, где 𝜀1 , … , 𝜀𝑁 – интервалы группировки. Недостатком метода является
потеря информации, которая происходит при группировке данных по
классам(интервалам). Вдобавок, остается еще вопрос о выборе числа интервалов
23
𝑁 и длине самих интервалов 𝜀𝑖 . Однако имеются и некоторые достоинства: при
применении критерия 𝜒 2 нет необходимости учитывать точные значения
наблюдений. Несомненными преимуществами критерия являются его простота,
наглядность и универсальность.
Критерий согласия 𝝌𝟐 для сложной гипотезы.
Описанный выше метод группировки наблюдений с последующим
применением критерия согласия 𝜒 2 применяется и в более сложной ситуации,
когда требуется проверить гипотезу о принадлежности неизвестной функции
распределения наблюдаемой в опыте случайной величины ξ заданному
семейству функций распределения. В общем виде задача формулируется
следующим образом. Пусть ℱ = {𝐹(𝑥; 𝜃), 𝜃 ∈ 𝛩} – заданное параметрическое
семейство функций распределения и 𝑋 = (𝑋1 , … , 𝑋𝑛 ) является выборок из
распределения ℒ(𝜉) с неизвестной функцией распределения. Задача состоит в
том, чтобы проверить гипотезу 𝐻0 : ℒ(𝜉) ∈ ℱ. Итак, в данном случае речь идет о
проверке сложной гипотезы.
Пусть
исходные
статистические
данные
сгруппированы
и
𝜈=
(𝜈1 , … , 𝜈𝑁 ) – соответствующий вектор частот попадания наблюдений в
интервалы группировки 𝜀1 , 𝜀2 , … , 𝜀𝑁 . Попытаемся составить статистику,
аналогичную
𝜒𝑛2 = 𝜒𝑛2 (𝜈) = ∑𝑁
𝑗=1
(𝜈𝑗 −𝑛𝑝𝑗0 )2
𝑛𝑝𝑗0
= ∑𝑁
𝑖=1
𝜈𝑖 2
𝑛𝑝𝑗0
− 𝑛. В этом случае
вероятности попадание в интервалы группировки при гипотезе 𝐻0 уже не будут
заданы однозначно, а являются некоторыми функциями от параметра 𝜃:
𝑝𝑖 (𝜃) = 𝑃(𝜉 ∈ 𝜀𝑖 |𝐻0 ) = ∫ 𝑑𝐹(𝑥; 𝜃), 𝑖 = 1, … , 𝑁.
𝜀𝑖
Поэтому статистика 𝜒𝑛2 принимает вид
𝜒𝑛2 = 𝜒𝑛2 (𝜃) = ∑𝑁
𝑖=1
(𝜈𝑖 −𝑛𝑝𝑖 (𝜃))2
𝑛𝑝𝑖 (𝜃)
24
Эта статистика зависит от неизвестного параметра; следовательно,
непосредственно использовать её для построения критерия пока нельзя,
требуется
предварительно
исключить
в
вышеуказанной
формуле
неопределенность, которая связана с неизвестным параметром 𝜃. Для этого
заменяют 𝜃 некоторой оценкой 𝜃̃𝑛 = 𝜃̃𝑛 (𝑋) и получают, таким образом,
статистику
𝜒̃𝑛2 = 𝜒̃𝑛2 (𝜃̃𝑛 ) = ∑𝑁
𝑖=1
̃𝑛 ))2
(𝜈𝑖 −𝑛𝑝𝑖 (𝜃
.
̃𝑛 )
𝑛𝑝𝑖 (𝜃
Эта статистика уже представляет собой функцию только от выборочных
данных; следовательно, её значение может быть однозначно вычислено для
каждой заданной реализации выборки 𝑋.
Если бы распределение статистики 𝜒̃𝑛2 при гипотезе 𝐻0 можно было найти
и при этом распределение не зависело бы от конкретных функций 𝐹(𝑥; 𝜃),
составляющих гипотезу 𝐻0 , то, основываясь на 𝜒̃𝑛2 , можно было бы построить
критерий согласия для гипотезы 𝐻0 .
В этом случае величины
𝑝𝑖 (𝜃̃𝑛 ) уже не являются постоянными, а
представляют собой функции от выборки (случайные величины). Поэтому
вышеупомянутая теорема к статистике 𝜒̃𝑛2 неприменима. Кроме того, следует
ожидать, что распределение этой статистики будет зависеть от способа
построения оценки 𝜃̃𝑛 . Существуют методы оценивания параметра 𝜃, при
которых предельное распределение имеет простой вид, а именно является
распределением хи-квадрат с числом степеней свободы 𝑁 − 1 − 𝑟, где 𝑟 –
размерность оцениваемого параметра 𝜃. Одним из таких методов оценивания
является метод максимального правдоподобия, основанный на частотах
𝜈1 , … , 𝜈𝑁 , т.е. когда в качестве 𝜃̃𝑛 в последней формуле используют
мультиномиальную оценку максимального правдоподобия.
25
Теорема.
Пусть
функция
𝑝𝑖 (𝜃), 𝑖 = 1, … , 𝑁, 𝜃 = (𝜃1 , … , 𝜃𝑟 ), 𝑟 < 𝑁 − 1,
удовлетворяет следующим условиям:
а) ∑𝑁
𝑖=1 𝑝𝑖 (𝜃) = 1, ∀𝜃 ∈ 𝛩;
б) 𝑝𝑖 (𝜃) ≥ 𝑐 > 0, 𝑖 = 1, … , 𝑁, и существуют непрерывные производные
𝜕𝑝𝑖 (𝜃)
𝜕𝜃𝑘
и
𝜕2 𝑝𝑖 (𝜃)
𝜕𝜃𝑘 𝜕𝜃𝑙
, 𝑘, 𝑙 = 1, … , 𝑟;
𝜕𝑝𝑖 (𝜃)
в) матрица (
Тогда если
𝜕𝜃𝑘
) размера 𝑁 × 𝑟 имеет ранг 𝑟 для всех 𝜃 ∈ 𝛩.
𝜃̃𝑛 = 𝜃̂𝑛 – мультиномиальная оценка максимального
правдоподобия для параметра 𝜃 и 𝜒̂ 𝑛2 = 𝜒𝑛2 (𝜃̂𝑛 ), то при 𝑛 → ∞ ℒ( 𝜒̂ 𝑛2 |𝐻0 ) →
𝜒 2 (𝑁 − 𝑟 − 1).
Далее описывается схема использования критерия согласия 𝜒 2 . Пусть в
опыте наблюдается одно из 𝑁 несовместных событий 𝐴1 , … , 𝐴𝑁 и о вероятностях
𝑝1 , … , 𝑝𝑁 появления этих событий выдвинута гипотеза
𝐻0 : 𝑝𝑖 = 𝑝𝑖 (𝜃), 𝑖 =
1, … , 𝑁, где 𝜃 = (𝜃1 , … , 𝜃𝑟 ) ∈ 𝛩 – некоторому невырожденному интервалу, и
функции 𝑝𝑖 (𝜃) удовлетворяют условиям теоремы (если в опыте наблюдается
случайная величина ξ непрерывного типа, то задачу сводят к такой дискретной
схеме, предварительно группируя данные по 𝑁 интервалам 𝜀1 , … , 𝜀𝑁 и
рассматривая в качестве 𝐴𝑖 события {𝜉 ∈ 𝜀𝑖 }). Допустим произведено 𝑛 ≥ 50
опытов и наблюдавшиеся частоты ℎ1 , … , ℎ𝑁 событий удовлетворяют условиям
ℎ𝑖 ≥ 5, 𝑖 = 1, … , 𝑁. Определим значение оценки 𝜃̂𝑛 , решая относительно 𝜃
уравнения ∑𝑁
𝑖=1
ℎ𝑖
𝜕𝑝𝑖 (𝜃)
𝑝𝑖 (𝜃) 𝜕𝜃𝑘
= 0, 𝑘 = 1, … , 𝑟.
Вычислим 𝑝𝑖 = 𝑝𝑖 (𝜃̂𝑛 ), 𝑖 = 1, … , 𝑁, и найдем значение статистики 𝜒̂ 𝑛2 по
формуле
𝑁
𝜒̂ 𝑛2
(ℎ𝑖 − 𝑛𝑝̂𝑖 )2
=∑
.
𝑛𝑝̂ 𝑖
𝑖=1
26
Если 𝜒̂ 𝑛2 ≥ 𝜒 2 (𝑁 − 𝑟 − 1), то гипотезу 𝐻0 следует отвергнуть; иначе
можно только сказать, что гипотеза 𝐻0 не противоречит результатам испытаний.
Согласно описанной теории, можно смело утверждать, что используя это
правило, можно ошибочно отклонить гипотезу 𝐻0 , когда она истинна, с
вероятностью, приближенно равной 𝑎.
В первой главе были приведены случайные величины. Смоделируем
некоторые из них и проверим качество моделирования с помощью критерия 𝜒 2
Пирсона в программе STATISTICA.
После генерации выборки, состоящей из 100 значений, следующим
шагом стала проверка ее распределения с помощью критерия 𝜒 2 .
1)
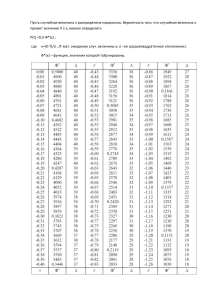
Гипотеза о нормальном распределении (рис. 6)
Рис. 6 – Изображение ожидаемого распределения первой выборки
Используя функцию RndNormal(x), где x дисперсия нормальной
случайной величины, сгенерируем выборку и проверим гипотезу о виде
распределения с помощью критерия согласия 𝜒 2 Пирсона. Используя
27
вероятностный калькулятор находим квантиль закона распределения. В силу
того, что квантиль закона распределения 𝜒 2 заданного уровня значимости 0.05
с 5 степенями свободы равен 11.070498, то есть больше полученной статистики
7.66344, то гипотеза о нормальном распределении выборки не отвергается.
Проверим действительно ли данная выборка распределена нормально.
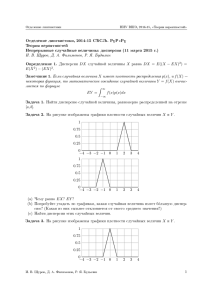
Предположим, что выборка подчиняется равномерному распределению (рис.7).
Рис. 7 – Изображение предполагаемого распределения первой выборки
Рассчитываем
в
вероятностном
калькуляторе
квантиль
закона
распределения. Видим, что квантиль закона распределения 𝜒 2 заданного уровня
значимости 0.05 с 7 степенями свободы равен 14.067140, что значительно
меньше, полученной статистики 48.3640. Таким образом, можно сделать вывод,
что данная выборка подчиняется нормальному распределению, а не
равномерному.
28
2)
Гипотеза о равномерном распределении (рис. 8)
Рис. 8 – Изображение ожидаемого распределения второй выборки
Применяя функцию Rnd(x), где x правая граница из интервала выборки,
образуем выборку, полученную случайным образом и докажем, что она имеет
равномерное распределение, используя критерий согласия 𝜒 2 Пирсона. С
помощью вероятностного калькулятора найдем квантиль закона распределения.
Так как квантиль закона распределения 𝜒 2 заданного уровня значимости 0.05 с
7 степенями свободы равен 14.067140, что больше данной статистики 6.68335,
то гипотеза о том, что данная выборка подчиняется равномерному
распределению принимается.
29
3)
Гипотеза о логнормальном распределении (рис. 9)
Рис. 9 – Изображение ожидаемого распределения третьей выборки
Воспользуемся функцией VLognorm(Rnd(x)), где x правая граница из
интервала выборки, для создания выборки далее покажем, что данная выборка
подчиняется
логнормальному
закону.
Рассчитываем
в
вероятностном
калькуляторе квантиль закона распределения. Видим, что квантиль закона
распределения 𝜒 2 заданного уровня значимости 0.05 с одной степенью свободы
равен 3.84159, что значительно больше, полученной статистики 0.76482. Таким
образом, можем принять гипотезу о логнормальном распределении данной
выборки.
30
4)
Гипотеза о гамма-распределении (рис. 10)
Рис. 10 – Изображение ожидаемого распределения четвертой выборки
Для создания выборки используем функцию VGamma(Rnd(x)), где x
правая граница из интервала выборки, и покажем, что данная выборка имеет
гамма-распределение. Применяя вероятностный калькулятор, рассчитаем
квантиль закона распределения. В связи с тем, что квантиль закона
распределения 𝜒 2 заданного уровня значимости 0.05 с 3 степенями свободы
равен 7.814728, что больше полученной статистики 1.71963, то гипотеза о гаммараспределении данной выборки не отвергается.
31
5)
Гипотеза о распределении Пуассона (рис. 11)
Рис. 11 – Изображение ожидаемого распределения пятой выборки
Сгенерируем выборку с помощью функции VPoisson(Rnd(x)), где x
правая граница из интервала выборки, и проверим гипотезу о виде
распределения с помощью критерия согласия 𝜒 2 Пирсона. Используя
вероятностный калькулятор, находим квантиль закона распределения. В силу
того, что квантиль закона распределения 𝜒 2 заданного уровня значимости 0.05
с 2 степенями свободы равен 5.991465, то есть больше полученной статистики
1.24292, то гипотеза о том, что выборка имеет распределение Пуассона не
отвергается.
32
6)
Гипотеза о распределении 𝜒 2 (рис .12)
Рис. 12 – Изображение ожидаемого распределения шестой выборки
Используя функцию VChi2(Rnd(x)), где x правая граница из интервала
выборки, создадим выборку и докажем, что данная выборка имеет
распределение 𝜒 2
используя критерий согласия 𝜒 2 Пирсона. С помощью
вероятностного калькулятора найдем квантиль закона распределения. Так как
квантиль закона распределения 𝜒 2 заданного уровня значимости 0.05 с 3
степенями свободы равен 7.814728, что больше данной статистики 5.12933, то
гипотеза о том, что данная выборка подчиняется распределению 𝜒 2
принимается.
33
7)
Гипотеза об экспоненциальном распределении (рис. 13)
Рис. 13 – Изображение ожидаемого распределения седьмой выборки
Применяя функцию VExpon(Rnd(x)), где x правая граница из интервала
выборки, сгенерируем выборку и покажем, что данная выборка подчиняется
экспоненциальному закону. Рассчитываем в вероятностном калькуляторе
квантиль закона распределения. Так как квантиль закона распределения 𝜒 2
заданного уровня значимости 0.05 с 7 степенями свободы равен 14.067140, что
значительно больше, полученной статистики 7.85132. Таким образом, можем
принять гипотезу об экспоненциальном распределении данной выборки.
34
ГЛАВА 3
ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ СЛУЧАЙНЫХ
ВЕЛИЧИН
Распределение вероятностей случайных величин обладает удивительным
количеством внутренних связей. В данной главе рассмотрим основные примеры
таких связей.
1)
Сумма двух случайных величин, подчиненных нормальным
законам.
В данном примере рассмотрим две случайные величины 𝑋 и 𝑌, которые
подчиняются нормальным законам, а также независимы.
Запишем плотности распределения каждой из случайных величин.
𝑝1 (𝑥) =
𝑝2 (𝑦) =
1
𝜎𝑥 √2𝜋
1
𝜎𝑦 √2𝜋
(𝑥−𝑎𝑥 )2
−
𝑒 2𝜎𝑥 2 ,
𝑒
(𝑦−𝑎𝑦 )2
−
2𝜎𝑦 2
.
Необходимо найти закон распределения следующей величины:
𝑍 = 𝑋 + 𝑌.
С этой целью воспользуемся формулой для композиции законов
распределения:
∞
𝑝(𝑧) = ∫ 𝑝1 (𝑥) 𝑝2 (𝑧 − 𝑥)𝑑𝑥 =
−∞
2
∞ −(𝑥−𝑎𝑥 )
1
2
=
∫ 𝑒 2𝜎𝑥
2𝜋𝜎𝑥 𝜎𝑦 −∞
35
(𝑧−𝑥−𝑎𝑦 )2
−
2𝜎𝑦 2
𝑑𝑥
Далее раскроем скобки в показателе степени подынтегральной функции,
приведем подобные и получим:
∞
1
2
𝑝(𝑧) =
∫ 𝑒 −𝐴𝑥 +2𝐵𝑥−𝐶 𝑑𝑥,
2𝜋𝜎𝑥 𝜎𝑦 −∞
где 𝐴 =
1 𝜎𝑥 2 +𝜎𝑦 2
2 𝜎𝑥 2 𝜎𝑦 2
, 𝐵=
𝑎𝑥
2𝜎𝑥
+
2
𝑧−𝑎𝑦
𝑎𝑥 2
(𝑧−𝑎𝑦 )2
2𝜎𝑦
2𝜎𝑥
2𝜎𝑥 2
, 𝐶=
2
+
2
.
После применим полученные выражения к интегралу Эйлера- Пуассона:
∞
∫ 𝑒
−𝐴𝑥 2 ±2𝐵𝑥−𝐶
−∞
𝜋 −𝐴𝐶−𝐵2
𝑑𝑥 = √ 𝑒 𝐴
𝐴
Затем подставляя данные выражения получим:
𝑝(𝑧) =
1
1
√𝜎𝑥 2 + 𝜎𝑦 2 √2𝜋
𝑒
[𝑧−(𝑎𝑥 +𝑎𝑦 )]2
−
2(𝜎𝑥 2 +𝜎𝑦 2 )
.
Таким образом, мы доказали, что сумма двух случайных величин,
подчиненных нормальным законам, есть нормальная случайная величина с
математическим ожиданием 𝑎𝑧 = 𝑎𝑥 + 𝑎𝑦 и дисперсией 𝜎𝑧 = √𝜎𝑥 2 + 𝜎𝑦 2 .
2)
Отношение
двух
независимых
нормальных
случайных
величин.
Отношение 𝑋/𝑌 независимых нормально распределенных случайных
величин с нулевым математическим ожиданием имеет распределение Коши. Это
можно доказать следующим образом. Пусть 𝑋 и 𝑌 имеют математическое
ожидание 0 и дисперсии 𝜎𝑥 и 𝜎𝑦 соответственно, тогда совместная функция
плотности
вероятности
представляет
распределение:
36
собой
двумерное
нормальное
2
2
𝑥
𝑦
−[
+
]
1
2𝜎𝑥 2 2𝜎𝑦 2
𝑝(𝑥, 𝑦) =
𝑒
2𝜋𝜎𝑥 𝜎𝑦
Из отношения распределений, плотность распределения 𝑈 = 𝑋/𝑌 будет
иметь вид:
∞
𝑝(𝑢) = ∫ |𝑦|𝑝(𝑢𝑦, 𝑦)𝑑𝑦 =
−∞
2
2 2
𝑦
𝑢 𝑦
∞
−[
+
]
1
2𝜎𝑦 2 2𝜎𝑥 2
=
∫ |𝑦| 𝑒
𝑑𝑦 =
2𝜋𝜎𝑥 𝜎𝑦 −∞
2
1
𝑢
∞
[−𝑦 2 (
+
)]
1
2𝜎𝑦 2 2𝜎𝑥 2
=
∫ 𝑦𝑒
𝑑𝑦.
𝜋𝜎𝑥 𝜎𝑦 0
∞
2
Необходимо учесть тот факт, что ∫0 𝑦 𝑒 −𝑎𝑦 𝑑𝑦 =
1
2𝑎
.
Тогда
𝑝(𝑢) =
1
𝜋𝜎𝑥 𝜎𝑦
1
2(
1
𝑢2
+
)
2𝜎𝑦 2 2𝜎𝑥 2
=
𝜎𝑥 𝜎𝑦
1
=
𝜋 𝑢2 𝜎𝑦 2 + 𝜎𝑥 2
𝜎𝑥
𝜎
1
𝑦
=
.
𝜋 𝑢2 + (𝜎𝑥 )2
𝜎𝑦
Полученное равенство непосредственно является распределением Коши.
То есть мы пришли к выводу, что отношение двух независимых нормальных
случайных величин с нулевыми математическими ожиданиями является
случайной величиной Коши.
3)
Случайная величина, имеющая стандартное равномерное
распределение.
Стандартное распределение Коши обладает связью со стандартным
равномерным распределением.
37
Для доказательства можно воспользоваться физической интерпретацией,
представленной на рис. 14.
1
x
Рис. 14 – График физической интерпретации
Предположим, что источник света находится на расстоянии 1 от 0 на
бесконечной прямой стене. Источник света направлен к стене под углом ,
который равномерно распределен на интервале от −
𝑥 = 𝑡𝑔(𝜃),
𝜋
2
до
𝜃 = 𝑎𝑟𝑐𝑡𝑔(𝑥)
𝑑𝜃 =
1
𝑑𝑥.
1 + 𝑥2
Поэтому распределение угла определяется как
𝑑𝜃 1 𝑑𝑥
=
.
𝜋
𝜋 1 + 𝑥2
Это нормализовано по всем углам, поэтому
𝜋
2
𝑑𝜃
=1
𝜋
− 𝜋
∫
2
и
38
𝜋
2
.
∞
1 𝑑𝑥
1
1
1 1
1
=
𝑎𝑟𝑐𝑡𝑔(∞)
−
𝑎𝑟𝑐𝑡𝑔(−∞)
=
𝜋
−
𝜋)] = 1.
[
(−
2
𝜋
1
+
𝑥
𝜋
𝜋
𝜋
2
2
−∞
∫
Тогда положение
𝑥 = 𝑡𝑔(𝜃) светового
луча имеет стандартное
распределение Коши.
4)
Сумма пуассоновских случайных величин.
Сумма двух независимых случайных величин Пуассона также является
случайной величиной Пуассона.
Пусть 𝑋 и 𝑌 независимые случайные величины, подчиняющиеся
распределению Пуассона с параметрами 𝜆1 и 𝜆2 соответственно.
Определим 𝜆 = 𝜆1 + 𝜆2 и 𝑍 = 𝑋 + 𝑌. Докажем, что 𝑍 является случайной
величиной Пуассона.
Так как 𝑋 и 𝑌 независимы, то
𝑧
𝑧
𝑗=0
𝑗=0
𝑒 −𝜆1 𝜆1 𝑗 𝑒 −𝜆2 𝜆2 𝑧−𝑗
𝑃(𝑍 = 𝑧) = ∑ 𝑃(𝑋 = 𝑗 )𝑃(𝑌 = 𝑧 − 𝑗) = ∑
=
(𝑧 − 𝑗)!
𝑗!
𝑧
𝑧
𝑗=0
𝑗=0
1
𝑧!
𝑒 −𝜆1 𝜆1 𝑗 𝑒 −𝜆2 𝜆2 𝑧−𝑗
𝑧−𝑗
−𝜆1 𝑗 −𝜆2
=∑
𝑒 𝜆1 𝑒 𝜆2
=∑
=
𝑗! (𝑧 − 𝑗)!
𝑗! (𝑧 − 𝑗)!
𝑧!
𝑧
𝑧
𝑗=0
𝑗=0
𝑧 𝑒 −𝜆1 𝜆1 𝑗 𝑒 −𝜆2 𝜆2 𝑧−𝑗 𝑒 −𝜆
𝑧
= ∑( )
=
∑ ( ) 𝜆1 𝑗 𝜆2 𝑧−𝑗 =
𝑗
𝑧!
𝑧!
𝑗
𝑒 −𝜆
𝑒 −𝜆 𝜆𝑧
𝑧
=
(𝜆 + 𝜆2 ) =
.
𝑧! 1
𝑧!
В итоге мы показали, что сумма двух независимых пуассоновских
случайных величин есть случайная величина Пуассона.
Этот метод работает и в общем. Как только становится известно для двух,
то можно продолжить и для n. Так если 𝑋1 , 𝑋2 , … , 𝑋𝑛 – независимые
пуассоновские случайные величины с параметрами 𝜆1 , 𝜆2 , … , 𝜆𝑛 соответственно,
то случайная величина 𝑋1 + 𝑋2 + ⋯ + 𝑋𝑛 также является пуассоновской
случайной величиной с параметром 𝜆1 + 𝜆2 + ⋯ + 𝜆𝑛 .
39
ЗАКЛЮЧЕНИЕ
В
результате
выполнения
дипломной
работы
были
изучены
распределения вероятностей случайных величин. Также в работе рассмотрены
основные дискретные и абсолютно непрерывные распределения случайных
величин, а именно биномиальное, пуассоновское, геометрическое, нормальное,
экспоненциальное, равномерное, распределение Коши, распределение Лапласа,
логнормальное, бета-распределение, распределение 𝜒 2 , гамма-распределение,
распределение
Фишера,
распределение
Стьюдента
и
распределение
Колмогорова.
Для проверки гипотез о виде распределения были изучены и применены
критерий согласия Колмогорова, критерий согласия хи-квадрат и критерий
согласия хи-квадрат для сложной гипотезы. Практическая реализация проверки
гипотез о виде распределения выполнена в программе STATISTICA. Результаты
проверки показали, что генерация выборок определенного распределения
моделируется корректно.
В ходе проверки взаимосвязей между распределениями случайных
величин были сделаны следующие выводы:
-
сумма двух случайных величин, подчиненных нормальным законам
является нормальной случайной величиной,
-
результатом отношение двух независимых нормальных случайных
величин будет случайная величина Коши,
-
стандартное распределение Коши напрямую связано со стандартным
равномерным распределением,
-
сумма
пуассоновских
случайных
пуассоновской случайной величиной.
40
величин
также
является
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Вентцель Е.С. Теория вероятностей: Учеб. Для вузов. 6-е изд.
стер. М.: Высш. шк., 1999.
2. Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.:
Высш. шк. 1984.
3. Лазакович
Н.В.,
Сташуленок
С.П.,
Яблонский
О.Л.
Теория
вероятностей: учебник. 3-е изд., с изменен. Минск: БГУ, 2013.
4. Севастьянов Б.А. Курс теории вероятностей и математической
статистики М.: Наука. Главная редакция физико-математической
литературы, 1982.
5. Шмыров А.С., Шмыров В.А. Случайные величины и их приложения.
СПб.: 2013.
6. Ernie Pham. Some notes on the Poisson distribution, 2008.
7. Hoang Pham. Springer handbook of engineering statistics SpringerVerlag London Limited, 2006.
8. Weisstein, Erik W. Normal ratio distribution, 2003.
41