Mathcad - lab2

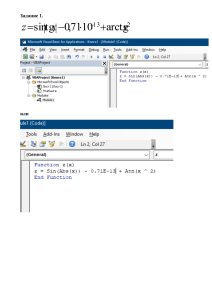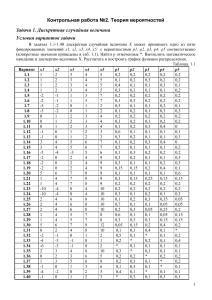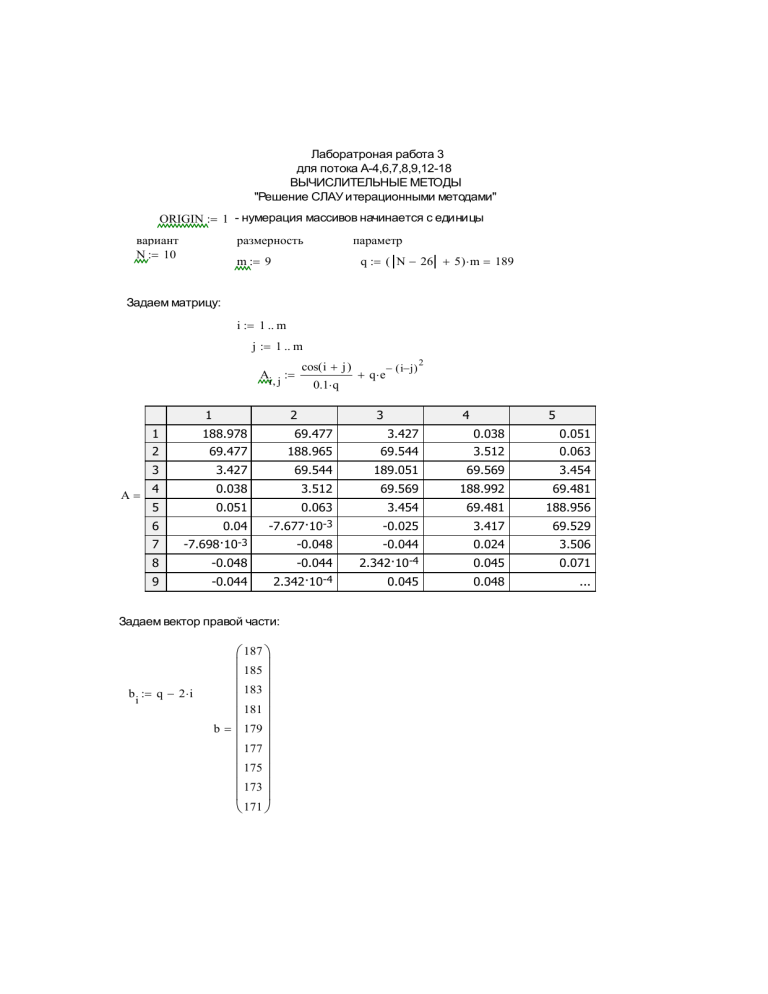
Лаборатроная работа 3
для потока А-4,6,7,8,9,12-18
ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
"Решение СЛАУ итерационными методами"
ORIGIN  1 - нумерация массивов начинается с единицы
вариант
N  10
размерность
параметр
m  9
q  ( N  26  5 )  m  189
Задаем матрицу:
i  1  m
j  1  m
A
i j
1
A
0.1 q
2
 q e
 ( i j )
3
2
4
5
1
188.978
69.477
3.427
0.038
0.051
2
69.477
188.965
69.544
3.512
0.063
3
3.427
69.544
189.051
69.569
3.454
4
0.038
3.512
69.569
188.992
69.481
5
0.051
0.063
3.454
69.481
188.956
6
0.04
-7.677·10-3
-0.025
3.417
69.529
7
-7.698·10-3
-0.048
-0.044
0.024
3.506
-0.048
-0.044
2.342·10-4
0.045
0.071
-0.044
2.342·10-4
0.045
0.048
...
8
9
Задаем вектор правой части:
b  q  2  i
i
cos( i  j )

 187 
 185 
 183 
 
 181 
b   179 
 177 
 
 175 
 173 
 171 
Преобразуем СЛАУ к виду x=Bx+c по формулам метода Якоби:
for i  1  m
PB( A m) 
for i  1  m
Pc( A b m) 
for j  1  m
b
A
B
i j

i j
c 
i
if i  j
A
i i
i
A
i i
c
B
B  PB( A m)
1
B
2
3
4
5
1
0
-0.368
-0.018
-2.028·10-4
-2.689·10-4
2
-0.368
0
-0.368
-0.019
-3.345·10-4
3
-0.018
-0.368
0
-0.368
-0.018
4
-2.028·10-4
-0.019
-0.368
0
-0.368
5
-2.69·10-4
-3.345·10-4
-0.018
-0.368
0
6
-2.11·10-4
4.061·10-5
1.316·10-4
-0.018
-0.368
7
4.073·10-5
2.551·10-4
2.348·10-4
-1.246·10-4
-0.019
8
2.551·10-4
2.35·10-4
-1.239·10-6
-2.364·10-4
-3.775·10-4
9
2.349·10-4
-1.239·10-6
-2.362·10-4
-2.54·10-4
...
c  Pc( A b m)
 0.99 
 0.979 
 0.968 


 0.958 
c   0.947 
 0.936 


 0.926 
 0.916 
 0.905 
Проверка выполнения достаточного условия сходимости:
normi( B)  0.774
или
бесконечная норма
norm1( B)  0.773
первая норма
norme( B)  1.473
евклидова норма
или
Параметры функции:
B, c - получены в результате преобразования сисемы к виду x=Bx+c;
m - размерность B;
k число совершаемых итераций;
x0 - начальное приближение.
Метод Якоби:
yakobi ( B c m k x0) 
x  x0
for n  1  k
x  B x  c
for i  1  m
rez
n i
x
i
rez
Метод Зейделя:
zeid1( B c m k x0) 
y  x0
for n  1  k
xy
for i  1  m
i
y c 
i
i
 
m
B
j1
for i  1  m
rez
n i
y
i
rez
Вычисление первой нормы вектора:
a - вектор
m - число элементов в векторе
normv1( a m) 
rez  0
for i  1  m
rez  rez  a
i
rez
Задаем начальне приближение:
x0  c
Выполняем 10 итераций по методу Якоби:
y  yakobi ( B c m 10 x0)
y
i j j
  Bij xj

ji
 0.612

 0.897
 0.729
 0.855

0.772
y
 0.834
 0.791

 0.823
 0.801

 0.818
0.241 0.22
0.217 0.215 0.213 0.211 0.225 0.551 
0.346 0.401 0.355 0.344 0.347 0.381 0.324
0.557 0.691 0.67
0.674 0.657 0.661 0.527
0.398 0.489 0.433 0.434 0.423 0.464 0.374
0.507 0.64
0.603 0.614 0.591 0.612 0.48
0.425 0.533 0.475 0.484 0.465 0.507
0.44
0.556 0.499 0.512 0.488 0.529 0.415
0.471 0.599 0.547 0.564 0.537 0.571 0.445
i  1  m
i
0.4
0.483 0.613 0.567 0.582 0.556 0.586 0.457
На 10 итерации:
x  y


0.659 
0.779 

0.699 
0.759 

0.717

0.748 
0.726 

0.742 
0.669 0.784 0.789 0.781 0.771 0.751 0.631 0.818
10 i
 0.817596 
 0.470688 
 0.598771 


 0.547235 
x   0.563796 
 0.536582 


 0.571308 
 0.444889 
 0.742486 
Проверка
 189.274 
 189.295 
 188.746 
 187.84 


A x   186.043 
 183.803 


 180.697 
 177.241 
 173.243 
Норма невязки:
r  A x  b
normv1( r m)  45.181108
 187 
 185 
 183 
 181 
 
b   179 
 177 
 
 175 
 173 
 171 
Выполняем 10 итераций по методу Зейделя:
y  zeid1( B c m 10 x0)
 0.612

 0.842
 0.796
 0.813

0.81
y
 0.811
 0.811

 0.811
 0.811

 0.811
0.447 0.42
0.38
0.422 0.416 0.412 0.424 0.741 
0.453 0.57
0.52
0.461 0.583 0.53
0.457 0.58
0.53
0.525 0.55
0.433
0.538 0.518 0.553 0.432
0.528 0.541 0.516 0.554 0.432
0.458 0.581 0.527 0.542 0.516 0.554 0.432
0.457 0.581 0.526 0.543 0.515 0.554 0.432
0.457 0.582 0.526 0.543 0.515 0.554 0.431
0.457 0.582 0.526 0.543 0.515 0.555 0.431
0.457 0.582 0.526 0.543 0.515 0.555 0.431
На 10 итерации:
i  1  m
x  y
i


0.735 
0.736 

0.736 
0.736 

0.736

0.736 
0.736 

0.736 
0.497 0.608 0.562 0.568 0.558 0.541 0.434 0.735
10 i
 0.810854 
 0.457099 
 0.581819 


 0.525583 
x   0.543034 
 0.515046 


 0.554531 
 0.431453 
 0.735873 
Проверка
 186.996 
 185.004 
 182.996 


 181.003 
A x   178.998 
 177.001 


 175 
 173 
 171 
 187 
 185 
 183 
 
 181 
b   179 
 177 
 
 175 
 173 
 171 
Норма невязки:
r  A x  b
normv1( r m)  0.018093
Решение СЛАУ с использованием встроенной в Mathcad процедуры метода Гаусса:
 0.810897 
 0.45704 
 0.581875 


 0.525538 
lsolve( A b )   0.543065 
 0.515026 


 0.554542 
 0.431448 
 0.735874 
Изменим функции для вычисления корней по методу Якоби и Зейделя, так что-бы
корни вычислялись пока не будет достигнута заданная точность
6
eps  10
Метод Якоби:
yakobi ( B c m eps x0) 
x  x0
e1 
1  norm1( B)
norm1( B)
 eps
y  B x  c
n1
while ( y  x  e1)  ( n  500 )
xy
y  B x  c
nn1
y
 
n
norm1( B)  0.773
Достаточное условие сходимости для метода Якоби
выполнено
y  yakobi ( B c m eps x0)
 0.811 
 0.457 
 0.582 
 0.526 


y   0.543 
1
 0.515 


 0.555 
 0.431 
 0.736 
y  51
2
Норма невязки:
r  A y  b
1
4
normv1( r m)  1.142171  10
norm1( B)  0.773
Метод Зейделя:
Достаточное условие сходимости для метода Зейделя
выполнено
zeid1( B c m eps x0) 
y  x0
B2  B
for i  1  m
for j  1  i
B2
i j
0
1  norm1( B)
e1 
norm1( B2)
 eps
xy
for i  1  m
i
y c 
i
i
 
m
B
y
i j j
j1
  Bij xj

ji
n1
while ( y  x  e1)  ( n  500 )
xy
for i  1  m
i
y c 
i
i
 
j1
nn1
y
 
n
y  zeid1( B c m eps x0)
 0.811 
 0.457 
 0.582 
 0.526 


y   0.543 
1
 0.515 


 0.555 
 0.431 
 0.736 
y  17
2
Норма невязки:
r  A y  b
1
5
normv1( r m)  6.948738  10
m
B
y
i j j
  Bij xj

ji
Повторим те же, действия для матрицы с размерностью 5*m:
m  5  9
q  ( N  26  5 )  m  945
i  1  m
j  1  m
A
i j

cos( i  j )
0.1 q
 q e
 ( i j )
2
b  q  2  i
i
B  PB( A m)
c  Pc( A b m)
norm1( B)  0.773
Достаточное условие для сходимости метода Якоби и метода Зейделя выполнено
Задаем начальне приближение:
y  yakobi ( B c m eps x0)
1
1
0.815
2
0.467
3
0.596
4
0.546
5
0.563
6
0.555
7
y  8
1
0.556
9
0.553
10
0.552
11
0.551
12
0.55
13
0.549
14
0.547
15
0.546
16
...
0.554
y  65
2
x0  c
Норма невязки:
r  A y  b
1
3
normv1( r m)  1.168244  10
y  zeid1( B c m eps x0)
1
1
0.815
2
0.467
3
0.596
4
0.546
5
0.563
6
0.555
7
y  8
1
0.556
9
0.553
10
0.552
11
0.551
12
0.55
13
0.549
14
0.547
15
0.546
16
...
0.554
y  19
2
Норма невязки:
r  A y  b
1
4
normv1( r m)  3.60981  10