  Числовые последовательности.

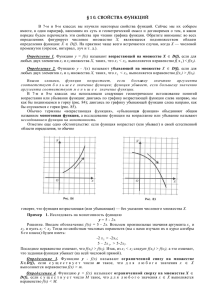
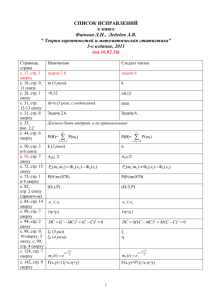
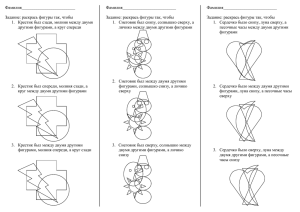
Числовые последовательности.
ОПРЕДЕЛЕНИЕ. Функцию вида y  f (x) , x   называют функцией
натурального аргумента или числовой последовательностью и
обозначают y  f (n) или y1 , y 2 , y 3 , …, y n , … . Иногда для обозначения
последовательности используется запись  y n  .
Способы задания числовой последовательности
1. Словесный способ
Правило задания последовательности описано словами, без указания
каких-то формул. Так, словесно задается последовательность простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
2. Аналитический способ
Последовательность задана аналитически, если указана формула ее n-го
члена.
Пример 1: yn  n 2 . Это аналитическое задание последовательности
1, 4, 9, 16, 25, …, n 2 , …
n , нетрудно найти член
Указав конкретное значение
последовательности с соответствующим номером. Если, например, n  9 , то
y9  9 2  81 . Напротив, если взят определенный член последовательности,
можно указать его номер. Например, если y n  625 , то из уравнения n 2  625
находим, что n  25 . Это значит, что 25-й член заданной последовательности
равен 625.
Пример 2: y n  C . Здесь речь идет о последовательности
C, C, C,...,C,...
Такую последовательность называют постоянной (или стационарной).
3. Рекуррентный способ задания последовательности состоит в том, что
указывают правило, позволяющее вычислить n-й член последовательности,
если известны ее предыдущие члены. Например, арифметическая прогрессия
– это числовая последовательность an  , заданная рекуррентно
соотношениями:
a1  a , an1  an  d
( a и d – заданные числа, d – разность арифметической прогрессии).
Задание 1. Приведите примеры последовательностей, заданных:
1) с помощью формулы n-го члена;
2) словесно;
3) рекуррентным способом.
Задание 2. Задайте последовательность аналитически и найдите первые
пять членов этой последовательности:
а) каждому натуральному числу ставится в соответствие
противоположное ему число;
б) каждому натуральному числу ставится в соответствие квадратный
корень из этого числа;
в) каждому натуральному числу ставится в соответствие половина его
квадрата.
Задание 3. По заданной формуле n-го члена вычислите первые пять
членов последовательности  y n  :
3n  1
1
n
1) y n  3  2n ;
2) yn  n 3  1; 3) y n 
; 4) y n   1  n .
2n
10
Задание 4. Выпишите первые пять членов последовательности,
заданной рекуррентно:
1) x1  2 , xn  5  xn1 ; 2) x1  4 , xn  xn1  3 ; 3) x1  5 , xn  0,5  xn1 .
Свойства числовых последовательностей
1. Последовательность  y n  называют ограниченной сверху, если все
ее члены не больше некоторого числа.
Иными словами, последовательность  y n  ограничена сверху, если
существует число М такое, что для любого n выполняется неравенство
y n  M . Число M называют верхней границей последовательности.
Например, последовательность  1,4,9,16,...,n 2 ,... ограничена
сверху. В качестве верхней границы можно взять число  1 или любое число,
которое больше, чем  1 , например 0.
2. Последовательность  y n  называют ограниченной снизу, если все
ее члены не меньше некоторого числа.
Иными словами, последовательность  y n  ограничена снизу, если
существует число m такое, что для любого n выполняется неравенство
y n  m . Число m называют нижней границей последовательности.
Например, последовательность 1,4,9,16,...,n 2 ,... ограничена снизу. В
качестве нижней границы можно взять число 1 или любое число, которое
меньше 1 .
Если последовательность ограничена и сверху, и снизу, то ее называют
ограниченной.
1 1
1
Например, 1, , ,..., ,... Эта последовательность ограничена и сверху, и
2 3
n
снизу. В качестве верхней границы можно взять число 1, в качестве нижней
границы – число 0.
Если построить график последовательности
1
1
yn  , то есть график функции y  , x   в
n
x
прямоугольной системе координат, то окажется, что
весь он расположен в полосе между некоторыми горизонтальными прямыми,
например, y  0 и y  1 , а в этом и состоит, геометрический признак
ограниченности функции.
Особенно
наглядным
становится
свойство
ограниченности
последовательности, если члены последовательности отметить точками на
числовой прямой. Ограниченность последовательности означает, что все
члены последовательности (соответствующие им точки прямой) принадлежат
некоторому отрезку.
1
Так, изобразив члены последовательности yn  точками на числовой
n
прямой, замечаем, что все они принадлежат отрезку 0,1 .
3. Последовательность  y n  называют возрастающей, если каждый
ее член больше предыдущего:
y1  y 2  y3  y 4  ...  y n  y n1  ...
Например, 1, 3, 5, 7, …, 2n  1 , … – возрастающая последовательность.
4. Последовательность  y n  называют убывающей, если каждый ее
член меньше предыдущего:
y1  y 2  y3  y 4  ...  y n  y n1  ...
1 1 1
1
Например, 1, , , , …, , … – убывающая последовательность.
n
2 3 4
Возрастающие и убывающие последовательности объединяют общим
термином – монотонные последовательности.
Задание 5. Определите, является ли последовательность  xn 
убывающей или возрастающей:
n 1
5
1
3
1) xn  3n  2 ; 2) xn  n ; 3) xn 
; 4) xn    .
n3
 3
Задание 6. Какие из заданных последовательностей ограничены сверху?
1 1 1 1 1
1 2 3 4
1)  3,2,1,0,1,...; 2) , , , , ,...; 3) , , , ,...;
2 3 4 5 6
2 3 4 5
Задание 7. Какие из заданных последовательностей ограничены снизу?
1 2 3 4
1)  1,2,3,4,5,...; 2) 5,4,3,2,1,0,1,...; 3) , , , ,...;
2 3 4 5
Задание 8. Выясните, какие из приведенных последовательностей
являются монотонными. Укажите характер монотонности:
2
1) yn  n 2  8 ; 2) yn  5 n ; 3) y n 
.
3n  1
Задание 9. Изобразите точками на числовой прямой члены
последовательности. Найдите, если возможно, отрезок, которому
принадлежат все члены последовательности:
2
n 1
1) xn  ; 2) xn 
; 3) x1  2 , xn  2  xn1 .
n
n