Показательная функция, её свойства и график

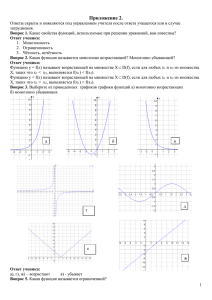
Показательная
функция, её
свойства и
график
Функция вида у = ах, где а > 0, а ≠ 1, называется
показательной функцией.
Построим графики функций
у = 2х
и
у = (1/2)х.
х
у
х
у
-3
1/8
-3
8
-2
¼
-2
4
-1
½
-1
2
0
1
0
1
1
2
1
½
2
4
2
¼
3
8
3
1/8
у = (1/2)х
у = 2х
Свойства функции у = ах, где а < 1
1. D(f) = (- ∞; + ∞);
2. не является ни чётной, ни
нечётной;
3. убывает;
4. не ограничена сверху,
ограничена снизу;
5. нет ни наибольшего, ни
наименьшего значений;
6. непрерывна;
7. E(f) = (0; +∞), ax > 0;
8. выпукла вниз.
Свойства функции у = ах, где а > 1
1. D(f) = (- ∞; + ∞);
2. не является ни чётной, ни
нечётной;
3. возрастает;
4. не ограничена сверху,
ограничена снизу;
5. нет ни наибольшего, ни
наименьшего значений;
6. непрерывна;
7. E(f) = (0; +∞), ax > 0;
8. выпукла вниз.
Логарифмическая
функция, её
свойства и
график
Функция вида у = loga x, где а > 0, а ≠ 1,
называется логарифмической функцией.
Построим графики функций
у = log2 x
и
у = log1/2 x .
х
у
х
у
1/8
-3
1/8
3
¼
-2
1/4
2
1/2
-1
1/2
1
1
0
1
0
2
1
2
-1
4
2
4
-2
8
3
8
-3
y = log2 x
y = log1/2 x
1. D(f) = (0; + ∞);
Свойства функции
у = loga x, где а > 1
2. не является ни чётной, ни
нечётной;
3. возрастает;
4. не ограничена сверху, не
ограничена снизу;
5. нет ни наибольшего, ни
наименьшего значений;
6. непрерывна;
7. E(f) = (- ∞; +∞);
8. выпукла вверх.
1. D(f) = (0; + ∞);
Свойства функции
у = loga x, где 0 < а < 1
2. не является ни чётной, ни
нечётной;
3. убывает;
4. не ограничена сверху, не
ограничена снизу;
5. нет ни наибольшего, ни
наименьшего значений;
6. непрерывна;
7. E(f) = (- ∞; +∞);
8. выпукла вниз.