Памятка Свойства функций

§ 1 0. СВОЙСТВА ФУНКЦИЙ
В 7-м и 8-м классах вы изучили некоторые свойства функций. Сейчас мы их соберем
вместе, в один параграф, напомним их суть и геометрический смысл и договоримся о том, в каком
порядке будем перечислять эти свойства при чтении графика функции. Обратите внимание: во всех
определениях фигурирует числовое множество X, являющееся подмножеством области
определения функции: X  D(f). На практике чаще всего встречаются случаи, когда X — числовой
промежуток (отрезок, интервал, луч и т. д.).
Определение 1. Функцию у = f(x) называют возрастающей на множестве X  D(f), если для
любых двух элементов х1 и х2 множества X, таких, что х1 < х2 , выполняется неравенство f( х 1 ) < f(x2).
Определение 2. Функцию у - /(х) называют убывающей на множестве X  D(f), если для
любых двух элементов х1 и х2 множества X, таких, что х 1 < х2 , выполняется неравенство f(x,) > f(x2).
Иными
словами,
функция
возрастает,
если
большему
значению
аргумента
соответствует б о л ь ш е е значение функции; функция убывает, если большему значению
аргумента соответствует м е н ь ш е е значение функции.
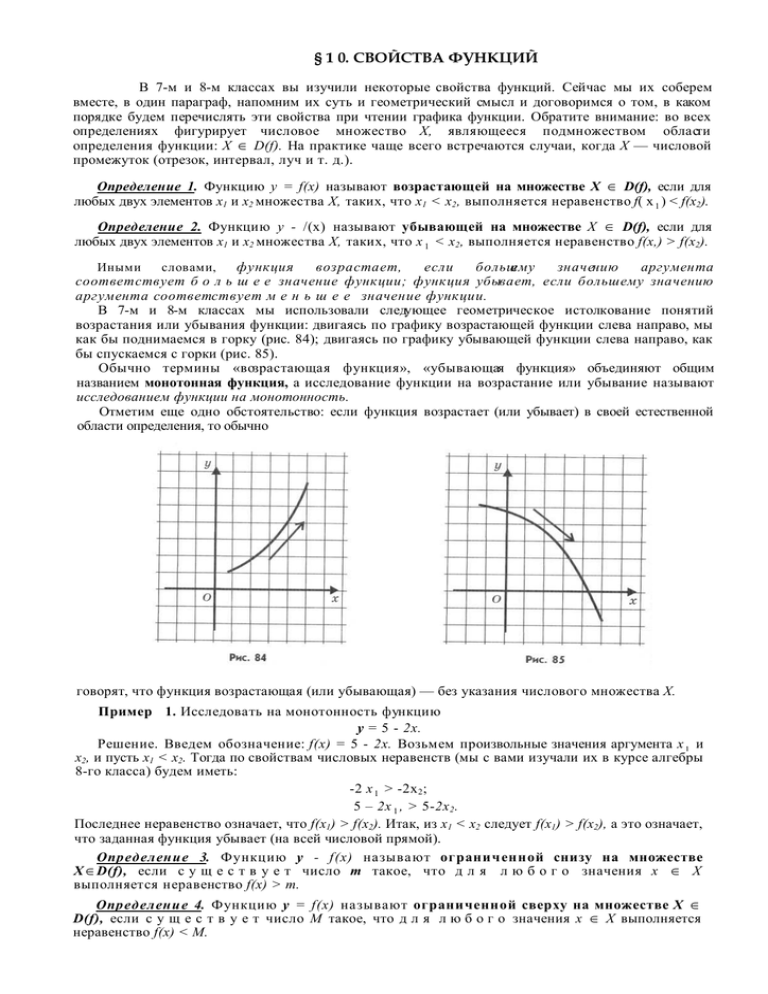
В 7-м и 8-м классах мы использовали следующее геометрическое истолкование понятий
возрастания или убывания функции: двигаясь по графику возрастающей функции слева направо, мы
как бы поднимаемся в горку (рис. 84); двигаясь по графику убывающей функции слева направо, как
бы спускаемся с горки (рис. 85).
Обычно термины «возрастающая функция», «убывающая функция» объединяют общим
названием монотонная функция, а исследование функции на возрастание или убывание называют
исследованием функции на монотонность.
Отметим еще одно обстоятельство: если функция возрастает (или убывает) в своей естественной
области определения, то обычно
говорят, что функция возрастающая (или убывающая) — без указания числового множества X.
Пример 1. Исследовать на монотонность функцию
у = 5 - 2х.
Решение. Введем обозначение: f(x) = 5 - 2х. Возьмем произвольные значения аргумента х 1 и
х2, и пусть х1 < х2. Тогда по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры
8-го класса) будем иметь:
-2 х 1 > -2х 2 ;
5 – 2х 1 , > 5-2х 2 .
Последнее неравенство означает, что f(x1) > f(x2). Итак, из х1 < х2 следует f(x1) > f(x2), а это означает,
что заданная функция убывает (на всей числовой прямой).
Определени е 3. Функцию у - f(x) называ ют ограниченной снизу на множестве
X  D(f), если с у щ е с т в у е т число т такое, что д л я л ю б о г о значения х  X
выполняется неравенство f(x) > т.
Определени е 4. Функцию у = f(x) называют ограниченной сверху на множестве X 
D(f), если с у щ е с т в у е т число М такое, что д л я л ю б о г о значения х  X выполняется
неравенство f(x) < М.
Если множество X не указано, то подразумевается, что речь идет об ограниченности функции
снизу или сверху во всей области определения.
Если функция ограничена и снизу и сверху, то ее называют ограниченной.
Ограниченность функции легко прочитывается по ее графику: функция ограничена снизу — это
значит, что ее график целиком расположен выше некоторой горизонтальной прямой у = т (рис.
86); функция ограничена сверху — это значит, что ее график целиком расположен ниже некоторой
горизонтальной прямой у = М (рис. 87).
Пример 2. Исследовать на ограниченность функцию
у=
9  х2
Р е ш е н и е . С одной стороны, вполне очевидно, что верно неравенство
9  х2
≥ 0
(по определению квадратного корня а ≥ 0). Это означает, что функция ограничена снизу (в своей
области определения, т. е. на отрезке [-3; 3]). С другой стороны, для любого х  [-3; 3] выполняется
неравенство 9 - х2 ≤ 9, а потому
9  х 2 ≤ 3 . Это означает, что функция ограничена сверху. А теперь посмотрите на график
заданной функции (см. рис. 78 на с. 92). Ограниченность функции и сверху и снизу прочитывается
по графику достаточно легко.
Определение 5. Число т называют наименьшим значением функции у = f(x) на
множестве X  D(f), если:
1) с у щ е с т в у е т число х0  X такое, что Dх0) = т;
2) д л я л ю б о г о значения х  X выполняется неравенство
f(x) ≥ f(x 1 ).
Определение 6. Число М называют наибольшим значением функции у = f(x) на множестве
X  D(f), если:
1) с у щ е с т в у е т число х0  X такое, что f(x 0 ) = М;
2) д л я л ю б о г о значения х  X выполняется неравенство
f(x) ≤ f(x 0 ).
Наименьшее значение функции мы обозначали и в 7-м, и в 8-м классах символом у наим . , а
наибольшее — символом у наиб . Если множество X не указано, то подразумевается, что речь идет об
отыскании наименьшего или наибольшего значения функции во всей области определения.
Справедливы следующие утверждения.
1) Если у функции существует у наим . , то она ограничена снизу.
2) Если у функции существует у наиб . ,то она ограничена сверху.
3) Если функция не ограничена снизу, то у наим . не существует.
4) Если функция не ограничена сверху, то у наиб . не существует.
Приведем доказательства этих утверждений.
1) Пусть у функции у - f(x) х  X есть наименьшее значение. Это значит, что существует
число х0  X такое, что для любого х е X выполняется неравенство f(x) ≥ f(x0). Это как раз и
означает, что функция ограничена снизу. Свойство 2) доказывается аналогично.
3) Доказательство проведем методом от противного. Предположим, что у наим . существует. Тогда
согласно утверждению 1) функция ограничена снизу, но это противоречит условию. Значит, наше
предположение неверно, т. е. наименьшего значения у функции нет. Свойство 4) доказывается
аналогично.
Пример 3. Найти наименьшее и наибольшее значения функции
у = 9  х2
Решение. В Примере "2 мы уже доказали,0 ≤ 9  х 2 ≤ 3, где х  [-3; 3]. Кроме того, если х =  3,
то у = 0. По определению 5 это означает, что унаим= 0. Аналогично, если х - 0, то у = 3.Поэтому унаи6 = 3.
Отметим, что полученные результаты хорошо илюстрирует график функции у = 9  х 2 (см. рис.
78).
1. Линейная функция у = кх + т
Графиком функции у = kx + т является прямая (рис. 90—92). Свойства функции у = kx + m
D(f) = 1. Линейная функция у = кх + т
Графиком функции у = kx + т является прямая (рис. 90—92). Свойства функции у = kx + m
D(f) = (-∞; +∞);
1) возрастает, если k > 0 (рис. 91), убывает, если k < 0 (рис. 92);
2) не ограничена ни снизу, ни сверху;
3) нет ни наибольшего, ни наименьшего значений;
5) функция непрерывна;
6) ?(/) = (-∞; +∞);).
4) возрастает, если k > 0 (рис. 91), убывает, если k < 0 (рис. 92);
5) не ограничена ни снизу, ни сверху;
6) нет ни наибольшего, ни наименьшего значений;
7) функция непрерывна;
8) ?(/) = (-∞; +∞);).
2. Функция у = kx2 (к  0)
Графиком функции у - kx2 является парабола с вершиной в начале координат и с ветвями,
направленными вверх, если k > О (рис. 93), и вниз, если k < 0 (рис. 94). Прямая х = 0 (ось у) является
осью параболы.
Свойства функции у= kx 2 Для случая k >0 (рис. 93):
D(f) = (- ∞; +∞));
1) убывает на луче (-°°; 0], возрастает на луче [0; +°°);
2) ограничена снизу, не ограничена сверху;
3)7 у
= 0, у . н е существует;
^ наим
наиб
5) непрерывна;
6) E{f) = [0; +оо);
7) выпукла вниз.
Обратите внимание: на промежутке (—∞; 0] функция убывает, а на промежутке [0; +∞) функция
возрастает. Эти промежутки называют промежутками монотонности функции у - kx2. Понятие
промежутка монотонности будем использовать и для других функций.
Для случая k < 0 (рис. 94):
1) D(f) = (- ∞; +∞);
2) возрастает на луче (-∞; 0], убывает на луче [0; +∞);
3) не ограничена снизу, ограничена сверху;
4) у наим = не существует, у наиб = 0;
5) непрерывна;
6) E(f) = (-∞; 0];
7) выпукла вверх.
График функции у = f(x) строится по точкам; чем больше точек вида (х; f(x)) мы возьмем, тем
более точное представление о графике получим. Если этих точек взять достаточно много, то и
представление о графике сложится более полное. Именно в этом случае интуиция и подсказывает
нам, что график надо изобразить в виде сплошной линии (в данном случае в виде параболы). А уж
затем, читая график, мы делаем выводы о непрерывности функции, о ее выпуклости вниз или вверх,
об области значений функции. Вы должны понимать, что из перечисленных семи свойств
«законными» являются лишь свойства 1), 2), 3), 4), — «законными» в том смысле, что мы в состоянии
обосновать их, ссылаясь на точные определения (ниже мы покажем это на примере функции у = л/х,
см. с. 106). Об остальных свойствах у нас имеются только наглядно-интуитивные представления.
Кстати, в этом нет ничего плохого. Из истории развития математики известно, что человечество
часто и долго пользовалось различными свойствами тех или иных объектов, не зная точных
определений. Потом, когда такие определения удавалось сформулировать, все становилось на свои места.
3. Функция у =
к
х
Графиком функции является гипербола, оси координат служат асимптотами гиперболы (рис.
95, 96).
Свойства функции у = Свойства функции у =
1) D(f) = (-∞; 0) U (0; + ∞);
к
х
2) если k > О, то функция убывает на открытом луче (-∞; 0) и на открытом луче (0; +∞) (рис. 95);
если k < О, то функция возрастает на (-∞; 0) и на (0; +∞) (рис. 96);
3) не ограничена ни снизу, ни сверху;
4) нет ни наименьшего, ни наибольшего значений;
5) функция непрерывна на открытом луче (-°°; 0) и на открытом луче (0; +∞);
6) E(f) = (-∞; 0) U (0; +∞).
4. Функция у = у х
Графиком функции является ветвь параболы (рис. 97).
Свойства функции у = х
1) D(f) = [0; +∞);
2) возрастает;
3) ограничена снизу, не ограничена сверху;
4) у наим =0, у наиб = не существует
5) непрерывна;
6) E(f) = [0; +∞);
7) выпукла вверх.
На с. 105 мы упомянули, что в принципе мы в состоянии для известных функций обосновать
свойства 1) — 4). Сделаем это в качестве примера для функции у = х Введем привычное обозначение: f(x) = х .
1) D(f) = [0; +∞). Речь идет о естественной области определения функции, т. е. об области определения выражения х . Она задается неравенством х ≥ 0, отсюда и следует, что D (f) = [0; +∞).
2) Пусть 0
х1 х г ≤ х2 . Предположим, что
х1 ≤
х 2 . Тогда
( х1 )2 > ( х 2 )2, т. е. х1 х2, что противоречит условию. Значит, наше предположение неверно, т. е.
верно неравенство х1 < х 2 .
Итак, из 0 ≤ х1 ≤ х2 следует f(x1 ) < f(x2), а это и означает, что функция возрастает на луче [0; +∞).
3) Ясно, что функция ограничена снизу, поскольку для любого
х ≥ 0 выполняется неравенство
х > 0. Докажем, что функция не ограничена сверху.
Предположим противное, что она ограничена сверху, т. е. существует положительное число М такое,
2
что для любого х > 0 выполняется неравенство х < М. Возьмем точку хо = (М + 1) . Тогда f(x0 ) =
2
х0 = (М  1) = М + 1 > М. Итак, мы предположили, что для любого х ≥ 0 выполняется
неравенство
х < М, и в то же время нашли конкретную точку х0 , в которой это неравенство не
выполняется. Полученное противоречие означает, что наше предположение неверно, а потому
функция не ограничена сверху.
4) Имеем: /(0) = 0, и для любого х ≥ 0 выполняется неравен
ство х ≥ 0. Это значит, что унаим = 0. А поскольку функция
не ограничена сверху, унаиб не существует.
5. Функция у = | х |
Графиком функции является объединение двух лучей: у = х, х ≥0 и у = -х, х ≤ 0 (рис. 98).
Свойства функции у = \ х \
1) D(f) = (-∞; +∞);
2) убывает на луче (—∞; 0], возрастает на луче [0; +∞);
3)ограничена снизу, не ограничена сверху;
4)у наим = 0, у =
5) непрерывна;
6) E(f) = [0; + ∞).
наиб
не существует;
6. Функция у = ах2 + bх + с
Граф и ком ф ун кци и яв ля ет ся парабола с в ер ш ин ой в т оч ке (х0; у0), где
и с ветвями, направленными вверх, если a > 0 (рис. 99), и вниз, если a < 0 (ри с. 100 ).
Пр я мая х =
-
b
- — явля ет ся ось ю параболы.
2a
Свойства функции у = ах2 + Ьх + с .
Для случая а > 0 (рис. 99):
1) D>(f) = (-∞; +∞);
2) убывает на луче ( - ∞; -
b
2a
 , возрастает на луче 
-
b
; +∞ );
2a
3) ограничена снизу, не ограничена сверху;
4) у наим = у 0 , у =
наиб
не существует;
5) непрерывна;
6) Е(f) = [у0; +∞);
7) выпукла вниз.
Д ЛЯ случая а < 0 (рис. 100):
1 ) D(f) = (-∞; +∞);
2) возрастает на луче ( - ∞; -
b
2a
 , убывает на луче 
3) не ограничена снизу, ограничена сверху;
4) у наим не существует , у наиб = у 0 ;
5) непрерывна;
6) Е(f) = ( -∞; у0 ;  ;
7) выпукла вверх.
-
b
; +∞ );
2a
Смотр наших знаний о функциях можно считать законченным. Разумеется, приведенным
перечнем в реальной жизни не обойтись. Некоторые новые функции и их свойства встретятся нам
уже в этой главе.
П р и м е р 5. Прочитать график функции у = f(x), заданной графически (рис. 101), где ось х —
горизонтальная асимптота графика.
Р ешен и е. Прочи тать график функции — это значит, опираясь на график, перечислить
свойства функции.
1) D(f) = [-4; +∞);
2) возрастает на отрезке [-4; 0], убывает на луче [0; +∞);
3) ограничена и снизу и сверху;
4) у наим не существует, у
5) непрерывна;
6) Е(f) = (0; 3].
наиб
= 3;