Использование графиков функций с модулем при

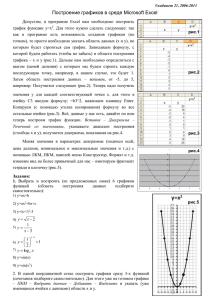
Использование графиков функций с
модулем при решении задач
Исследовательская работа
Автор: Никонов Николай, 11 класс
Научный руководитель: Атапина Елена
Никаноровна, учитель математики
МАНОУ «Лицей № 4»
Научное общество «Прорыв»
Главной целью в работе является изучение различных
способов построения графиков функций , содержащих
знак модуля и их применение при решении задач.
Задачи:
 изучить понятие функции y=|x| и её свойства;
 рассмотреть различные способы построения графиков
функций, содержащих знак модуля;
 освоить графический способ решения некоторых
задач с применением свойств функции y=|x|.
В ходе работы применялись такие методы исследования,
как изучение литературы и практический метод.
Источники
 Учебное пособие В.И.Семёнова «По страницам учебника
М.Л.Галицкого…»
 «Большая математическая энциклопедия» для школьников и
студентов;
 Математика. ЕГЭ – 2011. Типовые экзаменационные варианты. /
Под редакцией А.Л. Семенова, И.В. Ященко.
 М.Я. Выгодский. Справочник по элементарной математике
 «Новейший справочник школьника»;
 Энциклопедия «Я познаю мир» Математика;
 http://ru.wikipedia.org/wiki/Заглавная_страница;
 Карасев В.А., Левшина Г.Д. Решение задач с параметрами с
помощью графиков функций. – М.: Илекса, 2012
 СемёновВ.И. «Некоторые методические и методологические
аспекты углубленного изучения математики.9-11 классы: Учебное
пособие.. – Кемерово: Изд-во облИИУ,2001
 Понятие функции и некоторые ее свойства.
 Функция – математическое понятие, отражающее связь
между элементами различных множеств. Более точно,
это «закон», по которому каждому элементу одного
множества (называемому областью определения)
ставится в соответствие некоторый элемент другого
множества (называемого областью значений).
Существуют два определения функции:
 интуитивное определение, где понятие функции
переводится на обычный язык, используя слова
«закон», «правило» или «соответствие»;
 теоретико-множественное определение (на основе
понятия бинарного отношения), которое является
наиболее строгим (в современном представлении).
Для построения графиков функций со
знаком модуля существенными являются
следующие свойства.
Область значений функции - множество
неотрицательных чисел.
Функция является ограниченной снизу;
функция является четной, следовательно,
ее график обладает симметрией.
 Построение графиков функций, содержащих
знак модуля. Первый способ

Пример 1. Построить график функции Y=|X|
 Второй способ.
Пример 2. Построить график функции
 Y=|X|-|2-X|:

 Пример 3. Построить график функции |y+1|=2-x:
Пример 4. Найдите количество решений уравнения
𝑥 2 − 4 𝑥 +3 = 𝑎 в зависимости от значений параметра a.
Использование графиков
функций с модулем при
решении задач
Спасибо за внимание!