Построение графиков функций.

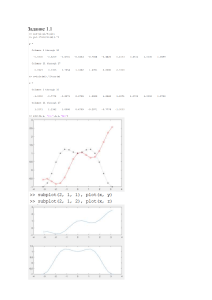
53. Построение графиков.
Задачи олимпиад на построение графиков, как правило, выходят за рамки
стандартного исследования функций. Нужно увидеть особенности, которые без
затрат на общее исследование позволяют, после преобразований (если они
необходимы) начертить эскиз графика или даже дать точное его построение. В
некоторых задачах (задачи 1-3) графики зависимостей (не функций!) имеют
необычный для школьников вид.
Задачи [5,c.13], [16,c.87], [17,c.6,7,18], [22,c.27]. Литература
Задача 1. Нарисовать эскизы графиков зависимостей:
а) 1  х 2  1  у 2  0 ;
б) |х|+| у|=1.
Решение.
а) произведение двух неотрицательных чисел равно нулю, если хотя бы один из
сомножителей равен нулю  имеем три возможных варианта:
 1  х 2  0,
 1  х 2  0,
 1  х 2  0,
1) 
2) 
3) 
 1  у 2  0,
 1  у 2  0,
 1  у 2  0.
Решением данных систем соответственно является:



 х  1,
 х  1,
 х  1,
1) 
2) 
3) 

 у  1,
 у  1.
 у  1,


у
-1
1
О
-1
Графически решение трех вариантов дает квадрат со стороной равной 2,
параллельной какой-нибудь оси координат, и с центром в начале координат.
График
Задача 2. Построить график зависимости у + | у| = х - | х|.
График
Задача 3. Построить график зависимости | y|= sin 2
x
.
2
График
Задача 4. Найдите уравнение и постройте касательную к графику функции
1
y  x 3  x 2  5 в точке с абсциссой х=3.
3
Решение:
Задача 5. Постройте график функции y 
3x  7
.
x2
Построение:
Задача 6. При каких значениях  график степенной функции у= х 2 имеет вид,
показанный на рисунке:
х
1
у
х
0
Решение. Значение  не может быть целым. Графики всех таких функций
известны, и ни один из них не имеет такого вида. Замечаем, что, судя по
рисунку, функция должна быть четной. Это означает, что если число 
представить как несократимую дробь, то числитель этой дроби должен
выражаться четным числом, а знаменатель  нечетным. Кроме этого,
производная в точке х=0, судя по рисунку, должна обращаться в бесконечность.
А это возможно только при 
Содержание: