Проект №3

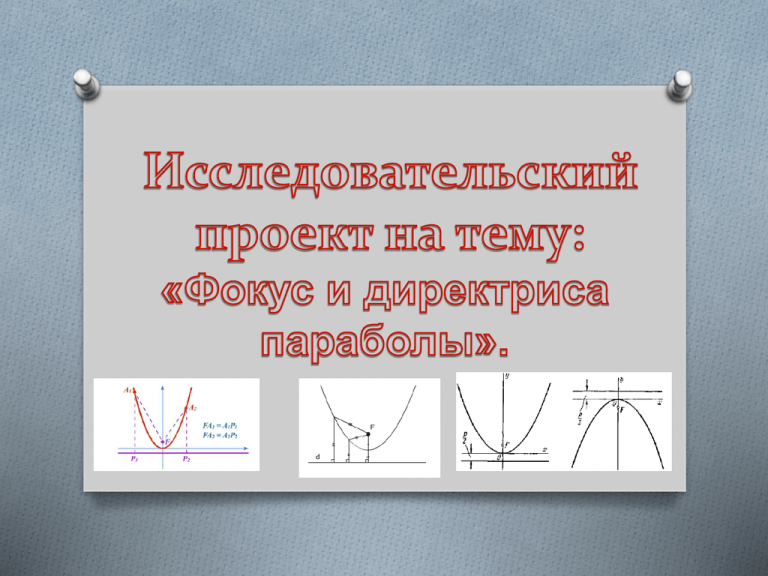
 Доказать, что геометрическое место
точек плоскости, равноудаленных от
данной точки и данной прямой,
является параболой.
 Найти фокус и директрису параболы
Расстояние от FA
равно расстоянию Аd
Расстояние
FA= (𝑥 − 𝑎)2 +(𝑦 − 𝑏)2
Расстояние
Ad= у-к
Т. к. FA=Ad, то
(𝑥 − 𝑎)2 +(𝑦 − 𝑏)2 =
(у − к)2
(𝑥 − 𝑎)2 +(𝑦 − 𝑏)2 =
(у − к)2
(𝑥 − 𝑎)2 +(𝑦 − 𝑏)2 =(у − к)2
(𝑥 − 𝑎)2 +у2 − 2уb + 𝑏 2 = у2 − 2yk + 𝑘 2
(𝑥 − 𝑎)2 −2уb + 𝑏 2 = −2yk + 𝑘 2
(𝑥 − 𝑎)2 = 2уb − 2yk − 𝑏 2 + 𝑘 2
A(𝑥 − 𝑎)2 = y − b
A (𝑥 − 𝑎)2 = y − b
(𝑥 − 𝑎)2 = 2уb − 2yk − 𝑏 2 + 𝑘 2
(𝑥 − 𝑎)2 = 2у b − k − 𝑏 2 − 𝑘 2
2
(𝑥 − 𝑎) = 2у b − k − b − k b + k
1
(𝑏 + 𝑘)
2
(𝑥 − 𝑎) = y −
2(𝑏 − 𝑘)
2
1
2(𝑏 − 𝑘)
 Директрису параболы можно найти с
помощью уравнение:
у = у0 −
р=
1
2а
р
, где р‒параметр параболы.
2
 Координаты фокуса равны
р
(х0 ;у0 + )
2
, где х0 и у0 - вершины
параболы.
𝑏
4ас−𝑏2
х0 = −
; у0 =
2𝑎
4𝑎