24 - yarkovskayaschool.ru

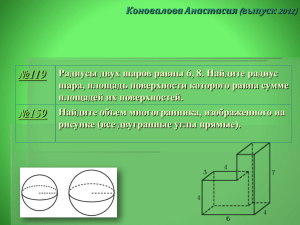
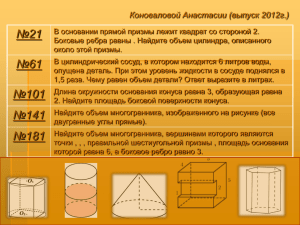
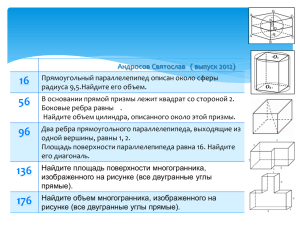
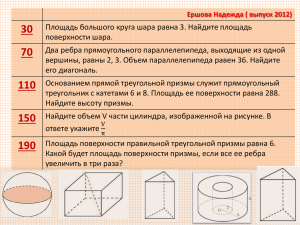
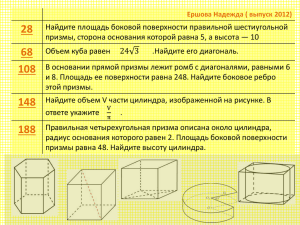
Паршин Дмитрий ( выпуск 2012)
24
В цилиндрический сосуд налили 1200 см³ воды. Уровень жидкости оказался
равным 12 см. В воду полностью погрузили деталь. При этом уровень
жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ
выразите в см³.
64
104
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра
равны 1/π . Найдите объем цилиндра, описанного около этой призмы.
144
184
Найдите площадь поверхности многогранника, изображенного на
рисунке (все двугранные углы прямые).
Через среднюю линию основания треугольной призмы, площадь боковой
поверхности которой равна 24, проведена плоскость, параллельная
боковому ребру. Найдите площадь боковой поверхности отсеченной
треугольной призмы.
Найдите объем многогранника, изображенного на рисунке (все двугранные
углы прямые).
Прототип задания B11 (№ 4907)
В цилиндрический сосуд налили 1200 см³ воды. Уровень жидкости
оказался равным 12 см. В воду полностью погрузили деталь. При
этом уровень жидкости в сосуде поднялся на 10 см. Чему равен
объем детали? Ответ выразите в см³.
Решение:
Vвытесн. жидк. = Vдетали =
=10/12 *1200 =1000
Прототип задания B11 (№ 4987)
В основании прямой призмы лежит квадрат со стороной 2.
Боковые ребра равны 1/π . Найдите объем цилиндра,
описанного около этой призмы.
.
Vц. =𝜋𝑅2 ℎ
R=
Решение:
𝒅кв 2 2
=
𝟐
2
Vц. = π ∙
= 2
1
2 ∙ =2
π
2
Прототип задания B11 (№ 5067)
Через среднюю линию основания треугольной призмы, площадь боковой
поверхности которой равна 24, проведена плоскость, параллельная
боковому ребру. Найдите площадь боковой поверхности отсеченной
треугольной призмы.
Решение:
Из соотношения подобия
треугольников в основании
призмы находим,
Pосн.отсеч.пр.
в 2р<Pисх.пр.
Верно, но
почему?
Sб.п. пропорциональна Pосн.
Sб.п.отсеч.тр.=12
Прототип задания B11 (№ 25603)
• Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы
прямые).
Решение:
S=6a²=96
Верно, но
почему?
Прототип задания B11 (№ 25691)
Найдите объем многогранника, изображенного на
рисунке (все двугранные углы прямые).
Решение:
V=2 ∙ 3 ∙ 2+1 ∙ 3 ∙ 4=24