Выпучивание продольно сжатых стержней переменной жесткости при ползучести Б.М Языев,В.И.Андреев

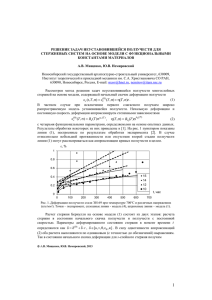
Выпучивание продольно сжатых стержней переменной жесткости при ползучести
Б.М Языев,В.И.Андреев
Подавляющее большинство исследователей рассматривают ставший «классикой»
вариант закрепления балки «шарнир-шарнир».В то же время возникает вопрос расчета
стержней при других вариантах закрепления. В данной статье приводится задача, где рассматривается условия крепления стержней типа «защемление-свободный край».
Пусть на стержень действует сила F, расчетная схема задачи представлена на рис.1.
Стержень при этом может обладать некоторой начальной погибью v0 = f (x). Размеры
стержня: d диаметр сечения, l – длина стержня. Для рассматриваемых задач в качестве
уравнения состояния принималось обобщенное нелинейное уравнение Максвелла для высокоэластических деформаций котороепринимает вид:
𝜕𝜀𝑥,𝑠 1 𝜕𝜎𝑥 𝑓∗
(1)
=
+ ∗,
𝜕𝑡
𝐸 𝜕𝑡
𝜂
где  и ε – напряжения и деформации вдоль оси x
𝐸∞
𝑓∗ = (1 +
) 𝜎 − 𝐸∞ 𝜀
𝐸
(2)
и
1 | 𝑓∗ |
= 𝑒 𝑚∗ .
𝜂∗ 𝜂∗0
1
(3)
Напомним: здесь E – модуль упругости; 0* – коэффициент начальной релаксационной вязкости; E – модуль высокоэластичности; m* – модуль скорости.
Одновременно с приложением силы в стержне возникают упругие деформации. Со
временемдеформации увеличиваются, благодаря другим составляющим общей деформации, в частности деформации ползучести. В случае наличия возмущающих факторов (эксцентриситет в приложении силы, начальный прогиб), то наряду с деформацией сжатия
имеют место и изгибные деформации, которые с течением времени приводят стержень к
разрушению.
Поскольку используемое уравнение связи для полимеров является нелинейным, то
применение наиболее общего и строгого метода в настоящий момент наталкивается на
непреодолимые математические трудности.
Систему из пяти уравнений чл.-корр. РААСН, проф. В.И. Андреев свел к двум
уравнениям относительно двух функций f* и v.
Однако разрешающие уравнения, приведенные в [1] могут быть использованы
только при применении уравнения связи Максвелла-Гуревича. Поэтому необходимо получить разрешающие уравнения, лишенные этого недостатка и подходящие под любое
уравнение связи. Опуская выводы, приведем разрешающее уравнение:
𝜕4 𝑣
𝜕
𝐹
𝜕
𝑀0
𝜕
1
+
𝑣
=
−
+
∫ 𝜀∗ 𝑟 𝑠𝑖𝑛 𝜑 𝑑𝐴].
(
)
(
)
[
𝜕𝑥4 𝜕𝑥2 𝐸𝐼(𝑥)
𝜕𝑥2
𝐸𝐼(𝑥)
𝜕𝑥2 𝐼(𝑥)
(4)
𝐴
Решение данного уравнения аналитически не представляется возможным даже в
случае значительных упрощений, вследствие его структуры решение удобно произвести
методом конечных разностей, интегрирование проводится методом Симпсона.
Рассмотрим подробно редко рассматриваемый исследователями вариант «заделка –
свободный край»
Рис. 2. ‒ Расчетная схема задачи при варианте закрепления «заделка-свободный край»
Задача. Рассматривается устойчивость стержни постоянного и переменного сечения при постоянной массе. Закрепление «свободный край -заделка» Материал ПММА.
Стержень имеет следующие расчётные параметры:l = 157мм, d0 = 15мм, F = 70кг, E =
294 кг/мм2, f0=0,15мм
Граничные условия ля защемленного конца имеем:
𝑑𝑣
𝑣 = 0,
= 0,
при 𝑥 = 0.
𝑑𝑥
На свободном конце изгибающий момент должен обратиться в нуль:
𝑑2 𝑣
𝑀 = −𝐸𝐼 2 = 0;
𝑑𝑥
Поперечная сила на верхнем конце может быть выражена через силу F и угол поворота:
𝑑𝑣
𝑑𝑀
при 𝑥 = 𝑙;
𝑄=
.
𝑑𝑥
𝑑𝑥
Выражая поперечную силу через прогиб и связывая ее с моментом имеем:
𝑄=𝐹
d2 v
𝑀 = 𝑀0 + 𝐹𝑣 = −𝐸 2 𝐼(𝑥) + 𝐸 ∫ 𝜀 ∗ 𝑟 𝑠𝑖𝑛 𝜑 𝑑𝐴
dx
𝐴
Примем за начальный прогиб
𝜋𝑥
𝑑𝑣0
𝜋
𝜋𝑥
𝑣0 = 𝑓0 (1 − 𝑐𝑜𝑠 ) ;
= 𝑓0 𝑠𝑖𝑛
;
2𝑙
𝑑𝑥
2𝑙
2𝑙
Окончательно на границе при x = l:
𝑑𝑣0
𝜋
|
= 𝑓0 ;
𝑑𝑥 (𝑥 = 𝑙)
2𝑙
𝑑𝑣
𝜋
𝑑3𝑣 𝑑2 𝑣 𝑑
𝑑
(𝐸𝐼) −
𝐹
+ 𝐹𝑓0 + 𝐸𝐼 3 + 2
[𝐸 ∫ 𝜀 ∗ 𝑟 𝑠𝑖𝑛 𝜑 𝑑𝐴] = 0.
𝑑𝑥
2𝑙
𝑑𝑥
𝑑𝑥 𝑑𝑥
𝑑𝑥
𝐴
Ответ: tкр = 2,72 часа.
Для переменного по длине стержня исходные данные:
𝑑(𝑥) = 𝑑0 − 𝑘𝑥, 𝑑(𝑙) = 0,5𝑑0 = 𝑑0 − 𝑘𝑙; 𝑘 = 0,5𝑑0⁄𝑙; 𝑑(𝑥) = 𝑑0 − 0,5𝑑0 𝑥 ⁄𝑙;
𝑙 𝜋𝑑(𝑥)2
𝑉 = ∫0
4
=
𝑙𝜋𝑑0 2
4
𝑙
∫0 (1 − 0,5𝑡)2 𝑑𝑡 = 0,583
𝑙𝜋𝑑0 2
4
; (𝑑 ′ )2 = 0,583𝑑0 2 ; (𝑑′ ) = √0,583𝑑0
а.
б
Рис. 3 Результаты расчета задачи (материал – ПММА). Рост деформаций во времени по
длине стержня (а) и рост нормальных напряжений во времени по высоте переменного сечения стержня (б)
Для стержняпеременногосечения по длине можно сказать, что прогиб стремиться к
конечному значению, и потеря устойчивости не происходит.
Литература:
1. Андреев В.И. Устойчивость полимерных стержней при ползучести: [Текст]: дис.
канд. техн. наук: 01.04.19 : защищена 22.01. / Андреев Владимир Игоревич – М., 1967.
2. Вольмир А.С. Устойчивость деформируемых систем. – М.: Наука, 1975.
3. Языев С.Б. Устойчивость стержней при ползучести с учетом начальных несовершенств[Текст]: дис. канд. техн. наук: 05.23.17 : защищена 27.10.10 : утв. 21.01.11 / Языев
Сердар Батырович – Р/н/Д., 2010. – 115 с.