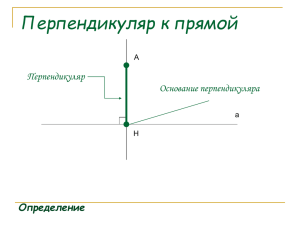
Равнобедренный треугольник и его свойства
реклама

Равнобедренный треугольник и его свойства Если две стороны и угол между ними одного треугольника соответственно равны двум сторонами и углу междутреугольника ними другогоназывается треугольника, то такие Медианой отрезок, треугольники соединяющийравны вершину треугольника с серединой противоположной стороны Отрезок биссектрисы угла , соединяющий вершину Биссектриса – луч,противоположной делящий угол на два равных угла треугольникаугла с точкой стороны, называется биссектрисой треугольника Медианы треугольника пересекаются в одной точке и точка пересечения всегда лежит внутри треугольника Дветочки, Из прямые не лежащей называются на перпендикулярными, прямой, можно провести, еслипо при крайней их пересечении мере, два образуется перпендикуляра хотя бы один к нейпрямой угол Высота Трибиссектрисы высоты треугольника треугольника – перпендикуляр, пересекаются проведенный в одной точкеиз и Три треугольника пересекаются в одной вершины она всегда лежитвсегда внутри к противоположной треугольника стороне точке и этатреугольника точка лежит внутри треугольника Е В Н К Л М И П С Д Задача 1 C 55о B Дано: Д 8 А АВД и ВСД; АД = ВС; СВД = АДВ; С = 55о; АВ = 8 см Доказать: АВД = ВСД Найти: А; СД Задача 2 В С 60о 12 А О Дано: АС ВД = О; ВО = ОС; АО = ДО С = 60о; АВ = 12 см Доказать: АВО = ДСО Д Найти: В; СД Задача 3 Дано: KMP и EFM; PM = MF; E KP = EF; NFE = TPK; P EFM = 28 см Доказать: KPM = EFM K Найти: P T P M F N KMP Какое условие необходимо добавить, чтобы доказать равенство треугольников по первому признаку равенства треугольников: 1 АС = ВD А F 2 D EM = MK E В !? DBС = ВCA С ?! 3 M FM = MN R N T ?! O K S OT – биссектриса ROS OR = OS Какие треугольники являются равнобедренными? 3 11 4 4 1 3 6 3 2 3 9 4 5 10 4 3 6 6 8 6 5 3 3 5 7 9 5 Какие из сторон являются боковыми сторонами треугольников, а какие – основанием? 4 3 1 3 основание 3 10 основание 6 2 3 3 боковая 4 5 6 4 боковая 5 Найдите равные углы в равнобедренных треугольниках: 1 2 3 4 Задача 1 В Дано: 1 2 АО = ОС; 1 = 2 Доказать: О А АВС - равнобедренный С Задача 2 В Дано: АВС - равнобедренный; АМ = NС Доказать: А M N С MBN - равнобедренный В Задача 3 D А С E Дано: АВС - равнобедренный; A = 30o Найти: DCE