ТЕПЛОВЫЕ явления Внутренняя энергия.Теплота.Работа 10
реклама

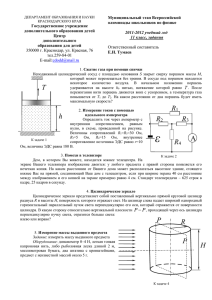
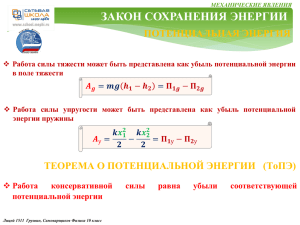
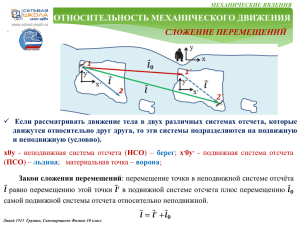
В н у т р е н н я я э н е р г и я . Т е п л о т а . Р а б о т а 10 ТЕПЛОВЫЕ ЯВЛЕНИЯ Внутренняя энергия Внутренняя энергия одноатомного идеального газа сводится к суммарной кинетической энергии поступательного движения его атомов (в модели идеального газа мы пренебрегаем взаимодействием частиц на расстоянии). Эту энергию можно найти, умножив число атомов газа 𝑁 на среднюю кинетическую энергию 𝐸 одного атома: 3 3 𝑈 = 𝑁 ∙ 𝐸 = 𝑁 ∙ 𝑘𝑇 = 𝜈𝑁𝐴 ∙ 𝑘𝑇 2 2 или 𝑈 =∙ 3𝑚 𝑅𝑇 2𝜇 Внутренняя энергия идеального газа (масса и химический состав которого неизменны) является функцией только его температуры. Внутренняя энергия реального газа, жидкости или твёрдого тела будет зависеть ещё и от объёма, т.к. при изменении объёма изменяется взаимное расположение частиц и, как следствие, потенциальная энергия их взаимодействия. Таким образом, внутренняя энергия является функцией состояния термодинамической системы: - определяется набором макроскопических параметров, например, T и V; - не зависит от того, каким образом система оказалась в данном состоянии; - если система возвращается в исходное состояние, то изменение ее внутренней энергии равно нулю. Существует два способа изменения внутренней энергии системы ۞ - совершение механической работы; ۞- передача тепла; Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ В н у т р е н н я я э н е р г и я . Т е п л о т а . Р а б о т а 10 ТЕПЛОВЫЕ ЯВЛЕНИЯ Работа ПРОДОЛЖЕНИЕ Работа в термодинамике приводит к изменению внутренней энергии термодинамической системы, а значит её температуры Причина изменения температуры в процессе сжатия газа состоит в следующем: при упругих соударениях молекул с движущимся поршнем их кинетическая энергия изменяется. Если газ сжимается, то поршень передает молекулам во время столкновений часть своей механической энергии, в результате чего газ нагревается. Поршень действует подобно футболисту, встречающему летящий мяч ударом ноги и сообщающему мячу скорость, значительно большую той, которой он обладал до удара. Если газ, напротив, расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует футболист, для того чтобы уменьшить скорость летящего мяча или остановить его; нога футболиста движется от мяча, как бы уступая ему дорогу. Работа газа над поршнем если перемещение мало и давление газа считать постоянным: 𝐴′ = 𝐹 ′ ∆𝑥 = 𝑝𝑆∆𝑥 = 𝑝∆𝑉 Работа , совершаемая поршнем над газом, отличается от работы газа А′ только знаком: 𝐴 = −𝐴′ = −𝑝∆𝑉 В общем случае давление газа не остается неизменным. В этом случае для вычисления работы нужно разделить общее изменение объема на малые части, вычислить элементарные (малые) работы, 𝑉2 а потом все их сложить. ′ 𝐴 = 𝑝 𝑉 𝑑𝑉 𝑉1 Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ В н у т р е н н я я э н е р г и я . Т е п л о т а . Р а б о т а 10 ТЕПЛОВЫЕ ЯВЛЕНИЯ Теплота ПРОДОЛЖЕНИЕ Теплопередача – это процесс перехода внутренней энергии от более горячего тела к более холодному, не связанный с совершением механической работы. Теплопередача называется еще теплообменом. Различают три вида теплопередачи: теплопроводность, конвекция и тепловое излучение Первый закон термодинамики Закон сохранения и превращения энергии, распространенный на тепловые явления. Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами 𝑸 = ∆𝑼 + 𝑨′ Работа и количество теплоты — характеристики процесса изменения энергии. В данном состоянии система всегда обладает определенной внутренней энергией. Но нельзя говорить, что в ней содержится определенное количество теплоты или работы. Как работа, так и количество теплоты являются величинами, характеризующими изменение энергии системы в результате того или иного процесса. Внутренняя энергия системы может измениться одинаково как за счет совершения системой работы, так и за счет передачи окружающим телам какого то количества теплоты Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ В н у т р е н н я я э н е р г и я . Т е п л о т а . Р а б о т а 10 ТЕПЛОВЫЕ ЯВЛЕНИЯ РЕШЕНИЕ ЗАДАЧ 10.10. Найти теплоемкость системы, состоящей из ограниченного поршнем сосуда с одноатомным газом (параметры газа р0, V0, Т0). Поршень удерживается пружиной жесткости k. Слева от поршня вакуум. Теплоемкостями сосуда, поршня и пружины пренебречь. Если газ откачать, поршень будет находиться вплотную к правой стенке цилиндра, а пружина не будет деформирована (см. рисунок). 1. Запишем условие: 2. Что такое теплоемкость? 𝑝0 𝑉0 𝑇0 k 𝐶 =? ∆𝑸 ∆𝑻 Тепло, переданное системе, может перейти во внутреннюю энергию, и пойти на ∆𝑸 = ∆𝑼 + ∆𝑨 работу, совершаемую газом: Поделив всё на ∆𝑻, получим: По определению, теплоёмкость системы равна 𝑪= 3. ∆𝑼/∆𝑻 - это теплоемкость ∆𝑼 𝟑 𝟑𝒑𝟎 𝑽𝟎 ∆𝑸 ∆𝑼 ∆𝑨 = 𝝂 𝑹 = 𝟏 =𝑪= + ∗ одноатомного газа в изохорическом ∆𝑻 𝟐 𝟐𝑻𝟎 ∆𝑻 ∆𝑻 ∆𝑻 процессе. 𝑭 𝒌𝒙 𝒑= = 𝟐 , 4. Пружина действует на поршень с силой 𝑭 = 𝒌𝒙 𝟓. Давление газа 𝑺 𝑺 где 𝑺 – площадь поршня. 6. Объем газа под поршнем 𝑽 = 𝑺𝒙 𝟑 . 𝒌𝒙𝟐 𝒌𝒙𝟐𝟎 𝒑𝑽 𝒑𝟎 𝑽𝟎 𝟐 Из 𝟐 и 𝟑 , получим: 𝒑𝑽 = 𝒌𝒙 𝟕. Работа газа ∆𝑨 = − = − 𝟐 𝟐 𝟐 𝟐 𝒑𝑽 𝒑𝟎 𝑽𝟎 𝒑𝟎 𝑽𝟎 𝑻 Из уравнения Менделеева – Клапейрона: − → ∆𝑨 = −𝟏 → 𝑻 𝑻𝟎 𝟐 𝑻𝟎 ∆𝑨 𝒑𝟎 𝑽𝟎 𝒑𝟎 𝑽𝟎 ∆𝑻 𝟑𝒑𝟎 𝑽𝟎 𝒑𝟎 𝑽𝟎 ∆𝑼 ∆𝑨 = ∆𝑨 = → + = ∆𝑻 𝟐𝑻𝟎 Теплоемкость ∗ 𝑪 = 𝟐𝑻𝟎 + = 𝟐𝑻𝟎 𝟐𝑻𝟎 ∆𝑻 ∆𝑻 𝟐𝒑𝟎 𝑽𝟎 𝟐𝒑𝟎 𝑽𝟎 = 𝑪 = ОТВЕТ: 𝑻 𝟎 Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс 𝑻 В н у т р е н н я я э н е р г и я . Т е п л о т а . Р а б о т а 10 РЕШЕНИЕ ЗАДАЧ ТЕПЛОВЫЕ ЯВЛЕНИЯ 10.13. Над одним молем идеального газа совершают замкнутый цикл, состоящий из двух изохор и двух изобар (см. рисунок). Температуры в точках 1 и 3 равны 𝑇1 и 𝑇3 соответственно. Определите работу, совершённую газом за цикл, если известно, что точки 2 и 4 лежат на одной изотерме. Т1 Т3 𝜈 А =? 1. Запишем условие: 2. Обозначим давления и объёмы в точках как: Работа на изохорах равна нулю. 𝑝2 3. Определим работу на изобаре 2 − 3, совершаемую газом: 𝑨𝟏 = 𝒑𝟐(𝑽𝟐 − 𝑽𝟏). 𝑝1 4. Воспользуемся уравнением состояния газа 𝒑𝑽 = 𝝂𝑹𝑻 в точках 2 и 3. Тогда: где T2 − температура изотермы 2 − 4 6. Полная работа, совершенная газом: Окончательно получим: 4 𝑉2 𝑨 = 𝑨𝟏 − 𝑨𝟐 = 𝝂𝑹(𝑻𝟑 + 𝑻𝟏 − 𝟐𝑻𝟐) 𝑻𝟐 = 𝑻𝟏 ∙ 𝑻𝟑 𝑨 = 𝝂𝑹 𝑻𝟑 − 𝟐 𝑻𝟏 ∙ 𝑻𝟑 + 𝑻𝟏 = Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс 1 𝑨𝟐 = 𝝂𝑹(𝑻𝟐 − 𝑻𝟏), Температуру изотермы 𝑇2 найдем, воспользовавшись законом Шарля: откуда следует: 3 𝑉1 𝑨𝟏 = 𝝂𝑹(𝑻𝟑 − 𝑻𝟐), 5. Работа на изобаре 4 − 1 совершается над газом: 2 ОТВЕТ: 𝝂𝑹 𝑨 = 𝝂𝑹 𝒑𝟐 𝑻𝟐 𝑻𝟑 = = , 𝒑𝟏 𝑻𝟏 𝑻𝟐 𝑻𝟑 − 𝑻𝟏 𝑻𝟑 − 𝑻𝟏 𝟐 𝟐