ТЕПЛОВЫЕ явления ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ 10
реклама

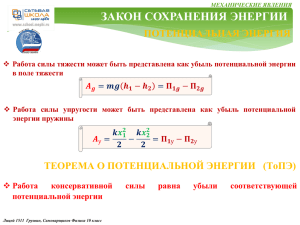
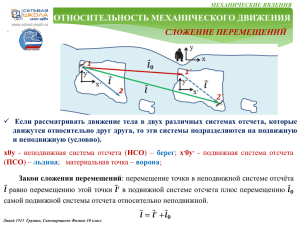
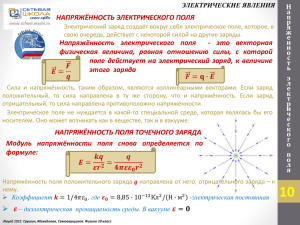
О С Н О В Ы М О Л Е К У Л Я Р Н О Й ТЕПЛОВЫЕ ЯВЛЕНИЯ Основными положениями молекулярно-кинетической теории являются следующие три утверждения: 1. Любое вещество состоит из мельчайших частиц — молекул и атомов. Они расположены в пространстве дискретно, то есть на некоторых расстояниях друг от друга. 2. Атомы или молекулы вещества находятся в состоянии беспорядочного движения, которое никогда не прекращается. 3. Атомы или молекулы вещества взаимодействуют друг с другом силами притяжения и отталкивания, которые зависят от расстояний между частицами. Идеальный газ – это газ, частицы которого являются не взаимодействующими материальными точками и испытывают только абсолютно упругие соударения друг с другом и со стенками сосуда Ф И З И К И Основные формулы молекулярной физики: 1. 𝑚 – масса вещества, 𝑉 – объем вещества, 𝜌 = 𝑚/𝑉 - плотность вещества → 𝑚 =𝜌∙𝑉 2. 𝑁 – число частиц вещества, 𝑚0 – масса одной частицы, 𝑛 = 𝑁/𝑉 концентрация вещества 𝑛 = м−3 → 𝑁 =𝑛∙𝑉 𝜌 = 𝑚𝑜 ∙ 𝑛 10 3. Из-за малых размеров атомов 𝑚0 и большого числа частиц 𝑁 используют понятие 𝜈 − количество вещества 𝜈 = моль. Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ О С Н О В Ы М О Л Е К У Л Я Р Н О Й Ф И З И К И 10 ПРОДОЛЖЕНИЕ ТЕПЛОВЫЕ ЯВЛЕНИЯ 4. Один моль – это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в 12 граммах углерода. Это число атомов называется постоянной Авогадро:𝑁𝐴 = 6,02 ∙ 1023 моль−1 → общее число частиц: 𝑁 = 𝜈 ∙ 𝑁𝐴 5. Масса одного моля вещества 𝜇 – молярная масса этого вещества . 𝜇 =кг/моль m= 𝜇 ∙ 𝜈 Термодинамической системой называется макроскопическое тело или система тел, которые могут взаимодействовать друг с другом и с окружающими телами. Термодинамическая система состоит из столь большого числа частиц, что совершенно невозможно описывать её поведение путём рассмотрения движения каждой молекулы в отдельности. Состояние термодинамической системы можно характеризовать небольшим числом макроскопических параметров величин, относящимся к системе в целом, а не к отдельным атомам или молекулам. Такими макроскопическими параметрами являются давление, температура, плотность, теплоёмкость, удельное сопротивление и т.д. Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс объём, ПРОДОЛЖЕНИЕ СЛЕДУЕТ О С Н О В Ы М О Л Е К У Л Я Р Н О Й Ф И З И К И ПРОДОЛЖЕНИЕ ТЕПЛОВЫЕ ЯВЛЕНИЯ Идеальный газ – это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками, а при взаимодействии друг с другом и со стенками сосудов испытывают абсолютно упругие соударения. Уравнение состояния идеального газа - дает взаимосвязь трех важнейших термодинамических параметров, описывающих его состояние: давления p, объема V и температуры T 𝒑𝑽 = 𝒎 𝑹𝑻 𝝁 или 𝒑𝑽 = 𝝂𝑹𝑻 Уравнение состояния идеального газа называется уравнением Менделеева Клапейрона Термодинамические процессы. Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя параметрами: давлением, объёмом и температурой, которые связаны друг с другом уравнением Менделеева – Клапейрона. Изопроцессыэ – процессы, в которых значение одного из параметров остается неизменным. Существует три вида изопроцессов. 10 Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ О С Н О В Ы М О Л Е К У Л Я Р Н О Й Ф И З И К И 10 ПРОДОЛЖЕНИЕ ТЕПЛОВЫЕ ЯВЛЕНИЯ Изотермический процесс (T = const) - квазистатический процесс, протекающий при постоянной температуре T. Из уравнения состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным: 𝒑𝑽 = 𝒄𝒐𝒏𝒔𝒕 В координатах (𝑝, 𝑉) изотермические процессы изображаются при различных значениях температуры 𝑇 семейством гипербол 𝑝 ~ 1 / 𝑉 , которые называются изотермами. В идеальных газах такие процессы подчиняется закону Бойля-Мариотта: . Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры. Изохорный процесс (V = const) - квазистатический процесс, протекающий при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным. Как следует из уравнения состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или: Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ О С Н О В Ы М О Л Е К У Л Я Р Н О Й Ф И З И К И 10 ПРОДОЛЖЕНИЕ ТЕПЛОВЫЕ ЯВЛЕНИЯ 𝒑 = 𝒄𝒐𝒏𝒔𝒕 𝑻 В координатах (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. В идеальных газах такие процессы подчиняется закону Шарля. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур Изобарный процесс (p = const) - квазистатический процесс, протекающий при постоянном объеме p и при условии, что количество вещества ν в сосуде остается неизменным. Как следует из уравнения состояния идеального газа, при этих условиях объем газа V изменяется прямо пропорционально его абсолютной температуре: V ~ T или: 𝑽 = 𝒄𝒐𝒏𝒔𝒕 𝑻 В координатах (V, T) изобарные процессы для заданного количества вещества ν при различных значениях давления p изображаются семейством прямых линий, которые называются изобарами. В идеальных газах такие процессы подчиняется закону Гей-Люссака. Большим значениям давления соответствуют изобары с меньшим наклоном по отношению к оси температур Лицей 1511 Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ О С Н О В Ы М О Л Е К У Л Я Р Н О Й Ф И З И К И 10 ТЕПЛОВЫЕ ЯВЛЕНИЯ РЕШЕНИЕ ЗАДАЧ 9.4. На рисунке изображен некоторый процесс, происходящий в идеальном газе постоянной массы. Постройте графики этого процесса в других парах переменных p p 2 3 4 5 T V 5 3 2 1 2 1 4 𝑽 = 𝝂𝑹 𝑻 𝒑 1. Изобразим pV и VT координаты; 3 4 2. Переносим на них известные данные по p и T; 3. В соответствии с уравнением 5 Менделеева - Клапейрона определим V координату минимального объема: Примечание: Она соответствует минимальному значению T и максимальному значению p , что соответствует точке 2 на исходном графике. 4. Обозначим точку 2 и уровень минимального объёма V одним делением шкалы в pV и VT координатах; 1 5. Построим процессы с учетом: T 𝒑𝑽 = 𝒄𝒐𝒏𝒔𝒕 𝑻 1 - 2. 𝒑 = 𝒄𝒐𝒏𝒔𝒕, 𝑻 ↓ в 𝟑 раза, 𝑽 ↓ в 𝟑 раза. Изобара Примечание: Точка 2 определена , поэтому строим точку 1 и процесс 1 - 2: 2 - 3. 𝒑 ↓ в 𝟐 раза, 𝑻 = 𝒄𝒐𝒏𝒔𝒕, , 𝑽 ↑ в 𝟐 раза. Изотерма 3 - 4. 𝒑 = 𝒄𝒐𝒏𝒔𝒕, 𝑻 ↑ в 𝟑 раза, 𝑽 ↑ в 𝟑 раза. Изобара 4 - 5. 𝒑 ↓ в 𝟑 раза, 𝑻 ↓ в 𝟑 раза, 𝑽 = 𝒄𝒐𝒏𝒔𝒕. Изохора Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс ПРОДОЛЖЕНИЕ СЛЕДУЕТ О С Н О В Ы М О Л Е К У Л Я Р Н О Й Ф И З И К И 10 ТЕПЛОВЫЕ ЯВЛЕНИЯ РЕШЕНИЕ ЗАДАЧ 9.20 В цилиндрическом сосуде, расположенном вертикально, находится газ массой М с молярной массой μ. Газ отделен от атмосферы поршнем, соединенным с дном сосуда растянутой пружиной жесткости. При температуре Т1 поршень расположен на высоте h от дна сосуда. До какой температуры Т2 надо нагреть газ, чтобы поршень поднялся до высоты Н? М μ K Т1 h Н Т2 =? 𝑝0 𝒑𝟏 𝑺 y Т2 Н 𝑝1 𝒑𝟎 𝑺 Т1 𝑭у𝟏 m𝒈 Мμ h 1. Запишем условие: 2. Изобразим картинку: 𝑝0 - атмосферное давление 3. Изобразим силы,, действующие на поршень в исходном состоянии: 4. Уравнение равновесия поршня в проекции на ось 0у: 𝒎 – масса поршня, 𝑝1 - давление газа под поршнем при Т1, S – площадь поршня 0𝑦| 0 = 𝑝1 𝑆 − 𝑝0 𝑆 − 𝑚𝑔 − 𝑘∆𝑙 При этом выполняется уравнение М-К: 𝑝1 𝑆ℎ = 𝜈𝑅𝑇1 5. Уравнение равновесия поршня при нагреве до Т2: 1 ∗ 2 , а также: 𝑝2 𝑆𝐻 = 𝜈𝑅𝑇2 ∗∗ (𝑝2 −𝑝1 )𝑆 = Из ∗ и ∗∗ → 0𝑦| 0 = 𝑝2 𝑆 − 𝑝0 𝑆 − 𝑚𝑔 − 𝑘(∆𝑙 + 𝐻 − ℎ) → (𝑝2 −𝑝1 )𝑆 = 𝑘(𝐻 − ℎ) 𝑀 𝑇 𝑇 𝑇2 𝑘 𝐻 − ℎ 𝑇1 Получаем: 𝑘 𝐻 − ℎ = 𝜈𝑅 2 − 1 ⟹ 𝜈 = С учетом: = + 𝜇 𝐻 ℎ 𝐻 𝜈𝑅 ℎ 𝐻𝑇1 𝜇𝑘𝐻 𝐻 − ℎ 𝑇2 = + ℎ 𝑀𝑅 Ответ: 𝑇2 = НТ 1/ℎ + µ𝑘𝐻(𝐻 − ℎ)/(𝑀𝑅) Лицей 1511. Григорьев, Грушин, Самоварщиков. Физика 10 класс Из 1 и 2