(a+bi)+(c+di) - Томский политехнический университет

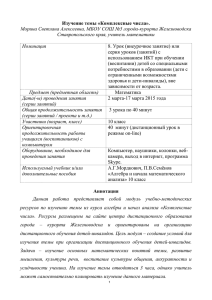
Комплексные числа
Докладчик: студент гр.2г21,
Михайлова Ксения
Томск 2013

Комплексные числа —
расширение поля вещественных чисел,
обычно обозначается «С». Любое
комплексное число может быть представлено
как формальная сумма X+iY, где X и Y —
вещественные числа, i — мнимая единица.

Комплексное число Z можно определить как
упорядоченную пару вещественных чисел
(x,y). Введём операции сложения и
умножения таких пар следующим образом:

Комплексные числа можно также определить как
семейство вещественных матриц вида

с обычным матричным сложением и умножением.
Действительной единице будет соответствовать

мнимой единице —


Ошибочно определение числа как единственного
числа, удовлетворяющего уравнению
, т.к
число
также удовлетворяет этому уравнению.
Следует также заметить, что выражение
,
ранее часто использовавшееся вместо , не вполне
корректно, т.к алгебраический корень
определяется над множеством неотрицательных
чисел. Вплоть до конца XIX века запись
вроде
считалась допустимой, но в
настоящее время, во избежание ошибок, принято
записывать это выражение как
Пример возможной ошибки при неосторожном
использовании устаревшей записи:
В то время как правильная запись приводит к
иному ответу:



Сравнение:
a+bi = c+di означает, что a=c и b=d (два
комплексных числа равны между собой тогда и
только тогда, когда равны их действительные и
мнимые части).
Сложение:
(a+bi)+(c+di)=(a+c)=(b+d)i.
Вычитание:
(a+bi)-(c+di)=(a-c)+(b-d)i.

Умножение:

Деление:

Запись комплексного числа z в виде x+iy, где
xи
- алгебраическая форма
комплексного числа.



Если вещественную X и мнимую Y части комплексного
числа выразить через модуль r=|z| и аргумент
(
,
), то всякое комплексное
число Z, кроме нуля, можно записать в
тригонометрической форме
Также может быть полезна показательная форма записи
комплексных чисел, тесно связанная с
тригонометрической через формулу Эйлера:
где
— расширение экспоненты для случая
комплексного показателя степени.

Отсюда вытекают следующие широко
используемые равенства:

Впервые, по-видимому, мнимые величины
появились в известном труде «Великое искусство,
или об алгебраических правилах» Кардано,
который счёл их непригодными к употреблению.
Пользу мнимых величин, в частности, при
решении кубического уравнения, в так
называемом неприводимом случае (когда
вещественные корни многочлена выражаются
через кубические корни из мнимых величин),
впервые оценил Бомбелли . Он же дал некоторые
простейшие правила действий с комплексными
числами.