Задача 2. - hogvards.ru

Карташян Марсел Вардгесович
Учитель математики, МБОУ г. Шахты «Гимназия им. А. С. Пушкина»,
Ростовской области
1
Кусочно-линейные функции
В данной работе рассматриваются два основных вопроса.
Первый – построение графиков функций путём представлений этих функций несколькими
линейными функциями на отдельных промежутках. Таким способом можно построить ряд
графиков функций, связанных с тригонометрическими функциями, с функциями f(x)=arcsinx,
f(x)=arccosx, f(x)=arctgx, f(x)=arcctgx, с модулями, с функциями f(x) = [x] и f(x) = {x} и т. д.
Построению графика функции предшествует исследование функции. Схема исследования
стандартна: находим область определения и область значений функции, находим также точки
пересечения графика функции с осями координат, исследуем на чётность или нечётность,
исследуем на периодичность и т. д. Построения графиков таких функций целесообразно с
применением компьютерных технологий.
Второй вопрос – обратный к первому. Функции, заданные несколькими линейными функциями на
промежутках, представляются в виде одной формулы с использованием знака модуля (с таким
представлением иногда легче исследовать на чётность, периодичность и т. д.). Если при
построении графиков функций со знаками модулей избавляемся от них, то при представлении
кусочно-линейных функций в виде одной формулы приобретаем.
Цели и задачи данной работы – создать условие для:
- свободного построения учащимися графиков кусочно-линейных функций;
- приобретения и развития умения представить некоторые сложные функции в
виде линейных функций на отдельных промежутках;
- приобретения и развития умения представить некоторые кусочно-линейные
функции в виде одной формулы.

2
Построение графиков кусочно-линейных
функций

Вначале о построении графиков функции, которые имеют вид:
k1x+b1 при x≤a1,
k2x+b2 при a1<x≤a2,
f(x)= ...…...…………………
(1)
kn-1x+bn-1 при an-2<x≤an-1,
knx+bn при x>an-1
или их можно представить в таком виде, при условии, что в
крайних точках промежутков значения линейных функций
совпадают, т. е. если yi=kiх+bi, то yi(ai)=yi+1(ai), где i =1, 2, …, n-1.
График функции состоит из n-2 отрезков и двух лучей.
Приведём примеры.
3
Построение графиков кусочно-линейных
функций
Задача 1. Построить график функции
х +4 при х ≤ - 2,
-x при -2 < x ≤ 0,
f(x)= x при 0 < x ≤ 2,
-x + 4 при x > 2.

у
2
-4
-2
0
2
х
4
рис. 1
4
Построение графиков кусочно-линейных
функций
2
2
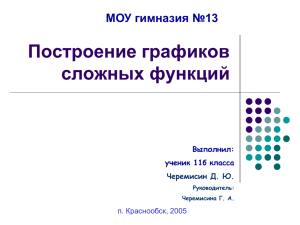
Задача 2. Построить график функции f ( x)  ( x  2)  ( x  1) .
 Представим в виде (1). f(x) = |x + 2| - |x - 1|, значит,
-3 при х ≤ -2,
f(x) = 2х + 1 при -2 < x ≤ 1,
3 при х > 1.

у
3
1
-2
0
х
1
-3
рис. 2
5
Построение графиков кусочно-линейных
функций



Задача 3. Построить график функции
f(x)=arcsin(sinx).
D(f) = R. Так как arcsin(sin(-x)) = - arcsin(sinx),
то данная функция нечётная, значит, график
функции симметричен относительно начало
координат. Функция является периодической
с основным периодом, равным 2π.
На промежутках -π/2 + 2πn ≤ x ≤ π/2 + 2πn,
nЄZ функция возрастает, а на промежутках
π/2 + 2πn ≤ x ≤ 3π/2 + 2πn, nЄZ - убывает.
siny=sinx, где -π/2 ≤ y ≤ π/2.
6
Построение графиков кусочно-линейных
функций
Представим в виде
…………………………………
x + 2π при -5π/2 < x ≤ -3π/2,
- x - π при -3π/2 < x ≤ - π/2,
x при - π/2 < x ≤ π/2,
f(x) = - x + π при π/2 < x ≤ 3π/2,
x - 2π при 3π/2 < x ≤ 5π/2 ,
-x + 2π при 5π/2 < x ≤ 7π/2,
…………………………………

Так как функция периодическая, то
достаточно построить график функции
на промежутке -π/2 ≤ x ≤ 3π/2 .
f(- π/2) = - π/2, f(π/2) = π/2, f(3π/2 ) = -π/2.
у
π/2
-π
-π/2
π/2
0
π
х
-π/2
рис. 3
7
Построение графиков кусочно-линейных
функций
Задача 4. Построить график функции f(x) = arcsin(sin |x|).
 D (f) = R, E(f) = [- π/2; π/2]. Функция чётная, следовательно,
график функции симметричен относительно оси ординат.
Поэтому достаточно построить график при х ≥ 0, а для таких
значений х f (x) = аrcsin(sinx), которая является периодической
с основным периодом, равным 2π. Используя предыдущий
пример, построим график функции.

у
π/2
-π
-π/2
π/2
0
π
х
-π/2
рис. 4
8
Построение графиков кусочно-линейных
функций
Задача 5. Построить график функции f ( x)  arccos x  arccos 1  x .
2
 D(f) = [0;1]. На этом промежутке arccos 1  x  arcsin x. В
x : arccos 1  x  arcsin x .
последнем равенстве вместо x подставим

Итак, f ( x)  arccos x  arcsin x  .
2
у
π/2

0
1
х
рис. 5
9
Построение графиков кусочно-линейных
функций

Теперь построим графики функций,
имеющих вид
k1x+b1 при x<a1,
k2x+b2 при a1<x<a2,
f(x)= ...…...………………… (2)
kn-1x+bn-1 при an-2<x<an-1,
knx+bn при x>an-1
или представляемые в виде (2).
Заметим, что D(f) = R \ {a1, a2, …, an-1}.
10
Построение графиков кусочно-линейных
функций
Задача 6. Построить график функции
 D(f) = R \ {-1; 2}. Представим f(x) в виде (2) и построим график
функции.
-x -2 при x < -1,
f(x) = x при -1 < x < 2,
x + 1 при x > 2.
у
3
2

-2
-1 0
2
х
-1
рис. 6
11
Построение графиков кусочно-линейных
функций


Задача 7. Построить график функции f(x) = arctg(tgx).
Областью определения функции является объединение промежутков
-π/2+πn < x < π/2 + πn, n Є Z или D(f) = R \ {π/2 + πn: n Є Z}. Нечётная
функция, следовательно, график симметричен относительно начала
координат. Функция является периодической с основным периодом,
равным π. На промежутках -π/2 + πn < x < π/2 + πn, n Є Z, функция
возрастает. Ввиду периодичности функции, достаточно построить
график функции на промежутке -π/2 < x < π/2.
у
π/2
- π/2
0
π/2
х
- π/2
рис. 7
12
Построение графиков кусочно-линейных
функций
Возможны примеры с комбинацией видов (1) и (2):
k1x+b1 при x≥a1,
k2x+b2 при a1<x≤a2,
k3x+b3 при a2<x≤a3,
...…...…………………
f(x)= kmx+bm при am-1<x≤am,
(3)
km+1x+bm+1 при am<x<am+1,
km+2x+bm+2 при am+1<x<am+2,
...…...…………………
knx+bn при x>an-1.
 Графики таких функций можно построить аналогично, как в
случаях (1) и (2).

13
Построение графиков кусочно-линейных
функций
Задача 8. Построить график функции
-3 при x ≤ -2,
 f(x) = 2x + 1 при -2 < x <0,
x + 2 при x > 0.

у
2
1
-2
х
-1 0
-3
рис. 8
14
Построение графиков кусочно-линейных
функций
Рассмотрим примеры, в которых соседние промежутки могут не
иметь общую граничную точку.
 Задача 9. Построить график функции
-x – 2 при x < -3,
f(x) = x + 2 при -2 ≤ x < -1,
3 при x ≥ 1.
у
3

1
-3
-2 -1
0 1
х
рис. 9
15
Построение графиков кусочно-линейных
функций
Задача 10. Построить график функции
 Найдем область определения функции:

у
3
-1 0
х
2
-1
-3
рис. 10
16
Построение графиков кусочно-линейных
функций
Задача 12. Построить график функции f(x)=arcsin(sinx)+arctg(tgx).
 Основной период функции f(x) равен 2π, поэтому построим
график только на промежутке [-π; π].

у
π
-π
-π/2
0
-π
π/2
π
х
рис. 12
17
Построение графиков кусочно-линейных
функций
Задача 13. Построить график функции f(x) = [sinx].
 Ввиду периодичности данной функции построим график на
промежутке - π ≤ x ≤ π.
-1 при - π < x < 0,
f(x) = 0 при x = - π, 0 ≤ x < π/2, π/2 < x ≤ π,
1 при x = π/2.

у
1
-π
0
π/2
π
х
-1
рис. 13
18
Построение графиков кусочно-линейных
функций
Задача 14. Построить график функции f(x) = [х3 - x].
 График данной функции построим с помощью графика функции
у = х3 - х.
у

2
1
-2
-1
0
1
2
х
-1
-2
рис. 14
19
Графическое решение уравнений
Задача 11. Решить уравнение графически
 Построим графики функций f(x) = 1 – (2/π)arccos(cosx) и
g(x)=cosx, которые являются периодическими (основной
период для двух функций равен 2π). Поэтому для нахождения
корней данного уравнения достаточно построить графики на
промежутке 0 ≤ х ≤2π.
 Ответ. πn/2, n Є Z.

у
1
0
-1
π/2
π
3π/2
х
2π
рис. 11
20
Графическое решение уравнений
Задача 15. Решить уравнение графически {2x} = [x].
 Построим графики функций y = {2x} и y = [x].

у
2
1
0
- 2
-1
-0,5
0,5
-1
Ответ. 0; 0,5.
1
2
3
х
рис. 15
21
Графическое решение уравнений
Задача 16. Решить уравнение графически [cosx] = х2 + 2x – 1.
 Функция y = [cosx] является периодической с основным
периодом, равным 2π. Поэтому построим график функции на
промежутке - π ≤ x ≤ π. Тогда
Для функции y = х2 + 2x – 1 имеем
х0= - 1, у0 = - 2.
х2 + 2x – 1 = 0, х1,2= -1 ± 2 . При х=0
у = - 1.
х2 + 2x – 1 = - 1, х2 + 2x = 0,
у
x(x + 2) = 0, x = 0 или x = - 2.
Ответ. – 2; 2 - 1.
1

-π
- π/2
0
π/2
π
х
-1
рис. 16
-2
22
Уравнение с параметром
Применение компьютерных технологий часто удобно в задачах с параметром.
Задача 17. Определить число корней уравнения ||3х|-2|=x+a в
зависимости от параметра a.
 Построим график функции f(x)=||3x|-2| или

2

 3 x  2 при x   3 ,

3 x  2 при  2  x  0,

3
f ( x)  
 3 x  2 при 0  x  2 ,

3

2
3 x  2 при x  .
3

у
График функции g(x)=x+a – прямая.
3
2
3
4
2
2
1

2
3
О
2
3
х
23
Представление в виде одной формулы кусочнолинейных функций
Переходим к рассмотрению другого вопроса: как можно
несколькими формулами заданную функцию представить с
помощью одной формулы.
 Задача 18. Представить в виде одной формулы функции
<
<

>
>
<
>
<
< <
>
<
>
24
Представление в виде одной формулы кусочнолинейных функций
Представить в виде одной формулы функцию
k1x+b1 при x<a1,
k2x+b2 при a1<x<a2,
f(x)= ...…...…………………
(4)
kn-1x+bn-1 при an-2<x<an-1,
knx+bn при x>an-1
25
Представление в виде одной формулы кусочнолинейных функций

По вышеуказанной схеме:
26
Представление в виде одной формулы кусочнолинейных функций
27
Представление в виде одной формулы кусочнолинейных функций

Задача 19. Представить в виде одной формулы функцию
28
Представление в виде одной формулы кусочнолинейных функций

Задача 20. Представить в виде одной формулы функцию

Задача 21. Представить в виде одной формулы функцию
29
Литература
1.
2.
3.
4.
Ивлев Б. М., Абрамов А. М., Дудницын Ю. П.,
Шварцбурд С. И. Задачи повышенной трудности
по алгебре и началам анализа. – М. :
Просвещение, 1990
Локоть В. В. Задачи с параметрами.
Иррациональные уравнения, неравенства,
системы, задачи с модулем. -М.: АРКТИ, 2010
Фальке Л. Я., Лисничук Н. Н. и др. Изучение
сложных тем курса алгебры в средней школе. –
М.: Народное образование; Илекса; Ставрополь,
2004
Морозова В. Д. Введение в анализ – М. :
Издательство МГТУ им. Н. Э. Баумана, 2003