НАПРЯЖЁННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ Н а п
реклама
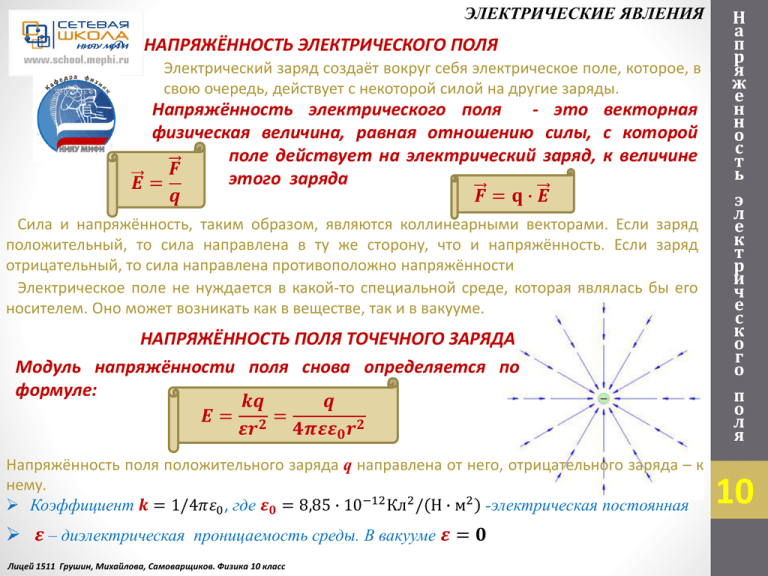
ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ НАПРЯЖЁННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ Электрический заряд создаёт вокруг себя электрическое поле, которое, в свою очередь, действует с некоторой силой на другие заряды. Напряжённость электрического поля - это векторная физическая величина, равная отношению силы, с которой поле действует на электрический заряд, к величине 𝑭 этого заряда 𝑬= 𝑭=𝐪∙𝑬 𝒒 Сила и напряжённость, таким образом, являются коллинеарными векторами. Если заряд положительный, то сила направлена в ту же сторону, что и напряжённость. Если заряд отрицательный, то сила направлена противоположно напряжённости Электрическое поле не нуждается в какой-то специальной среде, которая являлась бы его носителем. Оно может возникать как в веществе, так и в вакууме. НАПРЯЖЁННОСТЬ ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА Модуль напряжённости поля снова определяется по формуле: 𝒌𝒒 𝒒 𝑬= 𝟐= 𝜺𝒓 𝟒𝝅𝜺𝜺𝟎 𝒓𝟐 Напряжённость поля положительного заряда q направлена от него, отрицательного заряда – к нему. Коэффициент 𝒌 = 1/4𝜋𝜀0 , где 𝜺𝟎 = 8,85 ∙ 10−12 Кл2 / Н ∙ м2 -электрическая постоянная 𝜺 – диэлектрическая проницаемость среды. В вакууме 𝜺 = 𝟎 Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ Пусть заряды 𝒒𝟏 , 𝒒𝟐 , … , 𝒒𝒏 по отдельности создают в данной точке поля 𝑬𝟏 , 𝑬𝟐 , … , 𝑬𝒏 . Тогда система этих зарядов создаёт в данной точке поле 𝑬, равное векторной сумме напряжённостей полей отдельных зарядов. 𝑬 = 𝑬𝟏 + 𝑬𝟐 + ⋯ + 𝑬𝒏 ЛИНИИ НАПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ Линии напряжённости (силовые линии): идут вдоль векторов напряжённости поля; начинаются на положительных зарядах и заканчиваются на отрицательных или уходят в бесконечность; не пересекаются и не имеют изломов; В каждой точке пространства вектор напряжённости поля направлен по касательной к линии напряжённости. Линии напряжённости как бы подстраиваются под векторы напряжённости, обтекая их по касательной. +𝒒 Линии напряжённости поля отрицательно заряженной плоскости Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс Линии напряжённости поля точечного положительного заряда −𝝈 Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ РЕШЕНИЕ ЗАДАЧ 15.1. Начертить примерную картину силовых линий электрического поля, созданного двумя точечными зарядами: a) +q, +2q; б) +q, -2q. 1. Изобразим поле заряда +q, используя 4 линии: 2. Изобразим поле заряда -2q, используя 8 линий: 3. Изобразим картину поля двух зарядов: o - предположим, что точечные заряды находятся - -2q на небольшом расстоянии a друг от друга + +q o - на расстоянии 3a - 4a от зарядов картина поля подобна полю заряда, равного алгебраической сумме двух зарядов 3. Изобразим картину поля зарядов +q и +2q: 4. Изобразим картину поля зарядов +q и -2q: - на расстоянии ~3a от зарядов на ∞ - на расстоянии ~ 3a от зарядов на ∞ 4 линии 12 линий 4 линии поля между зарядами + +q a + +2q Линии поля Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс + +q a - -2q Линии поля Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ ПОТОК ВЕКТОРА НАПРЯЖЕННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 𝑬 ∆𝑺 площадка 𝜶 𝑛 Поток вектора напряженности ∆𝜱 через площадку ∆𝑺 равен скалярному произведению векторов ∆𝑺 и 𝑬 Линии поля ∆𝜱 = ∆𝑺 ∙ 𝑬 = ∆𝑺 ∙ 𝑬 ∙ 𝒄𝒐𝒔𝜶 𝐸 величина напряженности 𝑛 вектор нормали к площадке ∆𝑺 = ∆𝑺 ∙ 𝒏, 𝒏 - единичный вектор ⊥ площади Угол 𝜶- угол между ∆𝑺 и 𝑬 или 𝒏 и 𝑬; площадки ∆𝑺; 𝑬 - напряжённость электрического поля в зоне площадки ∆𝑺; ТЕОРЕМА ГАУССА Поток вектора напряженности ∆𝜱 через замкнутую поверхность пропорционален сумме зарядов 𝑸, находящихся внутри этой поверхности 𝟒𝝅𝒌𝑸 𝑸 ∆𝜱 = = 𝜺 𝜺𝜺𝟎 А попроще?? 𝜺𝟎 - электрическая постоянная, 𝜺 – диэлектрическая проницаемость среды. Алгебраическая сумма силовых линий, проходящих через замкнутую поверхность, зависит только от величины заряда, находящегося внутри этой поверхности и не зависит от формы поверхности и от местоположения заряда внутри неё . Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс Выходящие линии учитываются со «плюс», входящие – со знаком «минус». знаком Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ РЕШЕНИЕ ЗАДАЧ 15.18. В равномерно заряженном с объемной плотностью ρ шаре вырезали сферическую полость радиуса 𝑟, центр которой находится на расстоянии 𝑎 от центра шара (см рисунок). Найти напряженность 𝐸 электрического поля внутри полости вдоль прямой, соединяющей центр полости и центр шара. Радиус шара 𝑅. 1. Запишем краткое условие 𝑅, 𝑟, 𝑎, 2. Определим напряженность поля внутри шара, 𝑅 𝑟 𝑟 равномерно заряженного положительным зарядом 𝜌 с объемной плотностью ρ: 𝐸 х 𝑎 0 х Внутри шара сформируем поверхность радиусом 𝑟 𝟎<𝒓<𝑹 𝑬(𝒓) 3. Определим величину электрического заряда внутри выделенной поверхности: 𝟒 𝒒 = 𝝆 ∙ 𝑽 = 𝝆 ∙ 𝝅𝒓𝟑 𝒒 4. Определим напряженность поля 𝑬 𝒓 на 𝟑 𝑬 𝒓 ∙ 𝟒𝝅𝒓𝟐 = → выделенной поверхности по теореме Гаусса: 𝜺 𝟎 4𝜋𝑟 3 𝜌 𝜌𝑟 →𝐸 𝑟 = = ∎ Вектор напряженности 𝑬 направлен от центра шара 3𝜀0 4𝜋𝑟 2 3𝜀0 5. Внутри шара, равномерно заряженного положительным зарядом с объемной плотностью ρ разместим маленький шар, радиусом 𝑟 равномерно заряженным отрицательным зарядом с такой же плотностью ρ: В зоне наложения зарядов образуется пространство с нулевым зарядом, что равносильно наличию полости внутри большого шара Напряженность поля внутри большого можно определить используя принцип суперпозиции ПРОДОЛЖЕНИЕ СЛЕДУЕТ Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ РЕШЕНИЕ ЗАДАЧ 15.18. В равномерно заряженном с объемной плотностью ρ шаре вырезали сферическую полость радиуса 𝑟, центр которой находится на расстоянии 𝑎 от центра шара (см рисунок). Найти напряженность 𝐸 электрического поля внутри полости вдоль прямой, соединяющей центр полости и центр шара. Радиус шара 𝑅. ПРОДОЛЖЕНИЕ 𝑅, 𝑟, 𝑎, 𝜌 𝐸 х 6. Увеличим картинку: 𝑟 𝑅 0 𝑎 𝑟 Вектор напряженности 𝑟 х 0 𝑬 = 𝑬𝑹 + 𝑬𝒓 1 𝑎 𝑬𝒙 = 𝑬𝑹𝒙 + 𝑬𝒓𝒙 𝑬 𝒓 = В соответствии с ∎ : 7. Определим напряженность поля между точками 1 и а: 𝑬𝑹 и 𝑬𝒓 ⇉ - совпадают по направлению → х 2 при 𝑎 − 𝑟 < 𝑥 < 𝑎 𝐸 𝑥 = 8. Определим напряженность поля между точками a и 2: 𝝆𝒓 𝟑𝜺𝟎 𝜌𝑥 𝜌 𝑎 − 𝑥 𝝆𝒂 + = 3𝜀0 3𝜀0 𝟑𝜺𝟎 при 𝑎 < 𝑥 < 𝑎 + 𝑟 𝜌𝑥 𝜌 𝑥 − 𝑎 𝝆𝒂 − = 3𝜀0 3𝜀0 𝟑𝜺𝟎 𝝆𝒂 𝑬 𝒙 = Таким образом, вдоль диаметра полости по 0x между точками 1 и 2 𝟑𝜺𝟎 𝑬𝑹 и 𝑬𝒓 ⇆ - противоположны по направлению → 𝐸 𝑥 = Ответ: Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс 𝑬 𝒙 = 𝝆𝒂 𝟑𝜺𝟎 Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ Е = 100 В/м 𝑞 = 10 ∙ 10−6 Кл 𝑚 = 0,1 ∙ 10−3 кг 𝛽 =? ∝=? РЕШЕНИЕ ЗАДАЧ 15.19. В однородном горизонтальном электрическом поле напряженности Е = 100 В/м на двух легких вертикальных нитях удерживается заряженный шарик массой 𝑚 = 0,1 г и зарядом 𝑞 = 10 мкКл (см. рисунок). Нижнюю нить пережигают. Определить максимальный угол 𝛽, на который отклонится шарик сразу же после пережигания нити, и угол 𝛼, образуемый верхней нитью с вертикалью после того, как шарик остановится. 𝑏 2.Определим максимальный угол подъёма: 𝛽 2 𝑬 ℎ При переходе из т.1 в т.2: 𝐾1 = 𝐾2 = 0; 𝐴𝑔 = −𝑚𝑔ℎ; 𝐴 𝑇 = 0; 𝐴𝐸 = 𝑞𝐸 ∙ 𝐵; = Применим ТКЭ 𝑲𝟐 − 𝑲𝟏 = 𝑨𝒈 + 𝑨𝑻 + 𝑨𝑬 ⟹ 0 = 0 − 𝑚𝑔ℎ + 𝑞𝐸𝐵 1 ℎ = 𝑙 − 𝑙𝑐𝑜𝑠𝛽 2 1 + ⟹ 𝛽 𝛽 ∙ 𝑐𝑜𝑠 2 2 = 𝑡𝑔 𝛽 ⟹ 𝛽 2 2𝑐𝑜𝑠 2 2 2𝑠𝑖𝑛 1. Запишем краткое условие: 𝑏 = 𝑙𝑠𝑖𝑛𝛽 3 Из 1 , 2 и 3 ⟹ ⟹ 𝑚𝑔𝑙 1 − 𝑐𝑜𝑠𝛽 = 𝑞𝐸𝑙𝑠𝑖𝑛𝛽 ⟹ 𝛽 𝛽 2𝑠𝑖𝑛 ∙ 𝑐𝑜𝑠 𝑚𝑔 𝑠𝑖𝑛𝛽 2 2 ⟹ = = = 𝛽 𝛽 𝛽 𝛽 𝑞𝐸 1 − 𝑐𝑜𝑠𝛽 2 2 2 2 𝑠𝑖𝑛 + 𝑐𝑜𝑠 − 𝑠𝑖𝑛 − 𝑐𝑜𝑠 2 2 2 2 𝛽 𝑚𝑔 0,1 ∙ 10−3 ∙ 10 𝑡𝑔 = = =1⟹ 2 𝑞𝐸 10 ∙ 10−6 ∙ 100 Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс 𝛽 = 450 , 𝛽 = 900 2 ПРОДОЛЖЕНИЕ СЛЕДУЕТ Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 10 ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ Е = 100 В/м 𝑞 = 10 ∙ 10−6 Кл 𝑚 = 0,1 ∙ 10−3 кг 𝛽 =? ∝=? РЕШЕНИЕ ЗАДАЧ 15.19. В однородном горизонтальном электрическом поле напряженности Е = 100 В/м на двух легких вертикальных нитях удерживается заряженный шарик массой 𝑚 = 0,1 г и зарядом 𝑞 = 10 мкКл (см. рисунок). Нижнюю нить пережигают. Определить максимальный угол 𝛽, на который отклонится шарик сразу же после пережигания нити, и угол 𝛼, образуемый верхней нитью с вертикалью после того, как шарик остановится. ПРОДОЛЖЕНИЕ После максимального отклонения шарик возвращается в положение равновесия ∝ 𝑇 у Сила тяжести 𝑚𝑔 𝑞𝐸 𝑬 Сила натяжения нити 𝑇 𝑚𝑔 х 3.Определим угол отклонения нити в положении равновесия: 4. Определим силы, действующие на шарик: 5. Запишем уравнения динамики на оси координат: 0х│ 0 = 𝑞𝐸 − 𝑇𝑠𝑖𝑛 ∝ Сила Кулона 𝑞𝐸 0у│ 0 = 𝑇𝑐𝑜𝑠 ∝ −𝑚𝑔 𝑇𝑠𝑖𝑛 ∝= 𝑞𝐸 ⟹ ⟹ 𝑇𝑐𝑜𝑠 ∝= 𝑚𝑔 𝑞𝐸 𝑡𝑔 ∝= = 𝑚𝑔 Лицей 1511 Грушин, Михайлова, Самоварщиков. Физика 10 класс 10 ∙ 10−6 ∙ 100 =1 0,1 ∙ 10−3 ∙ 10 Ответ: 10 ∝= 450 𝜶 = 𝟒𝟓𝟎 ⟹ Н а п р я ж е н н о с т ь э л е к т р и ч е с к о г о п о л я 𝜷 = 𝟒𝟓𝟎


