Механические явления

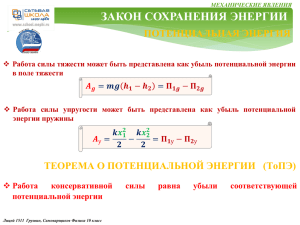
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Угловая скорость
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
Точка движется по окружности. Пусть в начальный момент времени t0 начальный радиус-вектор точки
𝒓𝟎, а угол вектора с осью 0х равен φ0 .
При равномерном движении точки радиус-вектор за любые равные
промежутки времени поворачивается на одинаковый угол, следовательно,
отношение:.
∆𝝋
𝝎=
= 𝒄𝒐𝒏𝒔𝒕
∆𝒕
у
𝒗(𝒕)
𝒗𝟎
𝒓(𝒕)
𝜑(𝑡) 𝒓
𝟎
𝜑0
х
Угловая скорость обозначается символом 𝝎 ,
размерность 𝝎 = 𝟏радиан/с
 Угловая скорость – векторная физическая величина, модуль которой равен
отношению приращения угла поворота радиуса-вектора к промежутку времени, за
который этот поворот произошел.
 Вектор 𝝎 направлен на нас, если вращение радиуса-вектора происходит в плоскости листа против
вращения часовой стрелки и обозначается ;
 Вектор 𝝎 направлен от нас, если вращение радиуса-вектора происходит в плоскости листа по
часовой стрелке и обозначается ;
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Период вращения
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
 Период вращения – промежуток времени, в течение которого радиус-вектор
совершает один оборот.
у
𝒗
𝝎

𝑹
Период вращения обозначается символом Т .
Размерность 𝐓 = 𝟏с
х
Линейная скорость
При равномерном движении по окружности модуль
скорости 𝒗 называют линейной скоростью,
чтобы отличать от угловой скорости ω.
При повороте радиуса-вектора 𝑹 на угол 2π (полный оборот), пройденный путь: 𝐬 = 𝟐𝝅𝑹, а
время, за который этот путь пройден равно Т. Тогда получим уравнения:
𝟐𝝅
𝟐𝝅𝑹
𝝎=
; и 𝒗=
,
𝑻
𝑻
из которых следует связь линейной 𝒗 и угловой 𝝎 скоростей:
𝒗=𝝎∙𝑹
 Модуль линейной скорости равен произведению модуля угловой скорости на
радиус окружности, по которой движется точка
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Ускорение при равномерном
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
движении по окружности
 Ускорение тела – векторная физическая величина, равная отношению
приращения скорости к промежутку времени, в течение которого это приращение
произошло
∆𝒗
Ускорение обозначается символом 𝒂
𝒂=
А
у
м
∆𝒕
Размерность
𝑎
=
1
𝑣𝐴
2
с
В
𝑅𝐴
𝑅𝐵
0
 Ускорение появляется не только при изменении модуля
скорости, но и при изменении её направления
∆𝑣
𝑣𝐵
х
Тело, равномерно двигаясь по окружности, в
момент времени t0 находится в точке А. Ее
радиус-вектор 𝑅 A , а скорость 𝑣A .
Через небольшой промежуток времени Δ𝑡 = 𝑡 − 𝑡0 тело будет находится в точке В. Ее
радиус-вектор 𝑅 В , а скорость 𝑣В .
За время Δt скорость изменилась на величину ∆𝑣 = 𝑣В − 𝑣A.
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
𝒂=
𝑣В − 𝑣A
t − t0
=
∆𝑣
Δt
;
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
Величина ускорения
ПРОДОЛЖЕНИЕ
Рассмотрим треугольник, составленный из векторов 𝑣A, 𝑣В и ∆𝑣
у
А
𝑅𝐴
𝑅𝐵
0
Рассмотрим треугольник со сторонами 𝑅A , 𝑅В и дугой АВ. Дуга
АВ при малых Δt тождественна отрезку АВ.
𝑣𝐴
Рассматриваемые треугольники подобны:
 они равнобедренные: 𝑅A = 𝑅В и 𝑣A = 𝑣В;
 углы при вершинах равны: 𝑅A ⊥ 𝑣A и 𝑅В ⊥ 𝑣В;
В
∆𝑣
𝑣𝐵
∆𝑣
𝑣
=
АВ
𝑅
∆𝑣 - модуль приращения вектора скорости;
Следовательно,
х
АВ = 𝑣 ∙ Δt - модуль перемещения точки за время
Δt, следовательно модуль приращения скорости равен:
Модуль ускорения равен:
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
𝒂=
𝒗𝟐
∆𝒗
=
∆𝒕
𝑹
𝑣 ∙ АВ 𝑣 2 ∙ ∆𝑡
∆𝑣 =
=
𝑅
𝑅
𝒗𝟐
𝒂𝒏 =
; 𝒂𝒏 = 𝝎𝟐 ∙ 𝑹
𝑹
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
ПРОДОЛЖЕНИЕ
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
Направление ускорения
Вектор ускорения 𝒂 направлен так
же, как и вектор ∆𝑣 - к центру
окружности.
При равномерном движении по окружности:
 скорость 𝒗 направлена по касательной к окружности и по модулю не изменяется;
 ускорение 𝒂𝒏 направлено к центру окружности и по модулю не изменяется;
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Движение колеса
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
Пусть колесо радиусом 𝑹 перемещается со скоростью 𝑉 вправо по горизонтальной поверхности.
Рассмотрим его движение в неподвижной (НСО) и в подвижной (ПСО) системах отсчета. ПСО
движется также со скоростью 𝑉.
𝑼𝑩
𝑼𝑪
C
O D
B
𝑼𝑨
A
𝑼𝑫
 В ПСО центр колеса неподвижен. Колесо вращается по часовой
стрелке вокруг центра с угловой скоростью ω, а все точки обода
будут иметь одинаковую по модулю линейную скорость 𝑈 = 𝜔 ∙ 𝑅 и
направлены по касательной.
𝟐𝝅 𝟐𝝅𝑹
𝑻=
=
𝝎
𝑼
 За один оборот нижняя точка А пройдет путь, равный длине окружности
S = 2πR. При этом будет затрачено время, равное периоду Т.
 В НСО, за время Т, равное периоду, колесо сместится на
расстояние L = 2πR,
𝑻=
𝟐𝛑𝐑 𝟐𝛑𝐑 𝟐𝝅𝑹
→
=
→𝑼=𝑽
𝐕
𝐕
𝑼
Следовательно U = V
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
C
B
O
𝑉
A
C
D
B
O
𝑉
A
D
L
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
Движение колеса
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ
ПРОДОЛЖЕНИЕ
 В соответствии с законом сложения скоростей: Скорость любой точки обода колеса в
НСО равна векторной сумме ее скорости относительно оси колеса и скорости оси колеса в
НСО
 Точки A, B, C, D равномерно вращаются вокруг
C
центра O по касательной со скоростью 𝑈
𝑈𝐶
𝑈𝐵
𝑉𝐶
𝑉𝐵
 Одновременно точки A, B, C, D движутся вправо
D
со скоростью 𝑽 = 𝑈
𝑉
B
 Относительно поверхности (точки касания A) все
O
точки движутся со скоростями 𝑉 𝑖 = 𝑈𝑖 + 𝑉
A
𝑈𝐴
𝑈𝐷 𝑉
𝐷
 Cкорость точки касания A равна 0. Она
называется - мгновенный центр вращения
𝑉𝐴 = 0
 Векторы мгновенных скоростей точек обруча будут перпендикулярны радиусвекторам, исходящим из точки А касания обручем плоскости
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
РЕШЕНИЕ ЗАДАЧ
2.18. По горизонтальной плоскости катится без скольжения с постоянной скоростью 𝜐с обруч
радиуса 𝑅. Найти скорость 𝜐 и ускорение 𝑎 точки обруча в зависимости от угла 𝜑 между вертикалью и
прямой, проведенной между точкой касания обруча с плоскостью и данной точкой обруча.
𝑣с ;
R;
𝜑;
𝑣 =?
𝑎 =?
 Запишем краткое условие в СИ:
D
 Изобразим обруч, плоскость
 Точка С (центр) обруча движется со
скоростью 𝒗𝒄
𝜑
 Произвольная точка В обруча движется со
𝜑
𝒗𝑩 скоростью 𝒖 относительно точки С.
𝑩
C
 Причем, 𝒖𝑩 = 𝒗𝒄 (*)
𝒖𝑩
𝒗𝒄
𝜑
В соответствии с законом сложения скоростей:
 Скорость точки В обруча относительно
поверхности (точки А) 𝒗𝑩 = 𝒖𝑩 + 𝒗𝒄
А
 ∠ CAB равен φ по условию → ∠ CBA также равен φ , т.к. ∆ ACB равнобедренный.
B
𝒗𝒄
 ∠ DCB равен 𝜋 − L ACB = 𝜋 − 𝜋 − 𝜑 − 𝜑 = 2𝜑
 ∠ между векторами 𝒗𝒄 и 𝒖𝑩 равен 2𝜑, т.к 𝒖𝑩 ⊥ CB, а 𝒗𝒄 ⊥ AD.
 С учетом (*) вектор 𝒗𝑩 делит угол между 𝒗𝒄 и 𝒖𝑩 пополам.
Из треугольника векторов с учетом (*) → 𝒗𝑩 = 𝒗𝒄 𝑐𝑜𝑠𝜑 + 𝒖𝑩 𝑐𝑜𝑠𝜑 = 2𝑣𝑐 𝑐𝑜𝑠𝜑
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
РЕШЕНИЕ ЗАДАЧ
ПРОДОЛЖЕНИЕ
2.18. По горизонтальной плоскости катится без скольжения с постоянной скоростью 𝜐с обруч
радиуса 𝑅. Найти скорость 𝜐 и ускорение 𝑎 точки обруча в зависимости от угла 𝜑 между вертикалью и
прямой, проведенной между точкой касания обруча с плоскостью и данной точкой обруча.
D1
 Определим ускорение точки B
𝑣с ;
B
 В некоторый момент времени 𝑡1 точка В обруча
R;
относительно поверхности (точки 𝐴1 ) движется со
𝜑;
скоростью 𝒗𝟏 под углом 𝜑 к перпендикуляру 𝐴1 D1
𝑣 =?
𝒗𝟏
𝑎 =?
𝒗𝑩𝟏 = 𝒖𝑩𝟏 + 𝒗𝒄 (1)
C
𝒗𝒄
𝜑
 Спустя время ∆t в момент времени 𝑡2 точка В обруча
относительно поверхности (точки 𝐴2 ) движется со
скоростью 𝒗𝟐 под углом 𝜑 + ∆𝜑 к перпендикуляру 𝐴2 D2
A1
D2
Приращение скорости
B
C
𝒗𝒄
𝜑 + ∆𝜑
A2
𝒗𝟐
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
𝒗𝑩𝟐 = 𝒖𝑩𝟐 + 𝒗𝒄 (2)
∆𝒗𝑩 = 𝒗𝑩𝟐 − 𝒗𝑩𝟏 = 𝒖𝑩𝟐 − 𝒖𝑩𝟏 = ∆𝒖𝑩
 Таким
образом, приращение скорости точки В
определяется только движением относительно центра
обруча (точки С) для всех точек обруча и направлено в
точку С
𝒖𝟐𝑩 𝒗𝟐𝒄
𝒂𝑩 =
=
В этом случае ускорение
𝑹
𝑹
Ответ:
𝒗𝑩 = 𝟐𝒗𝒄 𝒄𝒐𝒔𝝋
𝒗𝟐𝒄
𝒂𝑩 =
𝑹
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
РЕШЕНИЕ ЗАДАЧ
2.19. Цилиндр радиуса 𝑅 помещен между двумя параллельными рейками. Рейки движутся в одну
сторону со скоростями 𝑣1 и 𝑣2. Определить угловую скорость 𝜔 вращения цилиндра и скорость 𝑣𝐶 его
центра, если проскальзывание отсутствует.
 Изобразим цилиндр и рейки.
 Запишем краткое условие в СИ:
 Скорость точки 1 цилиндра равна скорости нижней рейки 𝒗𝟏
𝑣1;
𝑣2;
R;
𝑣𝑐 =?
𝜔 =?
2
𝒗𝟐
 Скорость точки 2 цилиндра равна скорости верхней рейки 𝒗𝟐
В соответствии с законом сложения скоростей:
𝒗𝟐 = 𝒗𝟐/с + 𝒗с (𝟐)
𝒗𝟏 = 𝒗𝟏/с + 𝒗с (𝟏)
С
 Скорость точки поверхности цилиндра относительно
𝒗𝟏
Земли равна скорости этой точки относительно центра
1
цилиндра плюс скорости центра относительно Земли
 Относительно С точки 1 и 2 движутся в противоположные стороны →
→ 𝒗𝟏/с = −𝒗𝟐/с (𝟑)
Сложим (𝟏) и (𝟐) 𝒗𝟏 + 𝒗𝟐 = 𝒗𝟏/с + 𝒗𝟐/с + 𝟐𝒗с
𝒗 𝟏 + 𝒗𝟐
𝒗 𝟏 + 𝒗𝟐
С учётом (𝟑) 𝒗с =
Т.к. точки 1 и 2 движутся в одном направлении, то: 𝒗с =
𝟐
𝟐
𝒗
+
𝒗
𝒗
−
𝒗𝟐
Относительно точки С точка 1
𝟏
𝟐
𝟏
𝒗
=
𝒗
−
𝒗
=
𝒗
−
=
𝒗𝟏/с = 𝒗𝟏 − 𝒗с или 𝟏/с
𝟏
с
𝟏
движется со скоростью (𝟏)
𝟐
𝟐
𝒗𝟏 − 𝒗𝟐
𝒗 𝟏 − 𝒗𝟐
𝝎=
→
Она связана с угловой скоростью выражением 𝒗𝟏/с = 𝝎 ∙ 𝑹 =
𝟐𝑹
𝟐
𝒗𝟏 − 𝒗𝟐
𝒗𝟏 + 𝒗𝟐
𝝎=
𝒗с =
Ответ:
Лицей 1511 Грушин, Самоварщиков Физика 10 класс
𝟐𝑹
𝟐