задания 2 турx

ВЫПОЛНИЛ
Фамилия Зиганшин
Имя Ильмир
Отчество Ильшатович
Класс 9
Школа МБОУ СОШ
Село Базгиево
Шаранский район
Ф.И.О. учителя Платонова Нурия Гильмухановна
9 класс
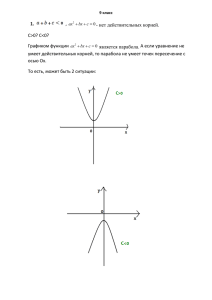
1) Известно, что 𝑎 + 𝑏 + 𝑐 < 0 и что уравнение ax 2  bx  c  0 не имеет
действительных корней. Определить знак коэффициента с.
2
𝑎 + 𝑏 + 𝑐 <0 ax  bx  c  0
Решение
Уравнение не имеет действительных корней, когда D<0
D=𝑏2 -4ac
𝑏2 -4ac<0
𝑎+𝑏+𝑐 <0
{ 2
𝑏 − 4𝑎𝑐 < 0
a+b+c<0
+
𝑏2 -4ac<0
---------------------𝑏2 +a+b+c-4ac<0
𝑏2 +a+b+c(1-4a)<0
c(1-4a)<- 𝑏2 -a-b
c< −
(𝑏2 +𝑎+𝑏)
1−4𝑎
Ответ:c<-(b^2+b+a)/(1-4a)
2) Доказать, что из любых пяти целых чисел можно выбрать три числа, сумма
которых делится на 3.
Решение. Очевидно, что любое целое число при делении на 3 даёт остаток 0, 1
или 2. Если среди данных пяти чисел найдутся три числа, имеющие различные
остатки при делении на 3, то сумма этих чисел, очевидно, делится на 3.
Если среди данных пяти чисел найдутся три числа, имеющие одинаковый
остаток при делении на 3, то сумма этих чисел, очевидно, тоже делится на 3.
Предположим теперь, что из данных пяти чисел нельзя выбрать три числа,
сумма которых делится на три. Тогда одному из остатков не будет соответствовать
ни одного числа, а каждому из двух других остатков будут соответствовать не
более двух чисел. Тогда общее количество чисел не будет превосходить 0+2+2=4, а
это противоречит тому, что всего дано, пять чисел.
3) Решить уравнение
x 2  10 x  15
3x

x 2  6 x  15 x 2  8 x  15
Пусть 𝑥 2 +15=t
𝑡−10𝑥
3𝑥
=
𝑡−6𝑥 𝑡−8𝑥
3x(t-6x)=(t-10x)(t-8x)
𝑡 2 -8tx-10tx+80𝑥 2 -3tx+18𝑥 2 =0
𝑡 2 -21tx+98𝑥 2 =0
D=(21𝑥)2 -4*1*98𝑥 2 =441𝑥 2 -392𝑥 2 =49𝑥 2
21𝑥+√49𝑥 2 21𝑥+7𝑥 28𝑥
𝑡1 =
2
=
2
=
2
=14x
21𝑥−√49𝑥 2 21𝑥−7𝑥 14𝑥
𝑡2 =
2
=
2
=
2
=7x
𝑥 2 +15=14x
𝑥 2 -14x+15=0
D=142 -4*1*15=196-60=136
14+√4∗34 14+2√34
𝑥1 =
2
=
2
=7+√34
14−√4∗34 14−2√34
=
=7-√34
2
2
𝑥2 =
𝑥 2 +15=7x
𝑥 2 -7x+15=0
D=72 -4*1*15=49-60=-11
Нет корней
Ответ: 7±√34.
3
2
4) ( 5  2 6  5  2 6 ) *
(√5 + 2√6 + √5 − 2√6)∗
√3
=(√(√3 +
2
√3
√2)2 +√(√3 − √2)2 )* 2 =
√3
√3
√3
=(√3+√2+√3 − √2)* =2√3* =3
2
2
2
=(|√3 + √2| + |√3 − √2|)*
5)
1
1
1

 ... 
1* 2 * 3 * 4 2 * 3 * 4 * 5
n(n  1)( n  2)( n  3)
Представим дробь в виде суммы дробей.
1
𝐴
= +
𝐵
+
𝐶
+
𝑛(𝑛+1)(𝑛+2)(𝑛+3) 𝑛
𝑛+1
𝑛+2
𝐷 𝐴(𝑛+1)(𝑛+2)(𝑛+3)+𝐵𝑛(𝑛+2)(𝑛+3)+𝐶𝑛(𝑛+1)(𝑛+3)+𝐷𝑛(𝑛+1)(𝑛+2)
+
=
𝑛+3
=
𝑛(𝑛+1)(𝑛+2)(𝑛+3)
𝐴(𝑛2 +3𝑛+2)(𝑛+3)+𝐵𝑛(𝑛2 +5𝑛+6)+𝐶𝑛(𝑛2 +4𝑛+3)+𝐷𝑛(𝑛2 +3𝑛+2)
=
𝑛(𝑛+1)(𝑛+2)(𝑛+3)
𝐴(𝑛3 +6𝑛2 +11𝑛+6)+𝐵(𝑛3 +5𝑛2 +6𝑛)+𝐶(𝑛3 +4𝑛2 +3)+𝐷(𝑛3 +3𝑛2 +2𝑛)
=
𝑛(𝑛+1)(𝑛+2)(𝑛+3)
𝑛3 (𝐴+𝐵+𝐶+𝐷)+𝑛2 (6𝐴+5𝐵+4𝐶+3𝐷)+𝑛(11𝐴+6𝐵+3𝐶)+2𝐷)+6𝐴
𝑛(𝑛+1)(𝑛+2)(𝑛+3)
Числитель должен быть равен 1, коэфиценты при 𝑛3 ,𝑛2 , n должны быть равны 0.
1
𝐴=
6
{
𝐴+𝐵+𝐶+𝐷 =0
𝐴=
1
6
{
−5𝐴 − 5𝐵 − 5𝐶 − 5𝐷
1
𝐴=
6
{
𝐴 − 𝐶 − 2𝐷 = 0
6𝐴 + 5𝐵 + 4𝐶 + 3𝐷 = 0 6𝐴 + 5𝐵 + 4𝐶 + 3𝐷 = 0 6𝐴 + 5𝐵 + 4𝐶 + 3𝐷 = 0
{
{
{
11𝐴 + 6𝐵 + 3𝐶 + 2𝐷 = 0 11𝐴 + 6𝐵 + 3𝐶 + 2𝐷 = 0 11𝐴 + 6𝐵 + 3𝐶 + 2𝐷 = 0
1
C=A-2D= −2D
6
1
1+5B+4( −2D) +3D=0
6
2
1+5B+ -5D=0
3
5
5B=5D−
B=D−
3
1
3
1
1 −1−2 −3
1
6
3
2
B=− − =
= =−
6
6
1
1
2 1
6
6
6 2
C= −2*− + =
11
1
1
6
3
6
+6(D− ) +3( − 2𝐷)+2D=0
11
6
1
+6D-2+ − 6𝐷 + 2𝐷=0
2
3
11
2
6
2D= −
2D=−
2D=−
D=−
2
6
1
3
1
6
1
Получаем
n=1
n=2
n=3
n=4
n=5
1
6
1
1
1
4
6
24
1
1
18
1
24
1
30
1
1
8
30 24
1
1
8
10
− +
−
−
1
10
1
12
+
+
−
1
12
1
14
1
36
−
−
1
42
48
2(𝑛+2)
−
1
6(𝑛+3)
1
−
=
1
1
1
24
6
=
2(𝑛+1)
+
1
=
1
− + −
1
−
𝑛(𝑛+1)(𝑛+2)(𝑛+3) 6𝑛
− + −
12
1
=
30
1
36
−
Сумма пяти членов равна
40
1
1
8
10
= −
=
1
1
30
1
21
−
+
−
5
48
1
36
1
42
+
−
1
14
1
48
=
1
6(𝑛+1)
+
1
3(𝑛+2)
−
1
6(𝑛+3)
сумма первых k членов заданной последовательности вычисляется по формуле.
Для суммы k+1 члена последовательности формула выполняется.
Ответ:𝑆𝑛 =
1
6(𝑛+1)
+
1
3(𝑛+2)
−
1
6(𝑛+3)
6) Мать дарит каждой из пяти своих дочерей в день ее рождения, начиная с пяти
лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют
арифметическую прогрессию, разность которой равна 2. Сколько лет было каждой
дочери, когда у них составилась библиотека общей численностью 495?
1) 5; 3; 1
2) 6; 4; 2
3) 7; 5; 3; 1
4) 8; 6; 4; 2
5) 9; 7; 5; 3; 1
6) 10; 8; 6; 4; 2
7) 11; 9; 7; 5; 3
8) 12; 10; 8; 6; 4
9) 13; 11; 9; 7; 5
10) 14; 12; 10; 8; 6
11) 15;13; 11; 9; 7
12) 16; 14; 12; 10; 8
13) 17; 15; 13; 11; 9
14) 18; 16; 14; 12; 10
Сумма 495 книг
Ответ: 10; 12; 14; 16; 18.
7 ) Пусть искомое двузначное число равно 10а+b, а - ненулевая цифра десятков, b цифра единиц
Тогда по условию должно выполнятся равенство
10а+b=a² +ab+b²
Подставляя по очереди вместо а числа от 1 до 9, и решая соответствующие квадратные
уравнения относительно b
Пусть, а=1
10+b=12 +b+𝑏 2
𝑏 2 -9=0
b=±3
b=3
13=1+1+3+9
пусть a=2
20+b=4+2b+𝑏 2
𝑏 2 +b-16=0
D=1+64=65 целых корней нет
Пусть, а=3
30а+b=9+3b+𝑏 2
𝑏 2 +2b-21=0
D=4+84=88 целых корней нет
Пусть, а=4
40+b=16+4b+𝑏 2
𝑏 2 +3b-24=0
D=9+96=105 целых корней нет
Пусть, а=5
50+b=25+5b+𝑏 2
𝑏 2 +4b-25=0 целых корней нет
Пусть, а=6
60+b=36=6b+𝑏 2
𝑏 2 +5b-24=0
D=25+96=121
𝑏1 =
−5+11
=3
2
𝑏2 =
−16
2
=-8
63
Пусть, а=7
70+b=49+4b+𝑏 2
𝑏 2 +3b-21=0
D=9+84=93 целых корней
Пусть, а=8
80+b=64+8b+𝑏 2
𝑏 2 +7b-16=0
Пусть, а=9
90+b=81+9b+𝑏 2
𝑏 2 +8b-9=0
D=64+36=100
𝑏1 =
−8+10
2
=1
91=92 +9*1+1
Ответ: 13;63;91
8) Найти последние две цифры числа
7
99
9
1) 7
2) 49
3) 343
4) 2401
5) 16807
6) 117649
7) 823543
8) 5764801
9) 40353607
10) 282475249
11) 1977326743
12) 01
13) 07
Чередуется последовательность 07, 49, 43, 01.
27) 43
Ответ: последние две цифры 43
9)
Сократить дробь:
𝑥 3 +5𝑥 2 −4𝑥−20 𝑥 2 (𝑥+5)−4(𝑥+5) (𝑥+5)(𝑥 2 −4)
= (𝑥+5)(𝑥−2) = (𝑥+5)(𝑥−2) =x+2
𝑥 2 +3𝑥−10
10) Рассмотрим любого из этих людей. Очевидно, что среди пяти остальных
у него есть либо трое знакомых, либо трое незнакомых. Можно считать, что
он знаком, по крайней мере, с тремя другими: A, B и C. Если хоть какие-то два
из них знакомы между собой, то мы получаем тройку попарно знакомых людей.
Если же они все незнакомы между собой, то мы получаем тройку попарно
незнакомых: A, B и C.