олимпиада по матемx

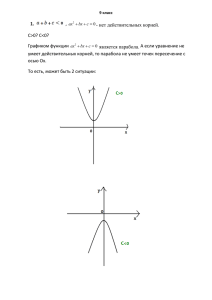
9 класс
1) Известно, что 𝑎 + 𝑏 + 𝑐 < 0 и что уравнение ax 2  bx  c  0 не имеет
действительных корней. Определить знак коэффициента с.
1 СПОСОБ:
Квадратный трехчлен f( x )= ax2 + bx + c не имеет действительных
корней, значит, он сохраняет один и тот же знак для всех x . А так как
f (1) = a + b + c < 0, то и f (0) = c < 0
Значит знак коэффициента с отрицательный.
2 СПОСОБ:
если уравнение не имеет действительных корней, то D<0
D=b^2-4ac<0
a+b+c<0 решаем систему уравнений.
сложим верхнее и нижнее уравнения: b^2-4ac+a+b+c<0
b^2+b+a+c(1-4a)<0
c(1-4a)<-(b^2+b+a)
c< - (b^2+b+a)/(1-4a)
Значит, знак коэффициента отрицательный.
2) Доказать, что из любых пяти целых чисел можно найти три, сумма которых
делится на 3.
Рассмотрим остатки от деления этих чисел на 3. Возможны два случая:
1) Найдутся три числа с одинаковым остатком. Тогда их сумма и будет делиться
на 3.
2) С каждым остатком будет не более двух чисел. Тогда, если предположить,
что всего два разных остатка, мы получим, что чисел было бы не более четырех.
Это противоречие — их у нас 5. Значит, среди них присутствуют все три разных
остатка от деления на 3. Сложив числа с остатками 0, 1 и 2, получим число,
делящееся на 3.
3) Решить уравнение:
x 2  10 x  15
3x

x 2  6 x  15 x 2  8 x  15 .
4) Упростить выражение:
( 5 2 6  5 2 6)*
3
2 .
5) Найти сумму:
1
1
1

 ... 
.
1* 2 * 3 * 4 2 * 3 * 4 * 5
n(n  1)( n  2)( n  3)
6) Мать дарит каждой из пяти своих дочерей в день ее рождения, начиная с пяти
лет, столько книг, сколько дочери лет. Возрасты пяти дочерей составляют
арифметическую прогрессию, разность которой равна 2. Сколько лет было
каждой дочери, когда у них составилась библиотека общей численностью 495?
7) Найти двухзначное число, равное неполному квадрату суммы его цифр.
Ответ: 13 и 63;
Решение: a и b искомые числа;
Должно выполняться следующее равенство:
10a+b=a^2+ab+b^2
Под это равенство подходят числа 13 и 63.
10+3=1+3+9
13=13
60+3=36+18+9
63=63.
8) Найти последние две цифры числа
7
99
9
9) Сократите дробь:
x3  5 x 2  4 x  20
x 2  3x  10
10)
Докажите, что среди любых шести человек найдутся трое знакомых или
трое незнакомых между собой людей.
Рассмотрим все случаи:
Наименьшее число знакомых – это 2. Если знакомых 2, то незнакомых 4(это
больше 3).
Если знакомых 3, то незнакомых тоже 3(числа равны 3).
Если знакомых 4 (то уже это больше 3) дальше не имеет смысла
рассматривать.