14451_no04

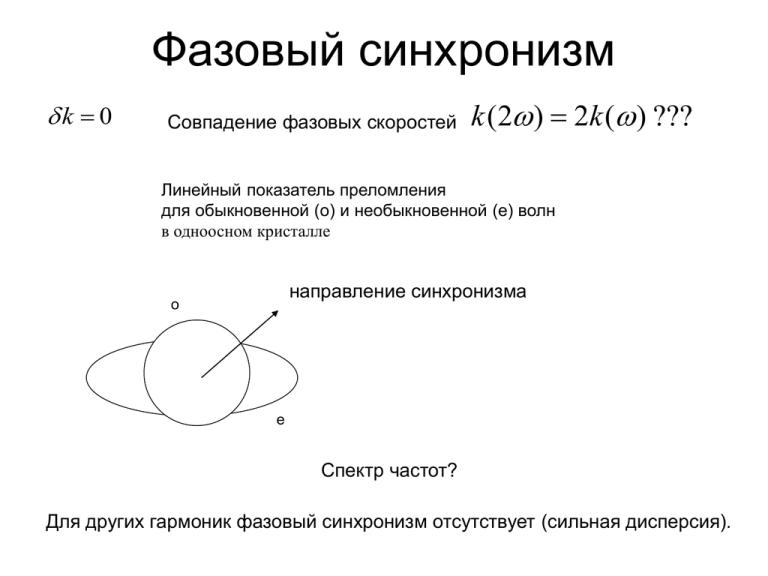
Фазовый синхронизм
k  0
Совпадение фазовых скоростей
k (2 )  2k ( ) ???
Линейный показатель преломления
для обыкновенной (o) и необыкновенной (е) волн
в одноосном кристалле
направление синхронизма
o
e
Спектр частот?
Для других гармоник фазовый синхронизм отсутствует (сильная дисперсия).
ПАРАМЕТРИЧЕСКИЕ
ВЗАИМОДЕЙСТВИЯ
В СРЕДЕ С КВАДРАТИЧНОЙ
НЕЛИНЕЙНОСТЬЮ
Взаимодействие плоских монохроматических волн в слабоанизотропной нелинейной среде
Сильная дисперсия (спектр сосредоточен вблизи нескольких частот).
Для отдельных компонент
E(r, t )  E(r, t ) exp[i(k0 z  0t )]  к.с.,
P(r, t )  P(r, t ) exp[i(k0 z  0t )]  к.с.
Квазиоптическое уравнение
 E 1 E 
 2 E
k02 
1  P 
2ik0 

 4   P  2i
    E  D2
  0.
2
 z
vg t 
t
0 
0 t 

1  dk 
1  d 2k 
1

, D2   2 
 2.

vg  d    
2  d     vg
0
0
Пренебрегаем …
E
k02
2ik0
 4  P  0
z
0
En
n
 2 i
 Pn
z
cnn
Квадратичная нелинейность
 Pi  Pi (2) ( p  q ) 

 ijk(2) ( p  q ,  p , q )E j (q ) Ek ( p )
jk ;( pq )
1  2  3
1  2  3
Волновые вектора поля
Волновые вектора для квадратичной поляризации сре
k1 (1 ), k 2 (2 ), k 3 (3 )
k p  k n (n )  k m (m )
Фиксируем поляризацию волн и привлекаем симметрию Клейнмана
  2
 k  k3 (3 )  k2 (2 )  k1 (1 )
Квазиоптические уравнения
Без поглощения
С учетом линейного поглощения
dE1
1
i
E3 E2* exp(i kz ),
dz
cn1
dE1

 i 1 E3 E2* exp(i kz )  1E1 ,
dz
cn1
dE2
2
i
E3 E1* exp(i kz ),
dz
cn2
dE2
2
i
E3 E1* exp(i kz )   2 E2 ,
dz
cn2
dE3
3
i
E1E2 exp( i kz ).
dz
cn3
dE3
3
i
E1E2 exp( i kz )  3 E3.
dz
cn3
Соотношения Мэнли-Роу
(поглощение отсутствует)
d | E1 |2
1
 2
Im[ E3 E2* E1* exp(i kz )],
dz
cn1
d | E2 |2
2
 2
Im[ E3 E2* E1* exp(i kz )],
dz
cn2
d | E3 |2
3
2
Im[ E3 E2* E1* exp(i kz )].
dz
cn3
d  n1
d  n2
d  n3
2
2
2
 | E1 |    | E2 |     | E3 | 
dz  1
dz  3
 dz  2


n1
1
| E1 ( z ) |2  | E1 ( z0 ) |2  
n2
2
| E2 ( z) |2  | E2 ( z0 ) |2  
n3
3
| E ( z ) |
2
3
0
 | E3 ( z ) |2 
Закон сохранения энергии
n1 | E1 ( z ) |2  n2 | E2 ( z ) |2  n3 | E3 ( z ) |2  const
d
2
2
2
 n1 | E1 ( z ) |  n2 | E2 ( z ) | n3 | E3 ( z ) |   0
dz
Точное решение выражается через специальные (эллиптические) функции
Качественный анализ
Два варианта соотношения интенсивностей
высокочастотной (3) и низкочастотных (1, 2) волн
Мощная низкочастотная волна
Из соотношений Мэнли-Роу
n21
n21
2
2
2
| E1 ( z ) | | E1 ( z0 ) | 
| E2 ( z ) |  | E2 ( z0 ) |  | E1 ( z0 ) | 
| E2 ( z0 ) |2 ,

n12
n12
2
2
| E1 ( z ) |2 | E1 ( z0 ) |2 
n31
n31
2
2
2
2
|
E
(
z
)
|

|
E
(
z
)
|

|
E
(
z
)
|

|
E
(
z
)
|
.


3
0
3
1 0
3
0
n13
n13
n21
n31
2
2
2
| E1 ( z0 ) | 
| E2 ( z0 ) | | E1 ( z ) | | E1 ( z0 ) | 
| E3 ( z0 ) |2
n12
n13
2
Вывод: если на входе нелинейной среды
| E1 ( z0 ) |2 | E2 ( z0 ) |2 ,| E1 ( z0 ) |2
то интенсивность мощной волны меняется при распространении
незначительно (перекачка неэффективна).
Слабые волны
n32
2
0 | E2 ( z ) | | E2 ( z0 ) | 
| E3 ( z0 ) | ,
n23
2
2
n23
2
0 | E3 ( z ) | | E2 ( z0 ) | 
| E 2 ( z0 ) | .
n32
2
2
dE2
2
i
E3 E10* exp(i kz ),
dz
cn2
dE3
3
i
E10 E2 exp( i kz ).
dz
cn3
Если на границеE2
 E3  0
то имеется нулевое решение (в отличие от ГВГ).
Решение уравнений
dE2
2
exp( i kz )
i
E3 E10* ,
dz
cn2
d 
dE2  2 * dE2
 223
2
exp(

i

kz
)

i
E


|
E
|
E2 exp( i kz )
10
10


dz 
dz 
cn2
dz
cn2n3
d 2 E2
dE2  223
2

i

k

|
E
|
E2  0
10
2
dz
dz
cn2n3
Линейное диф. уравнение с постоянными коэффициентами
E2 ~ exp(ipz )
p 2  p k 
 223
cn2n3
| E10 |2  0
p=
Решение при заданных граничных условиях …
Задание
Учесть линейное поглощение, считая
1  2   , 3  0
dE2

 i 2 E3 E10* exp(i kz )   E2 ,
dz
cn2
dE3
3
i
E10 E2 exp( i kz )   E3.
dz
cn3
Высокочастотная мощная
волна
| E30 | | E10 | ,| E20 |
2
2
2
Распадная неустойчивость
Начальный этап (заданное высокочастотное поле)
dE1
1
*
i
E30 E2 exp(i kz )   E1 ,
dz
cn1
dE2
2
i
E30 E1* exp(i kz )   E2 .
dz
cn2
Если на границе
E1  E2  0 , то имеется нулевое решение (в отличие от ГВГ).
Здесь нужны флуктуационные затравки.
Решение уравнений
E1,2  A1,2 exp( z )
dA1
1
i
E30 A2* exp(i kz ),
dz
cn1
dA2
2
i
E30 A1* exp(i kz ).
dz
cn2
d 2 A1
dA1  212
2

i

k

|
E
|
A1  0
30
2
dz
dz
cn1n2
  i k  
A1 ~ exp(z )
1,2  i
k
2

2
 212
k 
 212
cn1n2
| E30 |2  0
2
| E30 |2   
cn1n2
 2 
E1,2  A1,2 exp( z ) ~ exp[(1,2   ) z ]