14531_no12

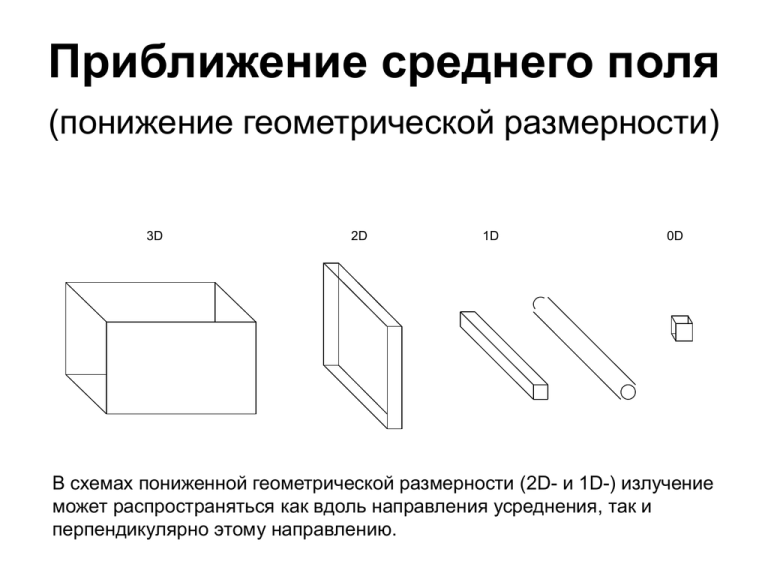
Приближение среднего поля
(понижение геометрической размерности)
3D
2D
1D
0D
В схемах пониженной геометрической размерности (2D- и 1D-) излучение
может распространяться как вдоль направления усреднения, так и
перпендикулярно этому направлению.
Нелинейный слой
(тепловая нелинейность)
d
1
T  T   T dz
d0
2D
 2T  2T
 T  2  2
x
y
 0cv
T
  T  F (T )
t
F (T )   P(T ) I in  H (T  Tm )
1  R0
2h
P(T ) 
1  exp(  (T )d ) , H 
d
d
При
 d  1
доля поглощенной мощности
P(T )  (1  R0 ) (T )
1D, 0D
T
 2T
0cv
  2  F1 (T )
t
x
1D:
0D:
dT
 0cv
  F0 (T )
dt
T  T 
1
T  T 
V
Неподвижные точки – стационарные режимыT
(баланс выделения тепла и теплоотвода)

F0 ()  0
1
T dy dz

S S
 T dx dy dz
V
0D
Условие устойчивости стационарных режимов
Условие баланса тепла
dF0
( )  0
dT
H
I in 
(  Tm )
P()
P() 
H
(  Tm )
I in
Условия бистабильности (мультистабильности) (рис.)
- Наличие точки перегиба функции P(T)
- Температура окружающей среды
d 2 P / dT 2  0
Tm  T *
- Диапазон интенсивности падающего излучения
Бистабильность и гистерезис
Время установления стационарного режима
Критическое замедление
Шумы
I min  I in  I max
Рис.
1D, стационарные режимы
Замена обозначения
F1  F
d2X
m 2  F(X )
dt
d 2T
 2  F (T )
dx
Механическая аналогия
Уравнение теплопроводности
Механическое уравнение Ньютона
Коэффициент
теплопроводности
Λ
Масса
m
Температура
T
Координата
X
Координата
x
Время
t
Баланс тепла
F(T)
Сила
F(X)
Механическая аналогия
«Потенциальная энергия»
T
U    F (T ) dT
U  A(T ) I in  B(T )
T
H
A(T )   P(T ) dT , B(T )  (T  Tm ) 2  const
2
Аналог закона сохранения механической энергии
  dT 

  U (T )  W  const
2  dx 
2
Рис.
Волны переключения
НУШ: от (1 + 2) к (1 + 1)
Нелинейный планарный волновод
 E 1 E 
 2 E
2ik0 

   E  D2

2
 z v t 
t
g


k02 
1  P 
 4   P  2i
  0.
0 
0 t 
Пучки монохроматического излучения, поляризация фиксирована
E
k02
2ik0
   E  4  P  0
z
0
Керровская нелинейность; (1 + 2) НУШ
E  2 E  2 E 02
2ik0
 2  2  2  2 | E |2 E  0
z x
y
c
Понижение размерности
Планарный волновод одномодовый по направлению y. Приближенная факторизация
E( x, y, z)  F ( y) A( x, z)
A
2 A
 2 F 02
2ik0 F
 F 2  A 2  2  2 | F |2 F | A |2 A  0
z
x
y
c
Домножаем наF
*
( y)
и интегрируем по y



2
2

A  2 A 

F

2
*
2
4
0
2
ik

|
F
(
y
)
|
dy

A
F
(
y
)
dy


|
A
|
A
|
F
(
y
)
|
dy  0
 0 z x 2  
2
2 2


y
c

 


Планарный волновод


2F
F
*
 F ( y ) y 2 dy   F ( y ) d y 
*
F
 F *( y)
y







2
2
F
F
dy   
dy   s,
y
y

s  const  0.


A  2 A 
 2 
 2ik0
z x 

s
A

2
|
F
(
y
)
|
dy

02
c
2
4
|
F
(
y
)
|
dy

 2 | A |2 A 


0
2
|
F
(
y
)
|
dy


A( x, z)  B( x, z)exp(i k  z )

1
k 
2k0
s

2
|
F
(
y
)
|
dy


1

2k0



2
|
F
(
y
)
|
dy



2
F
dy
y
0
4
|
F
(
y
)
|
dy

 2   2 

2
|
F
(
y
)
|
dy


(1+1)-НУШ
Сдвиг постоянной распространения в волноводе по сравнению со сплошной средой.
B  2 B 02
2ik0
 2  2  2 | B |2 B  0
z x
c
(1 + 1) НУШ
Аналогично
Одномодовый световод
НУШ в безразмерном виде
E   2 E
2
i


|
E
|
E 0
2
z 2 
  1
Резонаторные схемы
(лазер с насыщающимся поглощением и нелинейный интерферометр)
Квазиоптическое приближение, фиксированная поляризация
Ein  Re{Ein (r , z, t ) exp[i(k0 z  0t )]}, z  0
E  Re{E (r , z, t ) exp[i(km z  0t )]}, 0  z  d
ˆ E (r , 0, t   ),   d / v
E (r , d , t )  M

d
d
g
 E 1 E 
02
2E
2ikm 

   E  D2 2  4 2  P  0
 z v t 
t
c
g


Рис.
Линейные элементы
Линейные (вакуумные) промежутки длины L
ˆ E(r , d , t  ),   L / v
E(r , d  L, t )  M

L
L
L
 E 1 E 
2ikL 

   E  0
 z vL t 
ˆ E(r , z , t  ( z  z ) / v )
E(r , z2 , t )  D
 1
2
1
L
 i 
E (r , z2 , t )  [L ( z2  z1 )] m / 2 exp  

 2m 
 ik L (r  r ) 2  
z2  z1 

 exp 
E
r
,
z
,
t

 dr
   1
vL 
 2( z2  z1 )  
m =1 (поперечно одномерная геометрия, щелевые пучка) и 2 (поперечно-двумерная геометри
Апертурное ограничение
ˆ
Eout (r , z, t )  AEin (r , z, t )
Зеркало с амплитудным (комплексным) коэффициентом отражения R и апертурным ограничен
ˆ E (r , z, t )
Eout (r , z, t )  RA
in 
Кривизна зеркала включается в координатную зависимость
Пространственный фильтр
k
Для пространственного фильтра плотность амплитуды на пространственной частоте
G (k  ) 

1
(2 )
m
E
in
(r ) exp(ik r ) dr

Диафрагма в фокальной плоскости отсекает компоненты поля с пространственными частотами >
Eout (r )  Fˆ Ein (r ) 

qf
dk G (k  ) exp( ik r ) 
k  q f
На выходе фильтра


k  q f
dk  exp( ik r )  dr Ein (r) exp(ik r )
Fˆ  1ˆ
В отсутствие диафрагмыq(f  ) оператор пространственной фильтрации единичный,
В телескопической системе с различающимися фокусными расстояниями линз
происходит изменение масштаба с коэффициентом увеличения η:
ˆ E (r )  E (r )
Eout (r )  T
in 
in

Область входного зеркала
На линейном участке вблизи входного зеркала происходит когерентное
сложение полей внешнего и циркулирующего внутри интерферометра
излучения. Ввиду существенности при этом фазовых соотношений этот
этап описывается сложением полных (быстро меняющихся) амплитуд
E (r ,0, t )  Ein (r ,0, t )  R0 E (r , L, t   in )
Ein  T0 Ein
ˆ ˆ E (r ,0, t   )
E (r ,0, t )  Ein (r ,0, t )  Rexp(i ph )LM

r
Вид оператора преобразования поля в нелинейной среде определяется
формой материального уравнения для нелинейной поляризации среды или
нелинейной диэлектрической проницаемости. Для многих задач достаточно
использовать релаксационное уравнение с диффузией

1
   [   nl (| E |2 )]  D
t
 rel

1



[   nl (| E |2 )]
В пренебрежении диффузиейt
 rel
   nl (| E | )
В пренебрежении конечностью времени релаксации (мгновенная нелинейность)
2
Усреднение по продольному направлению
d
1
 E   E dz
d0
Условия применимости
| E   E || E |
1  R  1, 2ph  1, L  Ld ,
d  lnl
В отсутствие линейных элементов внутри интерферометра с использованием граничного усло
(знак усреднения опущен)
1 E
i
D2  2 E

E  i

2
vg t 2km
2km t
i
2 km
m
1
d
 P  {[1  R exp(i ph )]E  Ein }  0
При наличии плавной фильтрации
 i
i
1 R 

E   
 2   E


2k m
 2km q ph d

Галилеевское преобразование
D2  0
Безынерционная нелинейность и не зависящая от одной из поперечных координат (x) амплитуда
падающего излучения. Галилеевское преобразование:
Падающее излучение
Поле в интерферометре
Ein(0) ( y , t )
E (0) ( y , t )
Ein(0) ( y , t ) exp(ik ) exp( i t )
E (0) ( x  Vt , y , t ) exp(ik ) exp( i t )
V  vg ,  
vg 2
2k m
Модуляционная неустойчивость.
Пороговая нелинейность.
Лазерные схемы. Опасность бесконечных размеров (усиленное спонтанное
излучение). Лазер с насыщающимся поглощением
Ударные электромагнитные волны
Немагнитная среда (μ = 1, B = H) без свободных зарядов и токов.
Поглощение и дисперсия отсутствуют. Тогда индукция D(t) в каждой точке
определяется значением напряженности электрического поля E(t) (это
полное поле, не огибающая)
1 D
1 H
rot H 
, rot E 
c t
c t
Другие дифференциальные уравнения Максвелла не понадобятся, так как
рассматриваются плоские волны, распространяющиеся вдоль оси z, так что
все величины зависят только от z и t. Полагаем, что отличны от нуля только
следующие компоненты векторов:
Ex  E , Dx  D  D( E ), H y  H
При этом
div E  div H  0
1D-уравнения Максвелла

H 1 D  E
E 1 H
=

, 
=
z c t c t
z c t
   (E) 
dD
dE
- эффективная диэлектрическая проницаемость
В пределе слабого поляE  0
ε переходит в линейную диэлектрическую проницаемость
 0   (0)
Ударные волны
Ищем не общее, а специальное решение 1D-уравнений Максвелла, в котором
напряженность магнитного поля Н(z, t) однозначно выражается через
напряженность электрического поля Е(z, t), так что Н = Н(Е). Сама эта
зависимость будет найдена далее. Тогда в уравнениях Максвелла можно перейти
к единственной неизвестной функции
 E
dH E
1 dH E E

 0,

0
c t dE z
c dE t z
Система линейных алгебраических уравнений относительно
E / t
и
E / z
Ввиду однородности системы она разрешима (для ненулевых решений),
только если ее определитель равен нулю
2
 dH 

   (E)
 dE 
Уравнение переноса
E
H     ( E ) dE  const
общее решение

E  f z


E
 E

0
z
c t

c
t
 ( E ) 
Два знака отвечают направлениям распространения волны в положительном или
отрицательном направлении оси z. В слабых полях это решение переходит в обычную
c / с0 фазовой скоростью
плоскую волну
В низкочастотной области  ( E ) убывает. Тогда точки профиля импульса с большей напряженностью
Е бегут с б’ольшими скоростями, так что крутизна переднего фронта импульса увеличивается по
мере его распространения (рис.) В некоторый момент касательная к профилю импульса в какой-то
точке переднего импульса становится вертикальной, после чего формально зависимость E(z) при t =
const становится неоднозначной. Это отвечает возникновению ударной электромагнитной волны. В
действительности рассмотрение оправдано только до момента возникновения разрыва, так как по
мере увеличения крутизны фронта импульса его спектр расширяется и существенными становятся
не учитывавшиеся в анализе дисперсия и поглощение среды.
Предельно сильные поля
Предельно короткие импульсы (аттосекундные)
Квантовая и статистическая нелинейная оптика