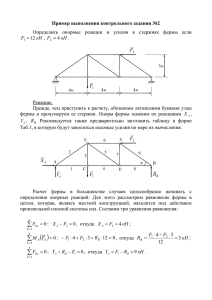
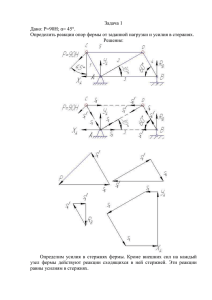
Пример определения усилий в стержнях ферм методом

ПРИМЕР РАСЧЕТА
F1=2кН
a
a
a
a
F2=5кН
Необходимо определить усилия во всех стержнях фермы.
Размеры и приложенная к ферме нагрузка указаны на чертеже.
ПРИМЕР РАСЧЕТА
F1=2кН G
2
A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН
Прежде всего необходимо обозначить все
узлы фермы и пронумеровать все стержни
ПРИМЕР РАСЧЕТА
F1=2кН G
2
A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН
Полный расчёт фермы, при котором необходимо определить
усилия во всех стержнях, имеет смысл начать с определения
реакций опор. Для этого рассматривается равновесие всей фермы.
ПРИМЕР РАСЧЕТА
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР ФЕРМЫ
F1=2кН G
2
A
5
3
1
a
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН
Выбор формы условий равновесия зависит от количества и
расположения опор. Нужно составлять уравнения таким образом,
чтобы из каждого уравнения определялась одна составляющая
реакций опор.
ПРИМЕР РАСЧЕТА
F1=2кН G
2
1
a
∑ Fkx= 0 :
5
3
XA (-2) A
C
E
6
4
9
7
D
a
8
a
B
a
YA (1)
F2=5кН YB (4)
XA+F1= 0
XA = – F1 = – 2 (кН)
∑ MAz(Fk) = 0 : – F1∙a – F2 ∙2a + YB ∙3a = 0
2∙1 + 5 ∙2 4
= (кН)
3
YA = F2 – YB = 5 – 4= 1(кН)
1
YA – F2 + YB= 0
YB =
∑ Fky= 0 :
ПРИМЕР РАСЧЕТА
F1=2кН G
2
1
a
∑ Fkx= 0 :
5
3
XA (-2) A
C
E
6
4
9
7
D
a
8
a
B
a
YA (1)
F2=5кН YB (4)
XA+F1= 0
XA = – F1 = – 2 (кН)
∑ MAz(Fk) = 0 : – F1∙a – F2 ∙2a + YB ∙3a = 0
2∙1 + 5 ∙2 4
= (кН)
3
YA = F2 – YB = 5 – 4= 1(кН)
1
YA – F2 + YB= 0
YB =
∑ Fky= 0 :
ПРИМЕР РАСЧЕТА
F1=2кН G
2
XA (-2) A
a
YA (1)
5
3
1
C
E
6
4
9
7
D
a
8
a
B
a
F2=5кН YB (4)
Проверка:
Для проверки правильности полученных результатов
составим уравнение моментов относительно такой точки,
относительно которой все вычисленные силы реакций
создают ненулевые моменты.
ПРИМЕР РАСЧЕТА
F1=2кН G
2
XA (-2) A
a
YA (1)
5
3
1
C
E
6
4
9
7
D
a
8
a
B
a
F2=5кН YB (4)
Проверка:
∑ MЕz(Fk) = XA∙a – YA ∙2a + YB ∙a = –2∙a – 1 ∙2a + 4 ∙a = 0
ПРИМЕР РАСЧЕТА
F1=2кН G
2
XA (-2) A
a
YA (1)
5
3
1
C
E
6
4
9
7
D
a
8
a
B
a
F2=5кН YB (4)
Проверка:
∑ MЕz(Fk) = XA∙a – YA ∙2a + YB ∙a = –2∙a – 1 ∙2a + 4 ∙a = 0
ПРИМЕР РАСЧЕТА
F1=2кН G
МЕТОД ВЫРЕЗАНИЯ УЗЛОВ
2
XA (-2) A
a
YA (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
Метод вырезания узлов состоит в том, что рассматривается
равновесие каждого узла.
ПРИМЕР РАСЧЕТА
F1=2кН G
На каждый узел дей2
3
ствует плоская система
XA (-2) A
сходящихся сил, состоя1 C
щая из приложенных к
a
данному узлу активных
сил и реакций стержней,
YA (1)
присоединённых к данному узлу.
Для такой системы сил можно
составить только два уравнения
равновесия:
∑ Fkx= 0;
∑ Fky= 0 .
E
6
5
9
7
D
4
a
8
a
B
a
F2=5кН YB (4)
F1
S2
G
S3
S6
S5
Поэтому равновесие узлов нужно рассматривать в определённой
последовательности, позволяющей на каждом шаге решения задачи
определять две очередные неизвестные.
ПРИМЕР РАСЧЕТА
F1=2кН G
На каждый узел дей2
3
ствует плоская система
XA (-2) A
сходящихся сил, состоя1 C
щая из приложенных к
a
данному узлу активных
сил и реакций стержней,
YA (1)
присоединённых к данному узлу.
Для такой системы сил можно
составить только два уравнения
равновесия:
∑ Fkx= 0;
∑ Fky= 0 .
E
6
5
9
7
D
4
a
8
a
B
a
F2=5кН YB (4)
F1
S2
G
S3
S6
S5
Поэтому равновесие узлов нужно рассматривать в определённой
последовательности, позволяющей на каждом шаге решения задачи
определять две очередные неизвестные.
ПРИМЕР РАСЧЕТА
F1=2кН G
На каждый узел дей2
3
ствует плоская система
XA (-2) A
сходящихся сил, состоя1 C
щая из приложенных к
a
данному узлу активных
сил и реакций стержней,
YA (1)
присоединённых к данному узлу.
E
6
5
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
Для такой системы сил можно
составить только два уравнения
равновесия:
∑ Fkx= 0;
∑ Fky= 0 .
; узлов нужно рассматривать в определённой
Поэтому равновесие
последовательности, позволяющей на каждом шаге решения задачи
определять две очередные неизвестные.
ПРИМЕР РАСЧЕТА
F1=2кН G
2
XA (-2) A
Правило знаков:
a
YA (1)
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
«+» – растягивающие усилия
(направлены от узла);
«–» – сжимающие усилия.
Изначально при расчете все усилия предполагаются
положительными и направляются от узлов.
ПРИМЕР РАСЧЕТА
Узел В:
F1=2кН G
y
S9
S8
2
450
XA (-2) A
B
x
YB = 4
∑ Fkx= 0 : –S8 – S9 cos
0
45
∑ Fky= 0 : YB + S9 sin
450
a
YA (1)
=0;
=0.
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
ПРИМЕР РАСЧЕТА
Узел В:
F1=2кН G
y
S9
S8
2
450
XA (-2) A
B
x
YB = 4
∑ Fkx= 0 : –S8 – S9 cos
0
45
∑ Fky= 0 : YB + S9 sin
0
45Y
B
=
0
sin 45
a
YA (1)
=0;
=0.
4
= – 4√2 (кН);
√2/2
√2
0
=
4√2∙
= 4 (кН).
(1) => S8 = – S9 cos 45
2
(2) => S9 =
5
3
1
C
E
6
4
a
9
7
D
8
a
B
a
F2=5кН YB (4)
ПРИМЕР РАСЧЕТА
Узел В:
F1=2кН G
y
S9
S8
2
450
XA (-2) A
B
x
∑ Fkx= 0 : –S8 – S9 cos
0
45
∑ Fky= 0 : YB + S9 sin
C
a
YB = 4
5
3
1
E
6
4
9
7
D
a
a
B
8
a
F2=5кН YB (4)
YA (1)
=0;
=0.
0
45Y
B
=
sin 450
4
= –– 4√2
4√2 (кН);
√2/2
√2
= 44 (кН).
(1) => S8 = – S9 cos 450 = 4√2∙
2
(2) => S9 =
№ стержня
Усилие, кН
1
2
3
4
5
6
7
8
9
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел В:
Е:
F1=2кН G
y
S9
S8
2
450
XA (-2) A
B
x
∑ Fkx= 0 : –S8 – S9 cos
0
45
∑ Fky= 0 : YB + S9 sin
C
a
YB = 4
5
3
1
E
6
4
9
7
D
a
a
B
8
a
F2=5кН YB (4)
YA (1)
=0;
=0.
0
45Y
B
=
sin 450
4
= – 4√2 (кН);
√2/2
√2
= 4 (кН).
(1) => S8 = – S9 cos 450 = 4√2∙
2
(2) => S9 =
№ стержня
Усилие, кН
1
2
3
4
5
6
7
8
9
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел Е:
F1=2кН G
E
6
y
2
E
S6
S7
XA (-2) A
x
450
1
C
a
S9 = – 4√2
5
3
9
7
D
4
a
a
B
8
a
F2=5кН YB (4)
YA (1)
√2
∑ Fkx= 0 : –S6 + S9 cos 450 = 0 => S6 = S9 cos 450 = – 4√2∙ 2 = – 4 (кН);
√2
∑ Fky= 0 : – S7 – S9 sin 450 = 0 => S7 = – S9 sin 450 = 4√2∙ 2 = 4 (кН).
№ стержня
Усилие, кН
1
2
3
4
5
6
7
8
9
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел D
Е:
F1=2кН G
E
6
y
2
E
S6
S7
XA (-2) A
x
450
5
3
1
C
D
4
a
S9 = – 4√2
9
7
a
B
8
a
a
F2=5кН YB (4)
YA (1)
√2
∑ Fkx= 0 : –S6 + S9 cos 450 = 0 => S6 = S9 cos 450 = – 4√2∙ 2 = – 4 (кН);
√2
∑ Fky= 0 : – S7 – S9 sin 450 = 0 => S7 = – S9 sin 450 = 4√2∙ 2 = 4 (кН).
№ стержня
Усилие, кН
1
2
3
4
5
6
7
8
9
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел D :
F1=2кН G
y
S5
S7 = 4
450
S4
2
XA (-2) A
D
S8 = 4
x
∑ Fky= 0 : S5 sin
450 +
C
a
F2 = 5
5
3
1
E
6
4
a
B
8
a
F2=5кН YB (4)
F2 – S7
sin
D
a
YA (1)
S7 – F2 = 0 => S5 =
9
7
450
= (5 – 4)√2 = √2 (кН);
√2
∑ Fkx= 0 : – S4 – S5 соs 450 + S8 = 0 => S4 = – S5 соs 450 + S8 = – √2 2 + 4 = 3
(кН)
№ стержня
Усилие, кН
1
2
3
4
5
6
7
8
9
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел
Узел D
C:
F1=2кН G
y
S5
S7 = 4
450
S4
2
XA (-2) A
D
S8 = 4
x
∑ Fky= 0 : S5 sin
450 +
C
a
F2 = 5
5
3
1
E
6
4
a
B
8
a
F2=5кН YB (4)
F2 – S 7
sin
D
a
YA (1)
S7 – F2 = 0 => S5 =
9
7
450
= (5 – 4)√2 = √2 (кН);
√2
∑ Fkx= 0 : – S4 – S5 соs 450 + S8 = 0 => S4 = – S5 соs 450 + S8 = – √2 2 + 4 = 3
(кН)
№ стержня
Усилие, кН
1
2
3
4
5
6
7
8
9
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел С :
F1=2кН G
y
2
S3
XA (-2) A
С
S1
S4 = 3
C
a
x
5
3
1
E
6
4
9
7
D
a
a
B
8
a
F2=5кН YB (4)
YA (1)
∑ Fkx= 0 : – S1 + S4 = 0 => S1 = S4 = 3 (кН)
;
∑ Fky= 0 :
S3 = 0.
0
№ стержня
1
Усилие, кН
3
2
3
4
5
6
7
8
9
0
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел С
А::
F1=2кН G
y
2
S3
XA (-2) A
С
S1
S4 = 3
C
a
x
5
3
1
E
6
4
9
7
D
a
a
B
8
a
F2=5кН YB (4)
YA (1)
∑ Fkx= 0 : – S1 + S4 = 0 => S1 = S4 = 3 (кН)
;
∑ Fky= 0 :
S3 = 0.
0
№ стержня
1
Усилие, кН
3
2
3
4
5
6
7
8
9
0
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел А:
F1=2кН G
E
6
y
S2
А
2
XA (-2) A
450
S1 = 3
XA =–2
a
YA = 1
∑ Fky= 0 : S2 sin
450 +
C
1
x
5
3
4
YA = 0 => S2 = –
sin
450
D
a
a
B
8
a
F2=5кН YB (4)
YA (1)
YA
9
7
= –√2
√2 (кН).
№ стержня
1
2
3
4
5
6
7
8
9
Усилие, кН
3
– √2
0
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел А:
F1=2кН G
E
6
y
S2
А
2
XA (-2) A
450
S1 = 3
XA =–2
a
YA = 1
∑ Fky= 0 : S2 sin
450 +
C
1
x
5
3
4
YA = 0 => S2 = –
sin
450
D
a
a
B
8
a
F2=5кН YB (4)
YA (1)
YA
9
7
= –√2 (кН).
Проверка
∑ Fkx= XA + S1 + S2 sin 450 =
Узел А:
= –2 + 3 –√2
√2
=0
2
№ стержня
1
2
3
4
5
6
7
8
9
Усилие, кН
3
– √2
0
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
Узел А:
F1=2кН G
E
6
y
S2
А
2
XA (-2) A
450
S1 = 3
XA =–2
a
YA = 1
∑ Fky= 0 : S2 sin
450 +
C
1
x
5
3
4
YA = 0 => S2 = –
sin
450
D
a
a
B
8
a
F2=5кН YB
YA (1)
YA
9
7
= –√2 (кН).
Проверка
∑ Fkx= XA + S1 + S2 sin 450 =
Узел А:
= –2 + 3 –√2
√2
=0
2
№ стержня
1
2
3
4
5
6
7
8
9
Усилие, кН
3
– √2
0
3
√2
–4
4
4
– 4√2
ПРИМЕР РАСЧЕТА
F1=2кН G
Проверка
Узел А:
2
∑ Fkx= XA + S1 + S2 sin 450 =
= –2 + 3 –√2
Узел G:
F1 = 2
XA (-2) A
√2
=0
2
5
3
1
C
a
E
6
4
S2 = –√2
B
8
a
F2=5кН YB
= 2 – 4 + √2∙
x
450
a
∑ Fkx= F1 + S6 – S2 cos450 + S5 cos450 =
G S6 = – 4
450
D
a
YA (1)
y
9
7
√2
√2
+ √2∙
=0
2
2
∑ Fky= – S2 sin450 – S5 sin450 =
S5 = √ 2
S3 = 0
= √2∙
√2
√2
=0
– √2∙
2
2
№ стержня
1
2
3
4
5
6
7
8
9
Усилие, кН
3
– √2
0
3
√2
–4
4
4
– 4√2