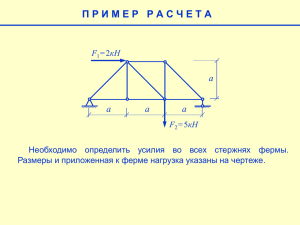
Статика. Определение реакций опор и усилий
реклама
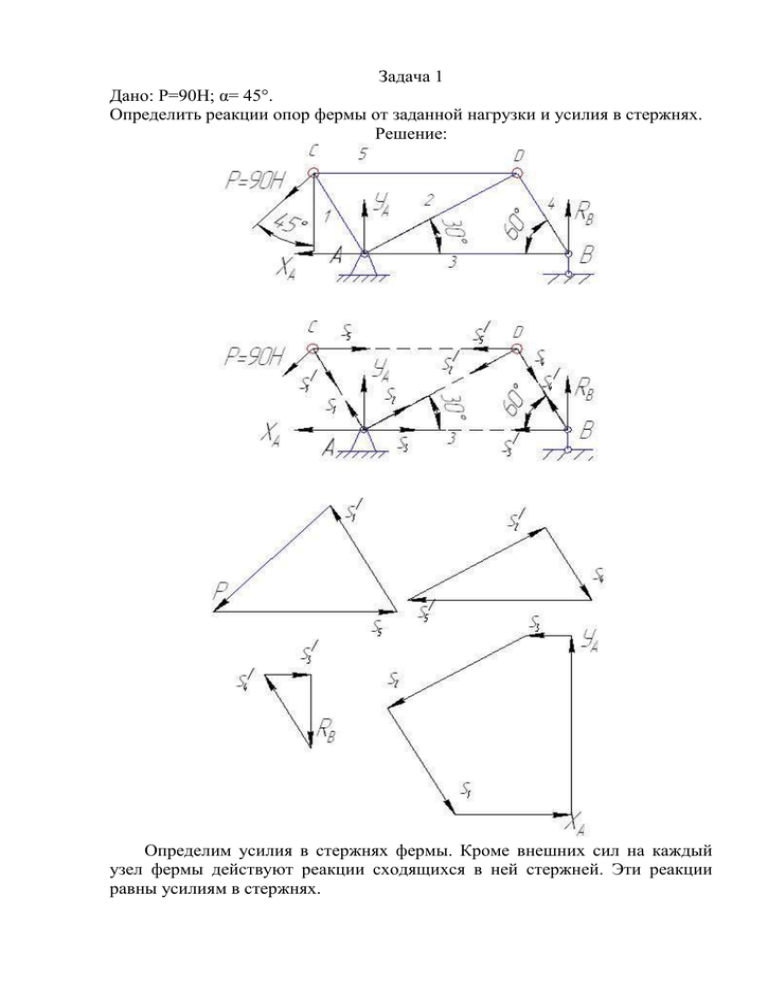
Задача 1 Дано: Р=90Н; α= 45°. Определить реакции опор фермы от заданной нагрузки и усилия в стержнях. Решение: Определим усилия в стержнях фермы. Кроме внешних сил на каждый узел фермы действуют реакции сходящихся в ней стержней. Эти реакции равны усилиям в стержнях. Рассмотрим равновесия сил приложенных к каждому узлу фермы, выбирая узлы в такой последовательности, чтобы число неизвестных сил в узле не превышало двух. Расчет начнем с узла С Составим уравнения равновесия сил, приложенных к этому узлу: Fkx 0 S1 cos 60 S5 P cos 45 0 Fky 0 S1 sin 60 P sin 45 0 S1 P sin 45 73.48 H sin 60 S 5 S1 cos 60 P cos 45 100,38H Стержень 5 растянут, а стержень 1 сжат. Для проверки расчета строим в масштабе треугольник сил. Треугольник сил получается замкнутым, следовательно, реакции определены правильно. Реакции остальных стержней определим аналогично. Расчет узла D Составим уравнения равновесия сил, приложенных к этому узлу: Fkx 0 S 2 cos 30 S5 S 4 cos 60 0 Fky 0 S2 sin 30 S4 sin 60 0 S 2 86,93H S4 S 2 sin 30 50,18 Н sin 60 Стержень 4 растянут, а стержень 2 сжат. Расчет узла B Составим уравнения равновесия сил, приложенных к этому узлу: Fkx 0 S 4 cos 60 S3 0 Fky 0 S4 sin 60 RB 0 S 3 S 4 cos 60 25.09H RB S 4 sin 60 43.45H Стержень 3 сжат, реакция RB направлена противоположно показанной на рисунке. Расчет узла А Составим уравнения равновесия сил, приложенных к этому узлу: Fkx 0 Х А S1 cos 60 S3 S 2 cos 30 0 Fky 0 У А S1 sin 60 S2 sin 30 0 Х А S1 cos 60 S 3 S 2 cos 30 63.63H У А S1 sin 60 S 2 sin 30 107.1H Реакция Х А направлена противоположно показанной на рисунке.