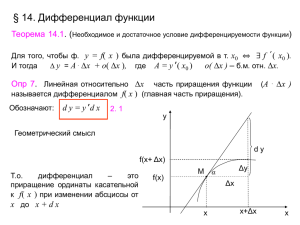
Дифференциал функции
реклама

Дифференциал Понятие о дифференциале функции. Определение: Дифференциалом функции называется величина, пропорциональная приращению независимой переменной и отличающаяся от приращения функции на бесконечно малую функцию высшего порядка малости по сравнению с приращением независимой переменной. Связь дифференциала функции с производной. Дифференциал независимой переменной. Теорема 1. Если функция имеет дифференциал, то эта функция имеет производную. Следствие: dy = y x x. Теорема 2. Если функция имеет производную, то эта функция имеет дифференциал. Определение. Под дифференциалом независимой переменной понимается дифференциал функции, тождественной с независимой переменной, т.е. при y = x. y= 1, то dy = dx =.x dy Следствие: dy = y x dx; y x dx . Свойства дифференциала. Предполагаем, что функции дифференцируемы 1.dc = 0; 2.d(u+c) = du; 3.d(u+v-w) = du+dv-dw; 4.d(cu) = cdu; 5.d(uv) = vdu + udv; 6.d vdu udv = u ; 2 v v 7.Дифференциал сложной функции. y = f((x)); y = f(u); u = ((x); yx = yu ux dx yxdx = yu(uxdx) dy = yu uxdx dy du dy = yudu – эта формула совпадает по форме с dy = yxdx, но есть и принципиальное отличие x x t y y t в x xt x – независимая переменная и x dx; y y t а в dy = yudu u есть функция du .u Из функции dy = yudu Независимость вида дифференциала от выбора независимой переменной. ! Дифференциал функции = произведению производной этой функции на дифференциал аргумента, при этом аргумент может быть как независимой переменной, так и дифференцируемой функцией от другой независимой переменной. Таблица дифференциалов функций 1.dun = nun-1du 2.dan = an lnadu 3.den - endu du 4.d(logau) = u ln a 5.d (sinu) = cosudu 6.d(cosu) = -sinudu du 7.d(tgu) = 2 cos u du 8.d(ctgu) = - 2 sin u 9.d(arcsinu) = du 1 u2 du 10.d(arccosu) = - 1 u2 du 11.d(arctgu) = 1 u2 du 12.d(arcctgu) = 2 1 u 13.df(u) = f(u)du. Приближенные вычисления с помощью дифференциала. y =f(x); x; x+ x D(y); y дифференцируема y y ( x) x 0 (x) y yx x dy; yx x yx yx x. Дифференциалы высших порядков. y =f(x); x – независимая переменная, f(x) – дифференцируемая функция. d f(x) = f(x)dx. Определение. Дифференциалом второго порядка d2f(x) функции y =f(x) называется дифференциал от дифференциала первого порядка этой функции. d f x d df x . 2 dx – const, dy – функция x. d 2 f x d f x dx dx df x dx f x2 dx f x2 dx 2 .